scipy.interpolate.

CubicSpline#

class scipy.interpolate.CubicSpline(x, y, axis=0, bc_type='not-a-knot', extrapolate=None)[Quelle]#

Stückweiser kubischer Interpolator zur Anpassung von Werten (C2-glatt).

Interpoliert Daten mit einem stückweisen kubischen Polynom, das zweimal stetig differenzierbar ist [1]. Das Ergebnis wird als eine PPoly-Instanz mit Knotenpunkten dargestellt, die den gegebenen Daten entsprechen.

Parameter:

xarray_like, Form (n,)

1-D-Array mit den Werten der unabhängigen Variable. Werte müssen reell, endlich und in streng aufsteigender Reihenfolge sein.

yarray_like

Array mit den Werten der abhängigen Variable. Es kann beliebig viele Dimensionen haben, aber die Länge entlang der axis (siehe unten) muss der Länge von x entsprechen. Werte müssen endlich sein.

axisint, optional

Achse, entlang der y als variierend angenommen wird. Das bedeutet, dass für x[i] die entsprechenden Werte np.take(y, i, axis=axis) sind. Standard ist 0.

bc_typeString oder 2-Tupel, optional

Typ der Randbedingung. Zwei zusätzliche Gleichungen, gegeben durch die Randbedingungen, sind erforderlich, um alle Koeffizienten der Polynome auf jedem Segment zu bestimmen [2].

Wenn bc_type ein String ist, dann wird die angegebene Bedingung an beiden Enden einer Spline angewendet. Verfügbare Bedingungen sind:

‘not-a-knot’ (Standard): Das erste und zweite Segment an einem Kurvenende sind dasselbe Polynom. Dies ist eine gute Standardeinstellung, wenn keine Informationen über Randbedingungen vorliegen.
‘periodic’: Die interpolierte Funktion wird als periodisch mit der Periode x[-1] - x[0] angenommen. Der erste und letzte Wert von y müssen identisch sein: y[0] == y[-1]. Diese Randbedingung führt zu y'[0] == y'[-1] und y''[0] == y''[-1].
‘clamped’: Die erste Ableitung an den Kurvenenden ist Null. Bei einem 1-D y ist bc_type=((1, 0.0), (1, 0.0)) dieselbe Bedingung.
‘natural’: Die zweite Ableitung an den Kurvenenden ist Null. Bei einem 1-D y ist bc_type=((2, 0.0), (2, 0.0)) dieselbe Bedingung.

Wenn bc_type ein 2-Tupel ist, werden der erste und der zweite Wert am Anfang bzw. Ende der Kurve angewendet. Die Tupelwerte können einer der zuvor genannten Strings sein (außer ‘periodic’) oder ein Tupel (order, deriv_values), das die Angabe beliebiger Ableitungen an den Kurvenenden ermöglicht.

order: die Ordnung der Ableitung, 1 oder 2.
deriv_value: Array-ähnlich mit den Ableitungswerten, die Form muss dieselbe sein wie bei y, die Achsendimension ausgenommen. Wenn y beispielsweise 1-D ist, muss deriv_value ein Skalar sein. Wenn y 3-D mit der Form (n0, n1, n2) und axis=2 ist, muss deriv_value 2-D sein und die Form (n0, n1) haben.

extrapolate{bool, ‘periodic’, None}, optional

Wenn bool, bestimmt, ob für Punkte außerhalb des Bereichs basierend auf dem ersten und letzten Intervall extrapoliert wird oder NaNs zurückgegeben werden. Wenn ‘periodic’, wird periodische Extrapolation verwendet. Wenn None (Standard), wird extrapolate für bc_type='periodic' auf ‘periodic’ und andernfalls auf True gesetzt.

Attribute:

xndarray, Form (n,): Knotenpunkte. Dieselben x, die an den Konstruktor übergeben wurden.
cndarray, Form (4, n-1, …): Koeffizienten der Polynome auf jedem Segment. Die nachgestellten Dimensionen entsprechen den Dimensionen von y, die Achse ausgenommen. Wenn beispielsweise y 1-D ist, ist c[k, i] ein Koeffizient für (x-x[i])**(3-k) auf dem Segment zwischen x[i] und x[i+1].
axisint: Interpolationsachse. Dieselbe Achse, die an den Konstruktor übergeben wurde.

Methoden

`__call__`(x[, nu, extrapolate])	Evaluiere das stückweise definierte Polynom oder seine Ableitung.
`derivative`([nu])	Erstelle ein neues stückweise definiertes Polynom, das die Ableitung darstellt.
`antiderivative`([nu])	Erstelle ein neues stückweise definiertes Polynom, das die Stammfunktion darstellt.
`integrate`(a, b[, extrapolate])	Berechne ein bestimmtes Integral über ein stückweise definiertes Polynom.
`solve`([y, discontinuity, extrapolate])	Findet reelle Lösungen der Gleichung `pp(x) == y`.
`roots`([discontinuity, extrapolate])	Reelle Wurzeln des stückweisen Polynoms finden.

Siehe auch

Akima1DInterpolator: Akima 1D-Interpolator.
PchipInterpolator: PCHIP 1D monotoiner kubischer Interpolator.
PPoly: Stückweises Polynom in Bezug auf Koeffizienten und Knotenpunkte.

Hinweise

Die Parameter bc_type und extrapolate arbeiten unabhängig voneinander, d.h. ersteres steuert nur den Aufbau einer Spline und letzteres nur die Auswertung.

Wenn eine Randbedingung ‘not-a-knot’ ist und n = 2, wird sie durch die Bedingung ersetzt, dass die erste Ableitung gleich der Steigung des linearen Interpolanten ist. Wenn beide Randbedingungen ‘not-a-knot’ und n = 3 sind, wird die Lösung als eine Parabel gesucht, die durch die gegebenen Punkte verläuft.

Wenn die Randbedingung ‘not-a-knot’ an beiden Enden angewendet wird, ist die resultierende Spline dieselbe wie die von splrep (mit s=0) und InterpolatedUnivariateSpline zurückgegebene, aber diese beiden Methoden verwenden eine Darstellung in der B-Spline-Basis.

Hinzugefügt in Version 0.18.0.

Referenzen

[1]

Kubische Spline-Interpolation auf Wikiversity.

[2]

Carl de Boor, „A Practical Guide to Splines“, Springer-Verlag, 1978.

Beispiele

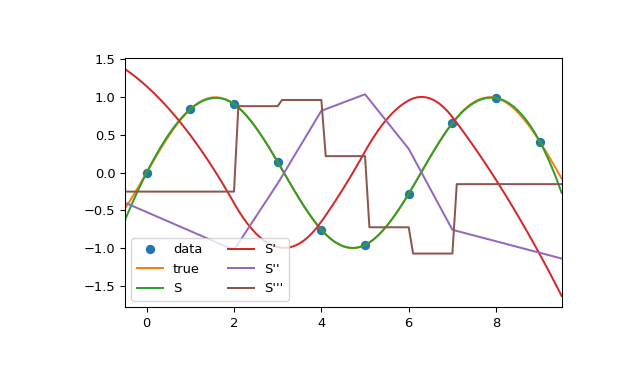
In diesem Beispiel wird die kubische Spline zur Interpolation einer abgetasteten Sinusoidale verwendet. Sie können sehen, dass die Stetigkeitseigenschaft der Spline für die erste und zweite Ableitung gilt und nur für die dritte Ableitung verletzt wird.

>>> import numpy as np
>>> from scipy.interpolate import CubicSpline
>>> import matplotlib.pyplot as plt
>>> x = np.arange(10)
>>> y = np.sin(x)
>>> cs = CubicSpline(x, y)
>>> xs = np.arange(-0.5, 9.6, 0.1)
>>> fig, ax = plt.subplots(figsize=(6.5, 4))
>>> ax.plot(x, y, 'o', label='data')
>>> ax.plot(xs, np.sin(xs), label='true')
>>> ax.plot(xs, cs(xs), label="S")
>>> ax.plot(xs, cs(xs, 1), label="S'")
>>> ax.plot(xs, cs(xs, 2), label="S''")
>>> ax.plot(xs, cs(xs, 3), label="S'''")
>>> ax.set_xlim(-0.5, 9.5)
>>> ax.legend(loc='lower left', ncol=2)
>>> plt.show()

../../_images/scipy-interpolate-CubicSpline-1_00_00.png

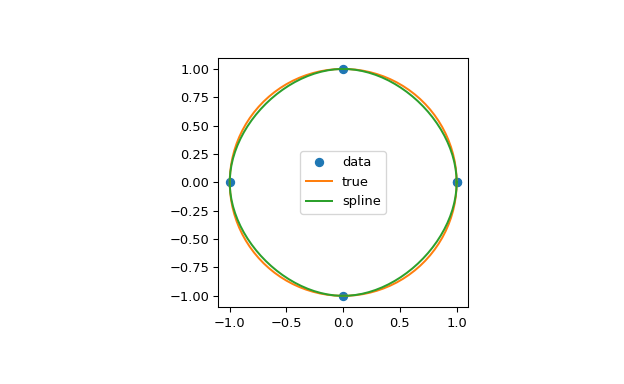
Im zweiten Beispiel wird der Einheitskreis mit einer Spline interpoliert. Es wird eine periodische Randbedingung verwendet. Sie können sehen, dass die Werte der ersten Ableitung, ds/dx=0, ds/dy=1 am periodischen Punkt (1, 0) korrekt berechnet werden. Beachten Sie, dass ein Kreis nicht exakt durch eine kubische Spline dargestellt werden kann. Um die Genauigkeit zu erhöhen, wären mehr Knotenpunkte erforderlich.

>>> theta = 2 * np.pi * np.linspace(0, 1, 5)
>>> y = np.c_[np.cos(theta), np.sin(theta)]
>>> cs = CubicSpline(theta, y, bc_type='periodic')
>>> print("ds/dx={:.1f} ds/dy={:.1f}".format(cs(0, 1)[0], cs(0, 1)[1]))
ds/dx=0.0 ds/dy=1.0
>>> xs = 2 * np.pi * np.linspace(0, 1, 100)
>>> fig, ax = plt.subplots(figsize=(6.5, 4))
>>> ax.plot(y[:, 0], y[:, 1], 'o', label='data')
>>> ax.plot(np.cos(xs), np.sin(xs), label='true')
>>> ax.plot(cs(xs)[:, 0], cs(xs)[:, 1], label='spline')
>>> ax.axes.set_aspect('equal')
>>> ax.legend(loc='center')
>>> plt.show()

../../_images/scipy-interpolate-CubicSpline-1_01_00.png

Das dritte Beispiel ist die Interpolation des Polynoms y = x**3 im Intervall 0 <= x <= 1. Eine kubische Spline kann diese Funktion exakt darstellen. Um dies zu erreichen, müssen wir die Werte und die ersten Ableitungen an den Endpunkten des Intervalls angeben. Beachten Sie, dass y’ = 3 * x**2 und somit y’(0) = 0 und y’(1) = 3.

>>> cs = CubicSpline([0, 1], [0, 1], bc_type=((1, 0), (1, 3)))
>>> x = np.linspace(0, 1)
>>> np.allclose(x**3, cs(x))
True