InterpolatedUnivariateSpline#
- class scipy.interpolate.InterpolatedUnivariateSpline(x, y, w=None, bbox=[None, None], k=3, ext=0, check_finite=False)[Quelle]#
1-D interpolierende Spline für einen gegebenen Satz von Datenpunkten.
Veraltet
Diese Klasse gilt als veraltet und wird keine weiteren Updates mehr erhalten. Obwohl wir derzeit keine Pläne haben, sie zu entfernen, empfehlen wir, dass neuer Code modernere Alternativen verwendet. Insbesondere empfehlen wir die Verwendung von
make_interp_spline.Passt eine Spline y = spl(x) vom Grad k an die bereitgestellten x, y-Daten an. Die Spline-Funktion verläuft durch alle bereitgestellten Punkte. Entspricht
UnivariateSplinemit s = 0.- Parameter:
- x(N,) array_like
Eingabedimension von Datenpunkten – muss streng monoton steigend sein
- y(N,) array_like
Eingabedimension von Datenpunkten
- w(N,) array_like, optional
Gewichte für die Spline-Anpassung. Müssen positiv sein. Wenn None (Standard), sind alle Gewichte 1.
- bbox(2,) array_like, optional
2-Sequenz, die die Grenze des Approximationsintervalls angibt. Wenn None (Standard),
bbox=[x[0], x[-1]].- kint, optional
Grad der glättenden Spline. Muss
1 <= k <= 5sein. Standard istk = 3, eine kubische Spline.- extint oder str, optional
Steuert den Extrapolationsmodus für Elemente, die nicht im Intervall der Knotensequenz liegen.
wenn ext=0 oder „extrapolate“, gib den extrapolierten Wert zurück.
wenn ext=1 oder „zeros“, gib 0 zurück.
wenn ext=2 oder „raise“, löse einen ValueError aus.
Wenn ext=3 oder ‘const’, wird der Grenzwert zurückgegeben.
Der Standardwert ist 0.
- check_finitebool, optional
Ob geprüft werden soll, ob die Eingabearrays nur endliche Zahlen enthalten. Deaktivierung kann die Leistung verbessern, kann aber zu Problemen (Abstürze, Nicht-Terminierung oder unsinnige Ergebnisse) führen, wenn die Eingaben Unendlichkeiten oder NaNs enthalten. Standard ist False.
Methoden
__call__(x[, nu, ext])Bewerte den Spline (oder seine nu-te Ableitung) an den Positionen x.
antiderivative([n])Konstruiere einen neuen Spline, der die Stammfunktion dieses Splines darstellt.
derivative([n])Konstruiere einen neuen Spline, der die Ableitung dieses Splines darstellt.
derivatives(x)Gib alle Ableitungen des Splines an der Stelle x zurück.
Gib die Spline-Koeffizienten zurück.
Gib die Positionen der inneren Knoten des Splines zurück.
Gib die gewichtete Summe der quadrierten Residuen der Spline-Approximation zurück.
integral(a, b)Gib das bestimmte Integral des Splines zwischen zwei gegebenen Punkten zurück.
roots()Gib die Nullstellen des Splines zurück.
Fahre die Spline-Berechnung mit dem gegebenen Glättungsfaktor s und den bei der letzten Aufruf gefundenen Knoten fort.
validate_input
Siehe auch
UnivariateSplineEin geglätteter univariater Spline zur Anpassung an eine gegebene Menge von Datenpunkten.
LSQUnivariateSplineeine Spline, für die die Knoten vom Benutzer ausgewählt werden
SmoothBivariateSplineEin glättender bivariate Spline durch die gegebenen Punkte
LSQBivariateSplineEin bivariate Spline unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung
splrepEine Funktion zum Finden der B-Spline-Darstellung einer 1-D-Kurve
splevEine Funktion zur Auswertung eines B-Splines oder seiner Ableitungen
sprootEine Funktion zum Finden der Nullstellen eines kubischen B-Splines
splintEine Funktion zur Auswertung des bestimmten Integrals eines B-Splines zwischen zwei gegebenen Punkten
spaldeEine Funktion zur Auswertung aller Ableitungen eines B-Splines
Hinweise
Die Anzahl der Datenpunkte muss größer sein als der Spline-Grad k.
Beispiele
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import InterpolatedUnivariateSpline >>> rng = np.random.default_rng() >>> x = np.linspace(-3, 3, 50) >>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50) >>> spl = InterpolatedUnivariateSpline(x, y) >>> plt.plot(x, y, 'ro', ms=5) >>> xs = np.linspace(-3, 3, 1000) >>> plt.plot(xs, spl(xs), 'g', lw=3, alpha=0.7) >>> plt.show()
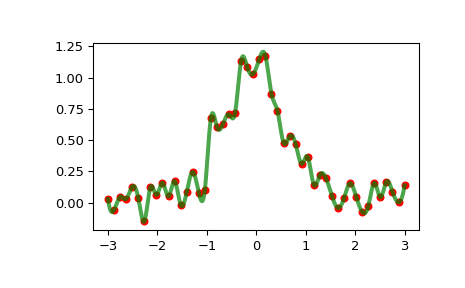
Beachten Sie, dass die
spl(x)y interpoliert>>> spl.get_residual() 0.0