scipy.interpolate.

griddata#

scipy.interpolate.griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)[Quelle]#

Hilfsfunktion zur Interpolation unstrukturierter Daten in mehreren Dimensionen.

Parameter:

points2-D ndarray von floats mit der Form (n, D) oder eine Tupel der Länge D von 1-D ndarrays mit der Form (n,).

Koordinaten der Datenpunkte.

valuesndarray von float oder complex, Form (n,)

Datenwerte.

xi2-D ndarray von floats mit der Form (m, D) oder ein Tupel der Länge D von ndarrays, die auf dieselbe Form broadcastbar sind.

Punkte, an denen Daten interpoliert werden sollen.

method{‚linear‘, ‚nearest‘, ‚cubic‘}, optional

Methode der Interpolation. Eine der folgenden:

nearest: gibt den Wert am Datenpunkt zurück, der dem Interpolationspunkt am nächsten liegt. Siehe NearestNDInterpolator für weitere Details.
linear: tesselliert die Eingabepunktmenge in N-D-Simplizes und interpoliert linear auf jedem Simplex. Siehe LinearNDInterpolator für weitere Details.
cubic (1-D): gibt den Wert zurück, der aus einer kubischen Spline bestimmt wird.
cubic (2-D): gibt den Wert zurück, der aus einer stückweise kubischen, stetig differenzierbaren (C1) und krümmungsminimierenden Polynomfläche bestimmt wird. Siehe CloughTocher2DInterpolator für weitere Details.

fill_valuefloat, optional

Wert, der für angeforderte Punkte außerhalb der konvexen Hülle der Eingabepunkte verwendet wird. Wenn nicht angegeben, ist der Standardwert nan. Diese Option hat keine Auswirkungen auf die Methode ‚nearest‘.

rescalebool, optional

Skaliert die Punkte auf einen Einheitswürfel, bevor die Interpolation durchgeführt wird. Dies ist nützlich, wenn einige der Eingabedimensionen inkommensurable Einheiten haben und sich um viele Größenordnungen unterscheiden.

Hinzugefügt in Version 0.14.0.

Rückgabe:

ndarray: Array der interpolierten Werte.

Siehe auch

LinearNDInterpolator: Stückweiser linearer Interpolator in N Dimensionen.
NearestNDInterpolator: Nearest-Neighbor-Interpolator in N Dimensionen.
CloughTocher2DInterpolator: Stückweise kubischer, C1-glatter, Krümmungsminimierender Interpolator in 2D.
interpn: Interpolation auf einem regulären Gitter oder einem rechtwinkligen Gitter.
RegularGridInterpolator: Interpolator auf einem regulären oder rechtwinkligen Gitter in beliebigen Dimensionen (interpn umschließt diese Klasse).

Hinweise

Hinzugefügt in Version 0.9.

Hinweis

Für Daten auf einem regulären Gitter verwenden Sie stattdessen interpn.

Beispiele

Angenommen, wir möchten die 2-D-Funktion interpolieren

>>> import numpy as np
>>> def func(x, y):
...     return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

auf einem Gitter in [0, 1]x[0, 1]

>>> grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]

aber wir kennen ihre Werte nur an 1000 Datenpunkten

>>> rng = np.random.default_rng()
>>> points = rng.random((1000, 2))
>>> values = func(points[:,0], points[:,1])

Dies kann mit griddata erfolgen – unten probieren wir alle Interpolationsmethoden aus

>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')

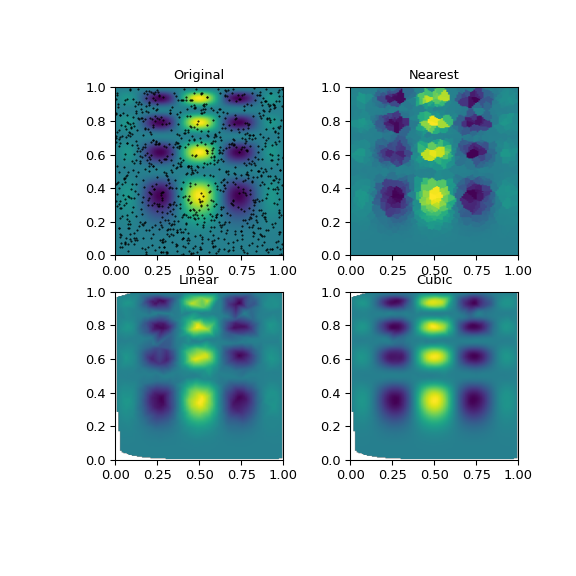
Man kann sehen, dass das exakte Ergebnis bis zu einem gewissen Grad von allen Methoden reproduziert wird, aber für diese glatte Funktion liefert das stückweise kubische Interpolationsverfahren die besten Ergebnisse

>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower')
>>> plt.plot(points[:,0], points[:,1], 'k.', ms=1)
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()

../../_images/scipy-interpolate-griddata-1.png