scipy.interpolate.

baryzentrische_interpolation#

scipy.interpolate.baryzentrische_interpolation(xi, yi, x, achse=0, *, der=0, rng=None)[Quelle]#

Bequeme Funktion für die baryzentrische Interpolation.

Konstruiert ein Polynom, das durch einen gegebenen Satz von Punkten verläuft, und wertet dann das Polynom aus. Aus Gründen der numerischen Stabilität berechnet diese Funktion nicht die Koeffizienten des Polynoms.

Diese Funktion verwendet eine „baryzentrische Interpolationsmethode“, die das Problem als Sonderfall der rationalen Funktionsinterpolation behandelt. Dieser Algorithmus ist numerisch recht stabil, aber selbst in einer Welt exakter Berechnungen ist Polynominterpolation ein sehr schlecht konditionierter Prozess, es sei denn, die x-Koordinaten werden sehr sorgfältig gewählt – Tschebyscheff-Nullstellen (z. B. cos(i*pi/n)) sind eine gute Wahl – aufgrund des Runge-Phänomens.

Parameter:

xiarray_like: 1-D-Array der x-Koordinaten der Punkte, durch die das Polynom verlaufen soll
yiarray_like: Die y-Koordinaten der Punkte, durch die das Polynom verlaufen soll.
xSkalar oder array_like: Punkt oder Punkte, an denen der Interpolator ausgewertet werden soll.
axisint, optional: Achse im yi-Array, die den x-Koordinatenwerten entspricht.
derint oder list oder None, optional: Wie viele Ableitungen ausgewertet werden sollen, oder None für alle potenziell nicht-null Ableitungen (d. h. eine Zahl gleich der Anzahl der Punkte) oder eine Liste der auszuwertenden Ableitungen. Diese Zahl enthält den Funktionswert als '0-te' Ableitung.
rngnumpy.random.Generator, optional: Zustand des Pseudozufallszahlengenerators. Wenn rng None ist, wird ein neuer numpy.random.Generator unter Verwendung von Entropie aus dem Betriebssystem erstellt. Typen außer numpy.random.Generator werden an numpy.random.default_rng übergeben, um einen Generator zu instanziieren.

Rückgabe:

ySkalar oder array_like: Interpolierte Werte. Die Form wird bestimmt, indem die Interpolationsachse im ursprünglichen Array durch die Form von x ersetzt wird.

Siehe auch

BarycentricInterpolator: Baryzentrischer Interpolator

Hinweise

Die Konstruktion der Interpolationsgewichte ist ein relativ langsamer Prozess. Wenn Sie dies viele Male mit demselben xi (aber möglicherweise unterschiedlichen yi oder x) aufrufen möchten, sollten Sie die Klasse BarycentricInterpolator verwenden. Dies ist das, was diese Funktion intern verwendet.

Beispiele

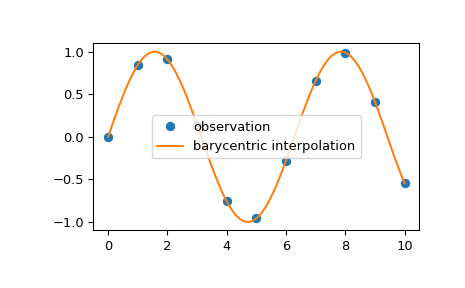
Wir können 2D beobachtete Daten mit baryzentrischer Interpolation interpolieren

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import barycentric_interpolate
>>> x_observed = np.linspace(0.0, 10.0, 11)
>>> y_observed = np.sin(x_observed)
>>> x = np.linspace(min(x_observed), max(x_observed), num=100)
>>> y = barycentric_interpolate(x_observed, y_observed, x)
>>> plt.plot(x_observed, y_observed, "o", label="observation")
>>> plt.plot(x, y, label="barycentric interpolation")
>>> plt.legend()
>>> plt.show()

../../_images/scipy-interpolate-barycentric_interpolate-1.png