scipy.interpolate.

make_smoothing_spline#

scipy.interpolate.make_smoothing_spline(x, y, w=None, lam=None, *, axis=0)[Quelle]#

Erzeugt eine glättende B-Spline, die das Kriterium der verallgemeinerten Kreuzvalidierung (GCV) erfüllt.

Berechnet die (Koeffizienten der) glättenden kubischen Spline-Funktion unter Verwendung von lam zur Steuerung des Kompromisses zwischen dem Grad der Glattheit der Kurve und ihrer Nähe zu den Daten. Wenn lam None ist, wird es anhand des GCV-Kriteriums [1] ermittelt.

Eine glättende Spline wird als Lösung des regulierten gewichteten linearen Regressionsproblems gefunden:

\[\sum\limits_{i=1}^n w_i\lvert y_i - f(x_i) \rvert^2 + \lambda\int\limits_{x_1}^{x_n} (f^{(2)}(u))^2 d u\]

wobei \(f\) eine Spline-Funktion, \(w\) ein Vektor von Gewichten und \(\lambda\) ein Regularisierungsparameter ist.

Wenn lam None ist, verwenden wir das GCV-Kriterium, um einen optimalen Regularisierungsparameter zu finden, andernfalls lösen wir das regulierte gewichtete lineare Regressionsproblem mit dem gegebenen Parameter. Der Parameter steuert den Kompromiss auf folgende Weise: Je größer der Parameter wird, desto glatter wird die Funktion.

Parameter:

xarray_like, Form (n,): Abzissen. n muss mindestens 5 sein.
yarray_like, Form (n, …): Ordinaten. n muss mindestens 5 sein.
warray_like, shape (n,), optional: Vektor der Gewichte. Standard ist np.ones_like(x).
lamfloat, (\(\lambda \geq 0\)), optional: Regularisierungsparameter. Wenn lam None ist, wird er aus dem GCV-Kriterium ermittelt. Standard ist None.
axisint, optional: Die Datenachse. Standard ist Null. Es wird angenommen, dass y.shape[axis] == n ist und alle anderen Achsen von y Batch-Achsen sind.

Rückgabe:

funcBSpline Objekt: Ein Objekt, das eine Spline in der B-Spline-Basis als Lösung des Problems der glättenden Splines mittels des GCV-Kriteriums [1] darstellt, falls lam None ist, andernfalls unter Verwendung des gegebenen Parameters lam.

Hinweise

Dieser Algorithmus ist eine Neuimplementierung des von Woltring in FORTRAN [2] eingeführten Algorithmus in Eigenregie. Die ursprüngliche Version kann aufgrund von Lizenzproblemen nicht im SciPy-Quellcode verwendet werden. Die Details der Neuimplementierung werden hier diskutiert (nur auf Russisch verfügbar) [4].

Wenn der Gewichtsvektor w None ist, nehmen wir an, dass alle Punkte gleiches Gewicht haben und der Gewichtsvektor ein Vektor von Einsen ist.

Beachten Sie, dass im gewichteten Residuenquadratsumme die Gewichte nicht quadriert werden: \(\sum\limits_{i=1}^n w_i\lvert y_i - f(x_i) \rvert^2\), während in splrep die Summe aus den quadrierten Gewichten gebildet wird.

In Fällen, in denen das ursprüngliche Problem schlecht gestellt ist (z. B. das Produkt \(X^T W X\), wobei \(X\) eine Designmatrix ist, keine positiv definierte Matrix ist), wird ein ValueError ausgelöst.

Referenzen

[1]

G. Wahba, „Estimating the smoothing parameter“ in Spline models for observational data, Philadelphia, Pennsylvania: Society for Industrial and Applied Mathematics, 1990, S. 45-65. DOI:10.1137/1.9781611970128

[2]

H. J. Woltring, A Fortran package for generalized, cross-validatory spline smoothing and differentiation, Advances in Engineering Software, Bd. 8, Nr. 2, S. 104-113, 1986. DOI:10.1016/0141-1195(86)90098-7

[3]

T. Hastie, J. Friedman und R. Tisbshirani, „Smoothing Splines“ in The elements of Statistical Learning: Data Mining, Inference, and prediction, New York: Springer, 2017, S. 241-249. DOI:10.1007/978-0-387-84858-7

[4]

E. Zemlyanoy, „Generalized cross-validation smoothing splines“, BSc-Arbeit, 2022. https://www.hse.ru/ba/am/students/diplomas/620910604 (auf Russisch)

Beispiele

Generieren einiger verrauschter Daten

>>> import numpy as np
>>> np.random.seed(1234)
>>> n = 200
>>> def func(x):
...    return x**3 + x**2 * np.sin(4 * x)
>>> x = np.sort(np.random.random_sample(n) * 4 - 2)
>>> y = func(x) + np.random.normal(scale=1.5, size=n)

Erzeugt eine glättende Spline-Funktion

>>> from scipy.interpolate import make_smoothing_spline
>>> spl = make_smoothing_spline(x, y)

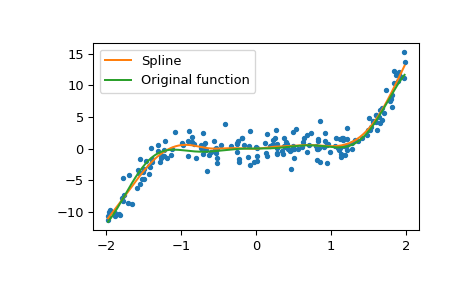
Beides plotten

>>> import matplotlib.pyplot as plt
>>> grid = np.linspace(x[0], x[-1], 400)
>>> plt.plot(x, y, '.')
>>> plt.plot(grid, spl(grid), label='Spline')
>>> plt.plot(grid, func(grid), label='Original function')
>>> plt.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-make_smoothing_spline-1.png