scipy.optimize.

bracket#

scipy.optimize.bracket(func, xa=0.0, xb=1.0, args=(), grow_limit=110.0, maxiter=1000)[Quelle]#

Klammert das Minimum einer Funktion ein.

Sucht ausgehend von einer Funktion und zwei unterschiedlichen Anfangspunkten in Richtung des Gefälles (definiert durch die Anfangspunkte) und gibt drei Punkte zurück, die das Minimum der Funktion einklammern.

Parameter:

funccallable f(x,*args): Zielfunktion zur Minimierung.
xa, xbfloat, optional: Anfangspunkte. Standardmäßig xa auf 0.0 und xb auf 1.0 gesetzt. Ein lokales Minimum muss nicht unbedingt in diesem Intervall enthalten sein.
argstuple, optional: Zusätzliche Argumente (falls vorhanden), die an func übergeben werden.
grow_limitfloat, optional: Maximale Wachstumsbegrenzung. Standardwert ist 110.0
maxiterint, optional: Maximale Anzahl von Iterationen, die durchgeführt werden sollen. Standardwert ist 1000.

Rückgabe:

xa, xb, xcfloat: Endpunkte der Klammer.
fa, fb, fcfloat: Funktionswerte am Klammerpunkt.
funcallsint: Anzahl der durchgeführten Funktionsaufrufe.

Löst aus:

BracketError: Wenn vor Beendigung des Algorithmus keine gültige Klammer gefunden wird. Siehe Hinweise für Bedingungen einer gültigen Klammer.

Hinweise

Der Algorithmus versucht, drei streng geordnete Punkte zu finden (d.h. \(x_a < x_b < x_c\) oder \(x_c < x_b < x_a\)), die \(f(x_b) ≤ f(x_a)\) und \(f(x_b) ≤ f(x_c)\) erfüllen, wobei eine der Ungleichungen streng erfüllt sein muss und alle \(x_i\) endlich sein müssen.

Beispiele

Diese Funktion kann eine abwärts konvexe Region einer Funktion finden

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.optimize import bracket
>>> def f(x):
...     return 10*x**2 + 3*x + 5
>>> x = np.linspace(-2, 2)
>>> y = f(x)
>>> init_xa, init_xb = 0.1, 1
>>> xa, xb, xc, fa, fb, fc, funcalls = bracket(f, xa=init_xa, xb=init_xb)
>>> plt.axvline(x=init_xa, color="k", linestyle="--")
>>> plt.axvline(x=init_xb, color="k", linestyle="--")
>>> plt.plot(x, y, "-k")
>>> plt.plot(xa, fa, "bx")
>>> plt.plot(xb, fb, "rx")
>>> plt.plot(xc, fc, "bx")
>>> plt.show()

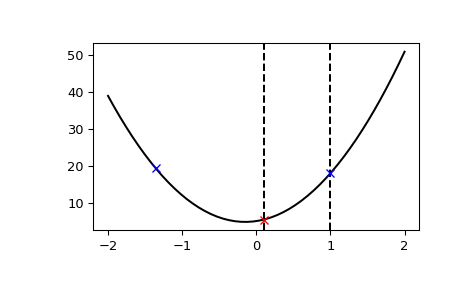
../../_images/scipy-optimize-bracket-1_00_00.png

Beachten Sie, dass beide Anfangspunkte rechts vom Minimum lagen und der dritte Punkt in Richtung des "Gefälles" gefunden wurde – der Richtung, in der die Funktion abnahm (nach links). Die Endpunkte sind streng geordnet, und der Funktionswert am mittleren Punkt ist kleiner als die Funktionswerte an den Endpunkten; daraus folgt, dass ein Minimum innerhalb der Klammer liegen muss.