curve_fit#
- scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=None, bounds=(-inf, inf), method=None, jac=None, *, full_output=False, nan_policy=None, **kwargs)[Quelle]#
Verwendet nichtlineare kleinste Quadrate, um eine Funktion f an Daten anzupassen.
Nimmt an, dass
ydata = f(xdata, *params) + eps.- Parameter:
- faufrufbar
Die Modellfunktion, f(x, …). Sie muss die unabhängige Variable als erstes Argument und die anzupassenden Parameter als separate verbleibende Argumente enthalten.
- xdataarray_like
Die unabhängige Variable, an der die Daten gemessen werden. Sollte normalerweise eine Sequenz der Länge M sein oder ein Array der Form (k,M) für Funktionen mit k Prädiktoren, und jedes Element sollte float-konvertierbar sein, wenn es sich um ein Array-ähnliches Objekt handelt.
- ydataarray_like
Die abhängigen Daten, ein Array der Länge M – nominell
f(xdata, ...).- p0array_like, optional
Anfangsschätzung für die Parameter (Länge N). Wenn None, dann sind die Anfangswerte alle 1 (wenn die Anzahl der Parameter für die Funktion durch Introspektion bestimmt werden kann, andernfalls wird ein ValueError ausgelöst).
- sigmaNone oder Skalar oder Sequenz der Länge M oder MxM-Array, optional
Bestimmt die Unsicherheit in ydata. Wenn wir Residuen als
r = ydata - f(xdata, *popt)definieren, dann hängt die Interpretation von sigma von seiner Dimensionalität abEin Skalar oder 1D sigma sollte Werte der Standardabweichungen von Fehlern in ydata enthalten. In diesem Fall ist die optimierte Funktion
chisq = sum((r / sigma) ** 2).Ein 2D sigma sollte die Kovarianzmatrix der Fehler in ydata enthalten. In diesem Fall ist die optimierte Funktion
chisq = r.T @ inv(sigma) @ r.Hinzugefügt in Version 0.19.
None (Standard) ist äquivalent zu 1D sigma, gefüllt mit Einsen.
- absolute_sigmabool, optional
Wenn True, wird sigma absolut verwendet und die geschätzte Parameterkovarianz pcov spiegelt diese absoluten Werte wider.
Wenn False (Standard), sind nur die relativen Größen der sigma-Werte relevant. Die zurückgegebene Parameterkovarianzmatrix pcov basiert auf der Skalierung von sigma um einen konstanten Faktor. Diese Konstante wird so bestimmt, dass die reduzierte chisq für die optimalen Parameter popt bei Verwendung des *skalierten* sigma gleich eins ist. Anders ausgedrückt, sigma wird skaliert, um die Stichprobenvarianz der Residuen nach der Anpassung anzupassen. Standard ist False. Mathematisch gilt
pcov(absolute_sigma=False) = pcov(absolute_sigma=True) * chisq(popt)/(M-N)- check_finitebool, optional
Wenn True, wird überprüft, ob die Eingabearrays keine NaNs oder Inf-Werte enthalten, und ein ValueError ausgelöst, falls dies der Fall ist. Das Setzen dieses Parameters auf False kann stillschweigend unsinnige Ergebnisse liefern, wenn die Eingabearrays NaNs enthalten. Standard ist True, wenn nan_policy nicht explizit angegeben ist, und andernfalls False.
- bounds2-Tupel aus array_like oder
Bounds, optional Untere und obere Schranken für die Parameter. Standard ist keine Schranken. Es gibt zwei Möglichkeiten, die Schranken anzugeben
Instanz der Klasse
Bounds.2-Tupel aus array_like: Jedes Element des Tupels muss entweder ein Array mit der Länge gleich der Anzahl der Parameter sein oder ein Skalar (in diesem Fall wird die Schranke für alle Parameter gleich angenommen). Verwenden Sie
np.infmit dem entsprechenden Vorzeichen, um Schranken für alle oder einige Parameter zu deaktivieren.
- method{‘lm’, ‘trf’, ‘dogbox’}, optional
Zu verwendende Methode für die Optimierung. Weitere Details finden Sie unter
least_squares. Standard ist ‘lm’ für unbeschränkte Probleme und ‘trf’, wenn bounds angegeben sind. Die Methode ‘lm’ funktioniert nicht, wenn die Anzahl der Beobachtungen kleiner ist als die Anzahl der Variablen, verwenden Sie in diesem Fall ‘trf’ oder ‘dogbox’.Hinzugefügt in Version 0.17.
- jaccallable, string oder None, optional
Funktion mit der Signatur
jac(x, ...), die die Jacobi-Matrix der Modellfunktion in Bezug auf die Parameter als dichtes Array-ähnliches Gebilde berechnet. Sie wird gemäß dem bereitgestellten sigma skaliert. Wenn None (Standard), wird die Jacobi-Matrix numerisch geschätzt. String-Schlüsselwörter für die Methoden ‘trf’ und ‘dogbox’ können verwendet werden, um ein Schema für endliche Differenzen auszuwählen, sieheleast_squares.Hinzugefügt in Version 0.18.
- full_outputboolean, optional
Wenn True, gibt diese Funktion zusätzliche Informationen zurück: infodict, mesg und ier.
Hinzugefügt in Version 1.9.
- nan_policy{‘raise’, ‘omit’, None}, optional
Definiert, wie mit NaNs in den Eingaben umgegangen wird. Die folgenden Optionen sind verfügbar (Standard ist None)
‘raise’: löst einen Fehler aus
‘omit’: führt die Berechnungen unter Ignorierung von NaN-Werten durch
None: es wird keine spezielle Behandlung von NaNs durchgeführt (außer dem, was von check_finite getan wird); das Verhalten bei Vorhandensein von NaNs ist implementierungsabhängig und kann sich ändern.
Beachten Sie, dass, wenn dieser Wert explizit angegeben wird (nicht None), check_finite auf False gesetzt wird.
Hinzugefügt in Version 1.11.
- **kwargs
Schlüsselwortargumente, die an
leastsqfürmethod='lm'oder ansonsten anleast_squaresübergeben werden.
- Rückgabe:
- poptarray
Optimale Werte für die Parameter, so dass die Summe der quadrierten Residuen von
f(xdata, *popt) - ydataminimiert wird.- pcov2-D-Array
Die geschätzte approximative Kovarianz von popt. Die Diagonalen geben die Varianz der Parameterschätzung an. Um Fehler mit einer Standardabweichung auf die Parameter zu berechnen, verwenden Sie
perr = np.sqrt(np.diag(pcov)). Beachten Sie, dass die Beziehung zwischen cov und den Schätzungen der Parameterunsicherheit auf einer linearen Annäherung der Modellfunktion um das Optimum basiert [1]. Wenn diese Annäherung ungenau wird, liefert cov möglicherweise keine genaue Unsicherheitsmessung.Wie der sigma-Parameter die geschätzte Kovarianz beeinflusst, hängt vom Argument absolute_sigma ab, wie oben beschrieben.
Wenn die Jacobi-Matrix am Lösungsort keinen vollen Rang hat, gibt die Methode ‘lm’ eine Matrix zurück, die mit
np.infgefüllt ist. Andererseits verwenden die Methoden ‘trf’ und ‘dogbox’ die Moore-Penrose-Pseudoinverse, um die Kovarianzmatrix zu berechnen. Kovarianzmatrizen mit großen Konditionszahlen (z.B. berechnet mitnumpy.linalg.cond) können darauf hindeuten, dass die Ergebnisse unzuverlässig sind.- infodictdict (nur zurückgegeben, wenn full_output True ist)
ein Dictionary optionaler Ausgaben mit den Schlüsseln
nfevDie Anzahl der Funktionsaufrufe. Die Methoden ‘trf’ und ‘dogbox’ zählen keine Funktionsaufrufe für die numerische Jacobi-Approximation, im Gegensatz zur Methode ‘lm’.
fvecDie Residuenwerte, die an der Lösung ausgewertet wurden; für ein 1D- sigma ist dies
(f(x, *popt) - ydata)/sigma.fjacEine Permutation der R-Matrix einer QR-Zerlegung der endgültigen approximierten Jacobi-Matrix, spaltenweise gespeichert. Zusammen mit ipvt kann die Kovarianz der Schätzung approximiert werden. Methode ‘lm’ liefert nur diese Informationen.
ipvtEin Integer-Array der Länge N, das eine Permutationsmatrix p definiert, so dass fjac*p = q*r, wobei r obere Dreiecksmatrix mit Diagonalelementen abnehmender Größe ist. Spalte j von p ist Spalte ipvt(j) der Identitätsmatrix. Methode ‘lm’ liefert nur diese Informationen.
qtfDer Vektor (transpose(q) * fvec). Methode ‘lm’ liefert nur diese Informationen.
Hinzugefügt in Version 1.9.
- mesgstr (nur zurückgegeben, wenn full_output True ist)
Eine Meldung, die Informationen über die Lösung liefert.
Hinzugefügt in Version 1.9.
- ierint (nur zurückgegeben, wenn full_output True ist)
Ein Integer-Flag. Wenn es gleich 1, 2, 3 oder 4 ist, wurde die Lösung gefunden. Andernfalls wurde die Lösung nicht gefunden. In beiden Fällen liefert die optionale Ausgabevariable mesg weitere Informationen.
Hinzugefügt in Version 1.9.
- Löst aus:
- ValueError
wenn entweder ydata oder xdata NaNs enthalten oder wenn inkompatible Optionen verwendet werden.
- RuntimeError
wenn die Minimierung der kleinsten Quadrate fehlschlägt.
- OptimizeWarning
wenn die Kovarianz der Parameter nicht geschätzt werden kann.
Siehe auch
least_squaresMinimiert die Summe der Quadrate nichtlinearer Funktionen.
scipy.stats.linregressBerechnet eine lineare Regression nach der Methode der kleinsten Quadrate für zwei Datensätze.
Hinweise
Benutzer sollten sicherstellen, dass die Eingaben xdata, ydata und die Ausgabe von f vom Typ
float64sind, da sonst die Optimierung falsche Ergebnisse liefern kann.Mit
method='lm'verwendet der Algorithmus den Levenberg-Marquardt-Algorithmus überleastsq. Beachten Sie, dass dieser Algorithmus nur unbeschränkte Probleme behandeln kann.Box-Beschränkungen können mit den Methoden ‘trf’ und ‘dogbox’ behandelt werden. Weitere Informationen finden Sie im Docstring von
least_squares.Parameter, die angepasst werden sollen, müssen eine ähnliche Skalierung aufweisen. Unterschiede von mehreren Größenordnungen können zu falschen Ergebnissen führen. Für die Methoden ‘trf’ und ‘dogbox’ kann das Schlüsselwortargument x_scale zur Skalierung der Parameter verwendet werden.
curve_fitdient der lokalen Optimierung von Parametern zur Minimierung der Summe der quadrierten Residuen. Für globale Optimierung, andere Wahlmöglichkeiten der Zielfunktion und andere fortgeschrittene Funktionen sollten Sie die Globalen Optimierungswerkzeuge von SciPy oder das Paket LMFIT in Betracht ziehen.Referenzen
[1]K. Vugrin et al. Confidence region estimation techniques for nonlinear regression in groundwater flow: Three case studies. Water Resources Research, Vol. 43, W03423, DOI:10.1029/2005WR004804
Beispiele
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.optimize import curve_fit
>>> def func(x, a, b, c): ... return a * np.exp(-b * x) + c
Definieren Sie die Daten, die mit etwas Rauschen angepasst werden sollen
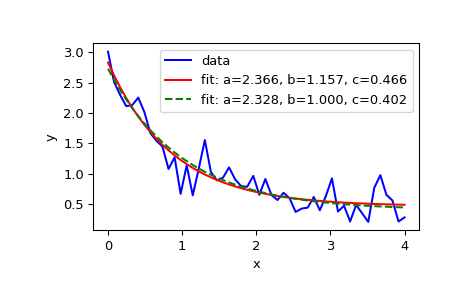
>>> xdata = np.linspace(0, 4, 50) >>> y = func(xdata, 2.5, 1.3, 0.5) >>> rng = np.random.default_rng() >>> y_noise = 0.2 * rng.normal(size=xdata.size) >>> ydata = y + y_noise >>> plt.plot(xdata, ydata, 'b-', label='data')
Passen Sie die Parameter a, b, c der Funktion func an
>>> popt, pcov = curve_fit(func, xdata, ydata) >>> popt array([2.56274217, 1.37268521, 0.47427475]) >>> plt.plot(xdata, func(xdata, *popt), 'r-', ... label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
Beschränken Sie die Optimierung auf den Bereich von
0 <= a <= 3,0 <= b <= 1und0 <= c <= 0.5>>> popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5])) >>> popt array([2.43736712, 1. , 0.34463856]) >>> plt.plot(xdata, func(xdata, *popt), 'g--', ... label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
>>> plt.xlabel('x') >>> plt.ylabel('y') >>> plt.legend() >>> plt.show()
Für zuverlässige Ergebnisse sollte das Modell func nicht überparametrisiert sein; redundante Parameter können zu unzuverlässigen Kovarianzmatrizen und in einigen Fällen zu schlechteren Anpassungsergebnissen führen. Als schnelle Überprüfung, ob das Modell überparametrisiert sein könnte, berechnen Sie die Konditionszahl der Kovarianzmatrix
>>> np.linalg.cond(pcov) 34.571092161547405 # may vary
Der Wert ist klein, daher gibt er wenig Anlass zur Sorge. Wenn wir jedoch einen vierten Parameter
dzu func hinzufügen würden, mit der gleichen Auswirkung wiea>>> def func2(x, a, b, c, d): ... return a * d * np.exp(-b * x) + c # a and d are redundant >>> popt, pcov = curve_fit(func2, xdata, ydata) >>> np.linalg.cond(pcov) 1.13250718925596e+32 # may vary
Ein solch großer Wert ist Anlass zur Sorge. Die Diagonalelemente der Kovarianzmatrix, die mit der Unsicherheit der Anpassung zusammenhängen, geben mehr Aufschluss
>>> np.diag(pcov) array([1.48814742e+29, 3.78596560e-02, 5.39253738e-03, 2.76417220e+28]) # may vary
Beachten Sie, dass das erste und letzte Glied viel größer sind als die anderen Elemente, was darauf hindeutet, dass die optimalen Werte dieser Parameter mehrdeutig sind und dass nur einer dieser Parameter im Modell benötigt wird.
Wenn die optimalen Parameter von f um mehrere Größenordnungen voneinander abweichen, kann die resultierende Anpassung ungenau sein. Manchmal schlägt
curve_fitfehl, keine Ergebnisse zu finden>>> ydata = func(xdata, 500000, 0.01, 15) >>> try: ... popt, pcov = curve_fit(func, xdata, ydata, method = 'trf') ... except RuntimeError as e: ... print(e) Optimal parameters not found: The maximum number of function evaluations is exceeded.
Wenn die Parameterskalierung im Voraus ungefähr bekannt ist, kann sie im Argument x_scale angegeben werden
>>> popt, pcov = curve_fit(func, xdata, ydata, method = 'trf', ... x_scale = [1000, 1, 1]) >>> popt array([5.00000000e+05, 1.00000000e-02, 1.49999999e+01])