scipy.signal.ShortTimeFFT.

spectrogram

ShortTimeFFT.spectrogram(x, y=None, detr=None, *, p0=None, p1=None, k_offset=0, padding='zeros', axis=-1)

Berechnet Spektrogramm oder Kreuzspektrogramm.

Das Spektrogramm ist das absolute Quadrat der STFT, d. h. es ist abs(S[q,p])**2 für gegebene S[q,p] und somit immer nicht-negativ. Für zwei STFTs Sx[q,p], Sy[q,p] ist das Kreuzspektrogramm definiert als Sx[q,p] * np.conj(Sy[q,p]) und ist komplexwertig. Dies ist eine Hilfsfunktion zum Aufrufen von stft / stft_detrend, daher werden alle Parameter dort besprochen.

Parameter:

xnp.ndarray

Das Eingabesignal als reell- oder komplexwertiges Array. Bei komplexen Werten muss die Eigenschaft fft_mode auf ‘twosided’ oder ‘centered’ gesetzt sein.

ynp.ndarray

Das zweite Eingangssignal mit derselben Form wie x. Wenn None, wird angenommen, dass es x ist. Bei komplexen Werten muss die Eigenschaft fft_mode auf ‘twosided’ oder ‘centered’ gesetzt sein.

detr‘linear’ | ‘constant’ | Callable[[np.ndarray], np.ndarray] | None

Wenn ‘constant’, wird der Mittelwert subtrahiert, wenn auf "linear" gesetzt, wird der lineare Trend aus jedem Segment entfernt. Dies geschieht durch Aufrufen von detrend. Wenn detr eine Funktion mit einem Parameter ist, wird detr auf jedes Segment angewendet. Für None (Standard) werden keine Trends entfernt.

p0int | None

Das erste Element des Bereichs von Slices, für die berechnet werden soll. Wenn None, wird es auf p_min gesetzt, was der kleinstmögliche Slice ist.

p1int | None

Das Ende des Arrays. Wenn None, wird p_max(n) verwendet.

k_offsetint

Index des ersten Samples (t = 0) in x.

padding‘zeros’ | ‘edge’ | ‘even’ | ‘odd’

Art der hinzugefügten Werte, wenn das gleitende Fenster an einem oder beiden Enden des Eingangs x übersteht. Nullen werden hinzugefügt, wenn der Standardwert 'zeros' gesetzt ist. Für 'edge' wird entweder der erste oder der letzte Wert von x verwendet. 'even' polstert durch Spiegelung des Signals am ersten oder letzten Sample und 'odd' multipliziert es zusätzlich mit -1.

axisint

Die Achse von x, über die die STFT berechnet werden soll. Wenn nicht angegeben, wird die letzte Achse verwendet.

Rückgabe:

S_xynp.ndarray

Ein reellwertiges Array mit nicht-negativen Werten wird zurückgegeben, wenn x ist y oder y ist None. Die Dimension ist immer um eins größer als die von x. Die letzte Achse repräsentiert immer die Zeitscheiben des Spektrogramms. axis definiert die Frequenzachse (standardmäßig die vorletzte). Zum Beispiel, für ein eindimensionales x wird ein komplexes 2D-Array zurückgegeben, wobei Achse 0 die Frequenz und Achse 1 die Zeitscheiben darstellt.

Siehe auch

stft

Führt die Kurzzeittransformation durch.

stft_detrend

STFT mit einem von jedem Segment subtrahierten Trend.

scipy.signal.ShortTimeFFT

Klasse, zu der diese Methode gehört.

Hinweise

Das Kreuzspektrogramm kann als das Zeit-Frequenz-Analogon der Kreuzspektraldichte interpretiert werden (siehe csd). Das absolute Quadrat |Sxy|² eines Kreuzspektrogramms Sxy, geteilt durch die Spektrogramme Sxx und Syy, kann als Kohärenzspektrogramm Cxy := abs(Sxy)**2 / (Sxx*Syy) interpretiert werden, was das Zeit-Frequenz-Analogon zu coherence ist.

Wenn die STFT so parametrisiert ist, dass sie eine unitäre Transformation darstellt, d. h. durch Verwendung von from_win_equals_dual, dann wird der Wert des Skalarprodukts und somit auch die Energie erhalten.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Das folgende Beispiel zeigt das Spektrogramm einer Rechteckwelle mit variierender Frequenz \(f_i(t)\) (markiert durch eine grüne gestrichelte Linie im Diagramm), abgetastet mit 20 Hz. Das verwendete Gaußsche Fenster ist 50 Samples oder 2,5 s lang. Für die ShortTimeFFT wurde der Parameter mfft=800 (Überabtastfaktor 16) und ein hop-Intervall von 2 gewählt, um eine ausreichende Anzahl von Punkten zu erzeugen.

Die Kolorierung des Diagramms ist logarithmisch skaliert, da die Leistungsspektraldichte in dB angegeben ist. Die zeitliche Ausdehnung des Signals x ist durch vertikale gestrichelte Linien markiert, und die schattierten Bereiche kennzeichnen das Vorhandensein von Randeffekten.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import square, ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T_x, N = 1 / 20, 1000  # 20 Hz sampling rate for 50 s signal
>>> t_x = np.arange(N) * T_x  # time indexes for signal
>>> f_i = 5e-3*(t_x - t_x[N // 3])**2 + 1  # varying frequency
>>> x = square(2*np.pi*np.cumsum(f_i)*T_x)  # the signal
...
>>> g_std = 12  # standard deviation for Gaussian window in samples
>>> win = gaussian(50, std=g_std, sym=True)  # symmetric Gaussian wind.
>>> SFT = ShortTimeFFT(win, hop=2, fs=1/T_x, mfft=800, scale_to='psd')
>>> Sx2 = SFT.spectrogram(x)  # calculate absolute square of STFT
...
>>> fig1, ax1 = plt.subplots(figsize=(6., 4.))  # enlarge plot a bit
>>> t_lo, t_hi = SFT.extent(N)[:2]  # time range of plot
>>> ax1.set_title(rf"Spectrogram ({SFT.m_num*SFT.T:g}$\,s$ Gaussian " +
...               rf"window, $\sigma_t={g_std*SFT.T:g}\,$s)")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, " +
...                rf"$\Delta t = {SFT.delta_t:g}\,$s)",
...         ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, " +
...                rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",
...         xlim=(t_lo, t_hi))
>>> Sx_dB = 10 * np.log10(np.fmax(Sx2, 1e-4))  # limit range to -40 dB
>>> im1 = ax1.imshow(Sx_dB, origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='magma')
>>> ax1.plot(t_x, f_i, 'g--', alpha=.5, label='$f_i(t)$')
>>> fig1.colorbar(im1, label='Power Spectral Density ' +
...                          r"$20\,\log_{10}|S_x(t, f)|$ in dB")
...
>>> # Shade areas where window slices stick out to the side:
>>> for t0_, t1_ in [(t_lo, SFT.lower_border_end[0] * SFT.T),
...                  (SFT.upper_border_begin(N)[0] * SFT.T, t_hi)]:
...     ax1.axvspan(t0_, t1_, color='w', linewidth=0, alpha=.3)
>>> for t_ in [0, N * SFT.T]:  # mark signal borders with vertical line
...     ax1.axvline(t_, color='c', linestyle='--', alpha=0.5)
>>> ax1.legend()
>>> fig1.tight_layout()
>>> plt.show()

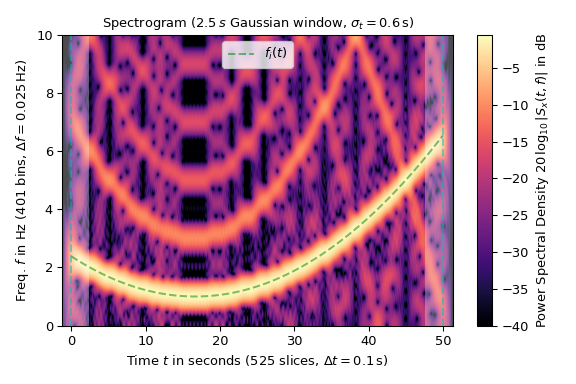
Die logarithmische Skalierung enthüllt die ungeraden Harmonischen der Rechteckwelle, die an der Nyquist-Frequenz von 10 Hz reflektiert werden. Diese Aliasing ist auch die Hauptursache für die Rauschartefakte im Diagramm.

ZurückIn Tab öffnen