scipy.signal.

ShortTimeFFT#

class scipy.signal.ShortTimeFFT(win, hop, fs, *, fft_mode='onesided', mfft=None, dual_win=None, scale_to=None, phase_shift=0)[Quelle]#

Bietet eine parametrisierte diskrete Kurzzeit-Fourier-Transformation (stft) und ihre Inverse (istft).

Die stft berechnet sequentielle FFTs, indem ein Fenster (win) mit hop-Inkrementen über ein Eingangssignal gleitet. Sie kann verwendet werden, um die Änderung des Spektrums über die Zeit zu quantifizieren.

Die stft wird durch eine komplexwertige Matrix S[q,p] dargestellt, wobei die p-te Spalte eine FFT mit dem um die Zeit t[p] = p * delta_t = p * hop * T zentrierte FFT repräsentiert, wobei T das Abtastintervall des Eingangssignals ist. Die q-te Zeile repräsentiert die Werte bei der Frequenz f[q] = q * delta_f, wobei delta_f = 1 / (mfft * T) die Bündelbreite der FFT ist.

Die inverse STFT istft wird durch Umkehrung der Schritte der STFT berechnet: Nimm die IFFT des p-ten Slices von S[q,p] und multipliziere das Ergebnis mit dem sogenannten dualen Fenster (siehe dual_win). Verschiebe das Ergebnis um p * delta_t und addiere das Ergebnis zu den vorherigen verschobenen Ergebnissen, um das Signal zu rekonstruieren. Wenn nur das duale Fenster bekannt ist und die STFT invertierbar ist, kann from_dual verwendet werden, um diese Klasse zu instanziieren.

Standardmäßig wird das sogenannte kanonische duale Fenster verwendet. Dies ist das Fenster mit der minimalen Energie unter allen möglichen dualen Fenstern. from_win_equals_dual und closest_STFT_dual_window bieten Möglichkeiten, alternative duale Fenster zu nutzen. Beachten Sie, dass win immer auch ein duales Fenster von dual_win ist.

Aufgrund der Konvention, dass die Zeit t = 0 am ersten Sample des Eingangssignals liegt, haben die STFT-Werte typischerweise negative Zeitschlitze. Daher bedeuten negative Indizes wie p_min oder k_min nicht das Zurückzählen vom Ende eines Arrays wie bei der Standard-Python-Indizierung, sondern das Links-Sein von t = 0.

Detailliertere Informationen finden Sie im Abschnitt Short-Time Fourier Transform im SciPy User Guide.

Beachten Sie, dass alle Parameter des Initialisierers, mit Ausnahme von scale_to (das scaling verwendet), identisch benannte Attribute haben.

Parameter:

winnp.ndarray: Das Fenster muss ein reelles oder komplexes 1D-Array sein.
hopint: Der Schritt in Samples, um den das Fenster bei jedem Schritt verschoben wird.
fsfloat: Abtastfrequenz des Eingangssignals und des Fensters. Ihre Beziehung zum Abtastintervall T ist T = 1 / fs.
fft_mode‘twosided’, ‘centered’, ‘onesided’, ‘onesided2X’: Modus der zu verwendenden FFT (Standard 'onesided'). Siehe Eigenschaft fft_mode für Details.
mfft: int | None: Länge der FFT, wenn eine Null-Padding-FFT gewünscht wird. Wenn None (Standard), wird die Länge des Fensters win verwendet.
dual_winnp.ndarray | None: Das duale Fenster von win. Wenn auf None gesetzt, wird es bei Bedarf berechnet.
scale_to‘magnitude’, ‘psd’ | None: Wenn nicht None (Standard) wird die Fensterfunktion skaliert, sodass jede STFT-Spalte entweder ein 'magnitude'-Spektrum oder ein Leistungsspektraldichtespektrum ('psd') darstellt. Dieser Parameter setzt die Eigenschaft scaling auf denselben Wert. Siehe die Methode scale_to für Details.
phase_shiftint | None: Wenn gesetzt, fügt es eine lineare Phase phase_shift / mfft * f zu jeder Frequenz f hinzu. Der Standardwert von 0 stellt sicher, dass keine Phasenverschiebung auf dem Null-Slice (in dem t=0 zentriert ist) angewendet wird. Siehe die Eigenschaft phase_shift für weitere Details.

Attribute:

T: Abtastintervall des Eingangssignals und des Fensters.
delta_f: Breite der Frequenzbins der STFT.
delta_t: Zeitinkrement der STFT.
dual_win: Duales Fenster (standardmäßig kanonisches duales Fenster).
f: Frequenzwerte der STFT.
f_pts: Anzahl der Punkte entlang der Frequenzachse.
fac_magnitude: Faktor, mit dem die STFT-Werte multipliziert werden, um jedes Frequenz-Slice auf ein Magnitudenspektrum zu skalieren.
fac_psd: Faktor, mit dem die STFT-Werte multipliziert werden, um jedes Frequenz-Slice auf eine Leistungsspektraldichte (PSD) zu skalieren.
fft_mode: Modus der verwendeten FFT ('twosided', 'centered', 'onesided' oder 'onesided2X').
fs: Abtastfrequenz des Eingangssignals und des Fensters.
hop: Zeitinkrement in Signalabtastwerten für das gleitende Fenster.
invertierbar: Prüft, ob die STFT invertierbar ist.
k_min: Der kleinstmögliche Signalindex der STFT.
unterer_rand_ende: Erster Signalindex und erster Slice-Index, die von der Vor-Pufferung unberührt bleiben.
m_num: Anzahl der Abtastwerte im Fenster win.
m_num_mid: Zentraler Index des Fensters win.
mfft: Länge der Eingabe für die verwendete FFT – kann größer sein als die Fensterlänge m_num.
onesided_fft: Gibt True zurück, wenn eine einseitige FFT verwendet wird.
p_min: Der kleinstmögliche Slice-Index.
phase_shift: Wenn gesetzt, fügt es eine lineare Phase phase_shift / mfft * f zu jedem FFT-Slice der Frequenz f hinzu.
scaling: Normalisierung, die auf die Fensterfunktion angewendet wird ('magnitude', 'psd', 'unitary' oder None).
win: Fensterfunktion als reell- oder komplexwertiges 1D-Array.

Methoden

`extent`(n[, axes_seq, center_bins])	Gibt die minimalen und maximalen Zeit-Frequenz-Werte zurück.
`from_dual`(dual_win, hop, fs, *[, fft_mode, ...])	Instanziiert eine ShortTimeFFT, indem nur ein duales Fenster bereitgestellt wird.
`from_win_equals_dual`(desired_win, hop, fs, *)	Erstellt eine Instanz, bei der das Fenster und sein Dual bis auf einen Skalierungsfaktor gleich sind.
`from_window`(win_param, fs, nperseg, noverlap, *)	Instanziiert ShortTimeFFT mithilfe von get_window.
`istft`(S[, k0, k1, f_axis, t_axis])	Inverse Kurzzeit-Fourier-Transformation.
`k_max`(n)	Erster Sample-Index nach dem Signalende, der nicht von einem Zeitslice berührt wird.
`nearest_k_p`(k[, left])	Gibt den nächsten Sample-Index k_p zurück, für den t[k_p] == t[p] gilt.
`p_max`(n)	Index des ersten nicht überlappenden oberen Zeit-Slices für eine n-Sample-Eingabe.
`p_num`(n)	Anzahl der Zeit-Slices für ein Eingangssignal mit n Samples.
`p_range`(n[, p0, p1])	Berechnet und validiert den Bereich der Slice-Indizes.
`scale_to`(scaling)	Skaliert das Fenster, um 'magnitude'- oder 'psd'-Skalierung für die STFT zu erhalten.
`spectrogram`(x[, y, detr, p0, p1, k_offset, ...])	Berechnet das Spektrogramm oder Kreuzspektrogramm.
`stft`(x[, p0, p1, k_offset, padding, axis])	Führt die Kurzzeittransformation durch.
`stft_detrend`(x, detr[, p0, p1, k_offset, ...])	Berechnet die Kurzzeit-Fourier-Transformation, wobei zuvor ein Trend von jedem Segment subtrahiert wird.
`t`(n[, p0, p1, k_offset])	Zeiten der STFT für ein Eingangssignal mit n Samples.
`upper_border_begin`(n)	Erster Signalindex und erster Slice-Index, die von der Nach-Pufferung betroffen sind.

Hinweise

Eine typische STFT-Anwendung ist die Erstellung verschiedener Arten von Zeit-Frequenz-Plots, die oft unter dem Begriff „Spektrogramm“ zusammengefasst werden. Beachten Sie, dass dieser Begriff auch verwendet wird, um explizit das absolute Quadrat einer STFT zu bezeichnen [11], wie in spectrogram.

Die STFT kann auch zum Filtern und für Filterbänke verwendet werden, wie in [12] erläutert.

Referenzen

[11]

Karlheinz Gröchenig: „Foundations of Time-Frequency Analysis“, Birkhäuser Boston 2001, 10.1007/978-1-4612-0003-1

[12]

Julius O. Smith III, „Spectral Audio Signal Processing“, Online-Buch, 2011, https://www.dsprelated.com/freebooks/sasp/

Beispiele

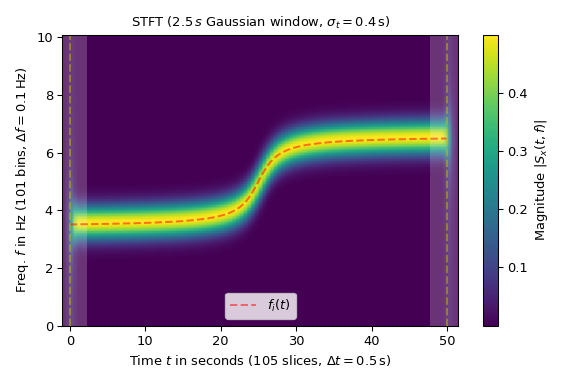
Das folgende Beispiel zeigt die Magnitude der STFT eines Sinus mit variabler Frequenz \(f_i(t)\) (im Diagramm durch eine rote gestrichelte Linie markiert)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T_x, N = 1 / 20, 1000  # 20 Hz sampling rate for 50 s signal
>>> t_x = np.arange(N) * T_x  # time indexes for signal
>>> f_i = 1 * np.arctan((t_x - t_x[N // 2]) / 2) + 5  # varying frequency
>>> x = np.sin(2*np.pi*np.cumsum(f_i)*T_x) # the signal

Das verwendete Gaußsche Fenster ist 50 Samples oder 2,5 s lang. Der Parameter mfft=200 in ShortTimeFFT bewirkt eine Übersampling des Spektrums um einen Faktor von 4.

>>> g_std = 8  # standard deviation for Gaussian window in samples
>>> w = gaussian(50, std=g_std, sym=True)  # symmetric Gaussian window
>>> SFT = ShortTimeFFT(w, hop=10, fs=1/T_x, mfft=200, scale_to='magnitude')
>>> Sx = SFT.stft(x)  # perform the STFT

Im Diagramm ist die zeitliche Ausdehnung des Signals x durch vertikale gestrichelte Linien markiert. Beachten Sie, dass die SFT Werte außerhalb des Zeitbereichs von x erzeugt. Die schattierten Bereiche links und rechts deuten auf Randeffekte hin, die durch die Fenster-Slices in diesem Bereich verursacht werden, die nicht vollständig innerhalb des Zeitbereichs von x liegen.

>>> fig1, ax1 = plt.subplots(figsize=(6., 4.))  # enlarge plot a bit
>>> t_lo, t_hi = SFT.extent(N)[:2]  # time range of plot
>>> ax1.set_title(rf"STFT ({SFT.m_num*SFT.T:g}$\,s$ Gaussian window, " +
...               rf"$\sigma_t={g_std*SFT.T}\,$s)")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, " +
...                rf"$\Delta t = {SFT.delta_t:g}\,$s)",
...         ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, " +
...                rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",
...         xlim=(t_lo, t_hi))
...
>>> im1 = ax1.imshow(abs(Sx), origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='viridis')
>>> ax1.plot(t_x, f_i, 'r--', alpha=.5, label='$f_i(t)$')
>>> fig1.colorbar(im1, label="Magnitude $|S_x(t, f)|$")
...
>>> # Shade areas where window slices stick out to the side:
>>> for t0_, t1_ in [(t_lo, SFT.lower_border_end[0] * SFT.T),
...                  (SFT.upper_border_begin(N)[0] * SFT.T, t_hi)]:
...     ax1.axvspan(t0_, t1_, color='w', linewidth=0, alpha=.2)
>>> for t_ in [0, N * SFT.T]:  # mark signal borders with vertical line:
...     ax1.axvline(t_, color='y', linestyle='--', alpha=0.5)
>>> ax1.legend()
>>> fig1.tight_layout()
>>> plt.show()

../../_images/scipy-signal-ShortTimeFFT-1_00_00.png

Die Rekonstruktion des Signals mit der istft ist unkompliziert, beachten Sie jedoch, dass die Länge von x1 angegeben werden muss, da die STFT-Länge in hop-Schritten zunimmt.

>>> SFT.invertible  # check if invertible
True
>>> x1 = SFT.istft(Sx, k1=N)
>>> np.allclose(x, x1)
True

Es ist möglich, die STFT von Signalteilen zu berechnen

>>> N2 = SFT.nearest_k_p(N // 2)
>>> Sx0 = SFT.stft(x[:N2])
>>> Sx1 = SFT.stft(x[N2:])

Beim Zusammenfügen sequentieller STFT-Teile muss die Überlappung berücksichtigt werden

>>> p0_ub = SFT.upper_border_begin(N2)[1] - SFT.p_min
>>> p1_le = SFT.lower_border_end[1] - SFT.p_min
>>> Sx01 = np.hstack((Sx0[:, :p0_ub],
...                   Sx0[:, p0_ub:] + Sx1[:, :p1_le],
...                   Sx1[:, p1_le:]))
>>> np.allclose(Sx01, Sx)  # Compare with SFT of complete signal
True

Es ist auch möglich, die itsft für Signalteile zu berechnen

>>> y_p = SFT.istft(Sx, N//3, N//2)
>>> np.allclose(y_p, x[N//3:N//2])
True