bilinear#
- scipy.signal.bilinear(b, a, fs=1.0)[Quelle]#
Berechnet ein digitales IIR-Filter aus einer analogen Übertragungsfunktion mithilfe der bilinearen Transformation.
- Parameter:
- barray_like
Koeffizienten des Zählerpolynoms der analogen Übertragungsfunktion in Form eines komplexen oder reellwertigen 1D-Arrays.
- aarray_like
Koeffizienten des Nennerpolynoms der analogen Übertragungsfunktion in Form eines komplexen oder reellwertigen 1D-Arrays.
- fsfloat
Abtastrate, als normale Frequenz (z. B. Hertz). In dieser Funktion findet keine Vorkorrektur statt.
- Rückgabe:
- betandarray
Koeffizienten des Zählerpolynoms der digitalen Übertragungsfunktion in Form eines komplexen oder reellwertigen 1D-Arrays.
- alphandarray
Koeffizienten des Nennerpolynoms der digitalen Übertragungsfunktion in Form eines komplexen oder reellwertigen 1D-Arrays.
Siehe auch
lp2lp,lp2hp,lp2bp,lp2bs,bilinear_zpk
Hinweise
Die Parameter \(b = [b_0, \ldots, b_Q]\) und \(a = [a_0, \ldots, a_P]\) sind 1D-Arrays der Länge \(Q+1\) und \(P+1\). Sie definieren die analoge Übertragungsfunktion
\[H_a(s) = \frac{b_0 s^Q + b_1 s^{Q-1} + \cdots + b_Q}{ a_0 s^P + a_1 s^{P-1} + \cdots + a_P}\ .\]Die bilineare Transformation [1] wird durch Substitution angewendet
\[s = \kappa \frac{z-1}{z+1}\ , \qquad \kappa := 2 f_s\ ,\]in \(H_a(s)\), wobei \(f_s\) die Abtastrate ist. Dies ergibt die digitale Übertragungsfunktion im \(z\)-Bereich
\[H_d(z) = \frac{b_0 \left(\kappa \frac{z-1}{z+1}\right)^Q + b_1 \left(\kappa \frac{z-1}{z+1}\right)^{Q-1} + \cdots + b_Q}{ a_0 \left(\kappa \frac{z-1}{z+1}\right)^P + a_1 \left(\kappa \frac{z-1}{z+1}\right)^{P-1} + \cdots + a_P}\ .\]Dieser Ausdruck kann vereinfacht werden, indem Zähler und Nenner mit \((z+1)^N\) multipliziert werden, wobei \(N=\max(P, Q)\). Dies ermöglicht es, \(H_d(z)\) wie folgt umzuformulieren:
\[\begin{split}& & \frac{b_0 \big(\kappa (z-1)\big)^Q (z+1)^{N-Q} + b_1 \big(\kappa (z-1)\big)^{Q-1} (z+1)^{N-Q+1} + \cdots + b_Q(z+1)^N}{ a_0 \big(\kappa (z-1)\big)^P (z+1)^{N-P} + a_1 \big(\kappa (z-1)\big)^{P-1} (z+1)^{N-P+1} + \cdots + a_P(z+1)^N}\\ &=:& \frac{\beta_0 + \beta_1 z^{-1} + \cdots + \beta_N z^{-N}}{ \alpha_0 + \alpha_1 z^{-1} + \cdots + \alpha_N z^{-N}}\ .\end{split}\]Dies ist die implementierte Gleichung zur Durchführung der bilinearen Transformation. Beachten Sie, dass bei großen \(f_s\) \(\kappa^Q\) oder \(\kappa^P\) bei ausreichend großen \(P\) oder \(Q\) zu einem numerischen Überlauf führen können.
Referenzen
Beispiele
Das folgende Beispiel zeigt den Frequenzgang eines analogen Bandpassfilters und des entsprechenden digitalen Filters, der durch die bilineare Transformation abgeleitet wurde.
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import numpy as np ... >>> fs = 100 # sampling frequency >>> om_c = 2 * np.pi * np.array([7, 13]) # corner frequencies >>> bb_s, aa_s = signal.butter(4, om_c, btype='bandpass', analog=True, output='ba') >>> bb_z, aa_z = signal.bilinear(bb_s, aa_s, fs) ... >>> w_z, H_z = signal.freqz(bb_z, aa_z) # frequency response of digitial filter >>> w_s, H_s = signal.freqs(bb_s, aa_s, worN=w_z*fs) # analog filter response ... >>> f_z, f_s = w_z * fs / (2*np.pi), w_s / (2*np.pi) >>> Hz_dB, Hs_dB = (20*np.log10(np.abs(H_).clip(1e-10)) for H_ in (H_z, H_s)) >>> fg0, ax0 = plt.subplots() >>> ax0.set_title("Frequency Response of 4-th order Bandpass Filter") >>> ax0.set(xlabel='Frequency $f$ in Hertz', ylabel='Magnitude in dB', ... xlim=[f_z[1], fs/2], ylim=[-200, 2]) >>> ax0.semilogx(f_z, Hz_dB, alpha=.5, label=r'$|H_z(e^{j 2 \pi f})|$') >>> ax0.semilogx(f_s, Hs_dB, alpha=.5, label=r'$|H_s(j 2 \pi f)|$') >>> ax0.legend() >>> ax0.grid(which='both', axis='x') >>> ax0.grid(which='major', axis='y') >>> plt.show()
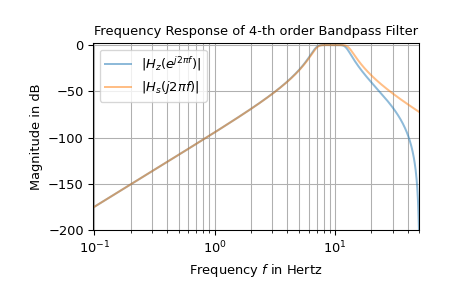
Der Unterschied in den höheren Frequenzen, der in der Darstellung gezeigt wird, ist auf einen Effekt namens „Frequenzkrümmung“ zurückzuführen. [1] beschreibt eine Methode namens „Vorkorrektur“, um diese Abweichungen zu reduzieren.