scipy.signal.

butter#

scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba', fs=None)[Quelle]#

Butterworth-Digital- und Analogfilterdesign.

Entwirft ein Butterworth-Filter der Ordnung N (digital oder analog) und gibt die Filterkoeffizienten zurück.

Parameter:

Nint

Die Ordnung des Filters. Für Bandpass- und Bandstopfilter ist die resultierende Ordnung der endgültigen Sektionen zweiter Ordnung („sos“) Matrix 2*N, wobei N die Anzahl der Biquad-Sektionen des gewünschten Systems ist.

Wnarray_like

Die Grenzfrequenz oder -frequenzen. Für Tiefpass- und Hochpassfilter ist Wn ein Skalar; für Bandpass- und Bandstopfilter ist Wn eine Sequenz der Länge 2.

Bei einem Butterworth-Filter ist dies der Punkt, an dem die Verstärkung auf 1/sqrt(2) der des Durchlassbereichs abfällt („-3 dB Punkt“).

Bei digitalen Filtern, wenn fs nicht angegeben ist, sind die Einheiten von Wn von 0 bis 1 normalisiert, wobei 1 die Nyquist-Frequenz ist (Wn ist somit in halben Zyklen/Sample und definiert als 2*kritische Frequenzen / fs). Wenn fs angegeben ist, ist Wn in denselben Einheiten wie fs.

Bei analogen Filtern ist Wn eine Winkelfrequenz (z. B. rad/s).

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional

Der Filtertyp. Standard ist ‘lowpass’.

analogbool, optional

Wenn True, wird ein analoger Filter zurückgegeben, andernfalls ein digitaler Filter.

output{‘ba’, ‘zpk’, ‘sos’}, optional

Typ der Ausgabe: Zähler/Nenner („ba“), Pol-Nullstelle („zpk“) oder Sektionen zweiter Ordnung („sos“). Standard ist „ba“ aus Gründen der Abwärtskompatibilität, aber „sos“ sollte für allgemeine Filterung verwendet werden.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems.

Hinzugefügt in Version 1.2.0.

Rückgabe:

b, andarray, ndarray: Zähler- (b) und Nenner- (a) Polynome des IIR-Filters. Nur zurückgegeben, wenn output='ba'.
z, p, kndarray, ndarray, float: Nullstellen, Pole und Systemverstärkung der Übertragungsfunktion des IIR-Filters. Nur zurückgegeben, wenn output='zpk'.
sosndarray: Zweistufige Abschnittsdarstellung des IIR-Filters. Nur zurückgegeben, wenn output='sos'.

Siehe auch

buttord, buttap

Hinweise

Der Butterworth-Filter hat eine maximal flache Frequenzantwort im Durchlassbereich.

Der Parameter output='sos' wurde in 0.16.0 hinzugefügt.

Wenn die Transferfunktionsform [b, a] angefordert wird, können numerische Probleme auftreten, da die Umwandlung zwischen Wurzeln und Polynomkoeffizienten eine numerisch empfindliche Operation ist, selbst für N >= 4. Es wird empfohlen, mit der SOS-Darstellung zu arbeiten.

Warnung

Das Entwerfen von Hochpass- und Schmalband-IIR-Filtern in TF-Form kann aufgrund von Problemen mit der Genauigkeit von Gleitkommaberechnungen zu instabilem oder falschem Filtern führen. Erwägen Sie die Überprüfung der Filtercharakteristiken mit freqz oder entwerfen Sie die Filter mit Sektionen zweiter Ordnung über output='sos'.

Beispiele

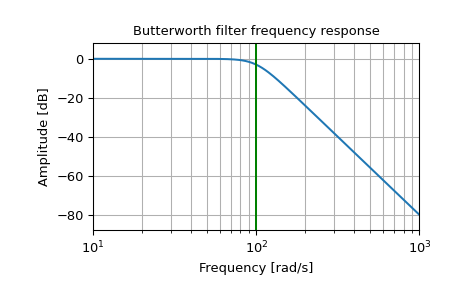
Entwurf eines analogen Filters und Darstellung seiner Frequenzgangkurve, wobei die kritischen Punkte gezeigt werden

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.butter(4, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Butterworth filter frequency response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green') # cutoff frequency
>>> plt.show()

../../_images/scipy-signal-butter-1_00_00.png

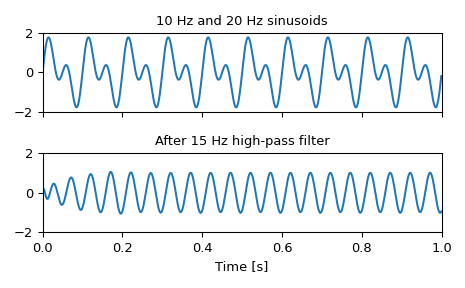
Generieren eines Signals, das aus 10 Hz und 20 Hz besteht, abgetastet mit 1 kHz

>>> t = np.linspace(0, 1, 1000, False)  # 1 second
>>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
>>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
>>> ax1.plot(t, sig)
>>> ax1.set_title('10 Hz and 20 Hz sinusoids')
>>> ax1.axis([0, 1, -2, 2])

Entwurf eines digitalen Hochpassfilters bei 15 Hz zur Entfernung des 10-Hz-Tons und Anwendung auf das Signal. (Es wird empfohlen, das Format der Sektionen zweiter Ordnung zum Filtern zu verwenden, um numerische Fehler im Transferfunktionsformat (ba) zu vermeiden)

>>> sos = signal.butter(10, 15, 'hp', fs=1000, output='sos')
>>> filtered = signal.sosfilt(sos, sig)
>>> ax2.plot(t, filtered)
>>> ax2.set_title('After 15 Hz high-pass filter')
>>> ax2.axis([0, 1, -2, 2])
>>> ax2.set_xlabel('Time [s]')
>>> plt.tight_layout()
>>> plt.show()

../../_images/scipy-signal-butter-1_01_00.png