scipy.signal.

freqz#

scipy.signal.freqz(b, a=1, worN=512, whole=False, plot=None, fs=6.283185307179586, include_nyquist=False)[Quelle]#

Berechnet die Frequenzantwort eines digitalen Filters.

Gegeben den Zähler b vom Grad M und den Nenner a vom Grad N eines digitalen Filters, berechne seine Frequenzantwort

            jw                 -jw              -jwM
   jw    B(e  )    b[0] + b[1]e    + ... + b[M]e
H(e  ) = ------ = -----------------------------------
            jw                 -jw              -jwN
         A(e  )    a[0] + a[1]e    + ... + a[N]e
Parameter:
barray_like

Zähler eines linearen Filters. Wenn b eine Dimension größer als 1 hat, wird angenommen, dass die Koeffizienten in der ersten Dimension gespeichert sind, und b.shape[1:], a.shape[1:] und die Form des Frequenzarrays müssen für das Broadcasting kompatibel sein.

aarray_like

Nenner eines linearen Filters. Wenn b eine Dimension größer als 1 hat, wird angenommen, dass die Koeffizienten in der ersten Dimension gespeichert sind, und b.shape[1:], a.shape[1:] und die Form des Frequenzarrays müssen für das Broadcasting kompatibel sein.

worN{None, int, array_like}, optional

Wenn eine einzelne Ganzzahl, dann berechne bei dieser Anzahl von Frequenzen (Standard ist N=512). Dies ist eine bequeme Alternative zu

np.linspace(0, fs if whole else fs/2, N, endpoint=include_nyquist)

Die Verwendung einer Zahl, die für FFT-Berechnungen schnell ist, kann zu schnelleren Berechnungen führen (siehe Hinweise).

Wenn ein Array-ähnlicher Wert, berechne die Antwort bei den gegebenen Frequenzen. Diese sind in denselben Einheiten wie fs.

wholebool, optional

Normalerweise werden die Frequenzen von 0 bis zur Nyquist-Frequenz, fs/2 (obere Hälfte des Einheitskreises), berechnet. Wenn whole True ist, berechne die Frequenzen von 0 bis fs. Ignoriert, wenn worN Array-ähnlich ist.

plotcallable

Ein aufrufbarer Wert, der zwei Argumente annimmt. Wenn angegeben, werden die Rückgabeparameter w und h an plot übergeben. Nützlich zum Plotten der Frequenzantwort innerhalb von freqz.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems. Standardmäßig 2*pi Radiant/Abtastung (also w von 0 bis pi).

Hinzugefügt in Version 1.2.0.

include_nyquistbool, optional

Wenn whole False ist und worN eine Ganzzahl ist, wird durch Setzen von include_nyquist auf True die letzte Frequenz (Nyquist-Frequenz) eingeschlossen und ansonsten ignoriert.

Hinzugefügt in Version 1.5.0.

Rückgabe:
wndarray

Die Frequenzen, bei denen h berechnet wurde, in denselben Einheiten wie fs. Standardmäßig wird w auf den Bereich [0, pi) (Radiant/Sample) normalisiert.

hndarray

Die Frequenzantwort als komplexe Zahlen.

Siehe auch

freqz_zpk
freqz_sos

Hinweise

Die Verwendung der Funktion matplotlib.pyplot.plot von Matplotlib als aufrufbarer Wert für plot führt zu unerwarteten Ergebnissen, da dies den Realteil der komplexen Übertragungsfunktion plottet und nicht die Amplitude. Versuchen Sie lambda w, h: plot(w, np.abs(h)).

Eine direkte Berechnung über (R)FFT wird verwendet, um die Frequenzantwort zu berechnen, wenn die folgenden Bedingungen erfüllt sind

  1. Für worN wird ein ganzzahliger Wert angegeben.

  2. worN ist durch FFT schnell zu berechnen (d.h. next_fast_len(worN) gleich worN).

  3. Die Nennerkoeffizienten sind ein einzelner Wert (a.shape[0] == 1).

  4. worN ist mindestens so lang wie die Zählerkoeffizienten (worN >= b.shape[0]).

  5. Wenn b.ndim > 1, dann ist b.shape[-1] == 1.

Für lange FIR-Filter kann der FFT-Ansatz einen geringeren Fehler aufweisen und viel schneller sein als die äquivalente direkte Polynomberechnung.

Beispiele

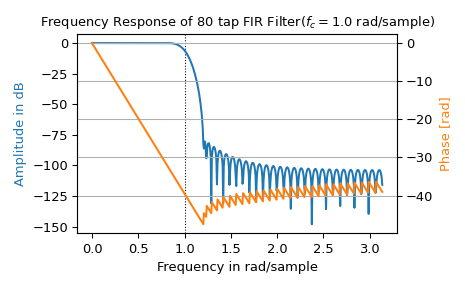
>>> from scipy import signal
>>> import numpy as np
>>> taps, f_c = 80, 1.0  # number of taps and cut-off frequency
>>> b = signal.firwin(taps, f_c, window=('kaiser', 8), fs=2*np.pi)
>>> w, h = signal.freqz(b)

>>> import matplotlib.pyplot as plt
>>> fig, ax1 = plt.subplots(tight_layout=True)
>>> ax1.set_title(f"Frequency Response of {taps} tap FIR Filter" +
...               f"($f_c={f_c}$ rad/sample)")
>>> ax1.axvline(f_c, color='black', linestyle=':', linewidth=0.8)
>>> ax1.plot(w, 20 * np.log10(abs(h)), 'C0')
>>> ax1.set_ylabel("Amplitude in dB", color='C0')
>>> ax1.set(xlabel="Frequency in rad/sample", xlim=(0, np.pi))

>>> ax2 = ax1.twinx()
>>> phase = np.unwrap(np.angle(h))
>>> ax2.plot(w, phase, 'C1')
>>> ax2.set_ylabel('Phase [rad]', color='C1')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> plt.show()
../../_images/scipy-signal-freqz-1_00_00.png

Broadcasting-Beispiele

Angenommen, wir haben zwei FIR-Filter, deren Koeffizienten in den Zeilen eines Arrays der Form (2, 25) gespeichert sind. Für diese Demonstration verwenden wir zufällige Daten

>>> rng = np.random.default_rng()
>>> b = rng.random((2, 25))

Um die Frequenzantwort für diese beiden Filter mit einem einzigen Aufruf von freqz zu berechnen, müssen wir b.T übergeben, da freqz erwartet, dass die erste Achse die Koeffizienten enthält. Wir müssen dann die Form mit einer trivialen Dimension der Länge 1 erweitern, um das Broadcasting mit dem Array der Frequenzen zu ermöglichen. Das heißt, wir übergeben b.T[..., np.newaxis], das die Form (25, 2, 1) hat

>>> w, h = signal.freqz(b.T[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)

Nehmen wir nun an, wir haben zwei Übertragungsfunktionen mit denselben Zählerkoeffizienten b = [0.5, 0.5]. Die Koeffizienten für die beiden Nenner sind in der ersten Dimension des 2-D-Arrays a gespeichert

a = [   1      1  ]
    [ -0.25, -0.5 ]

>>> b = np.array([0.5, 0.5])
>>> a = np.array([[1, 1], [-0.25, -0.5]])

Nur a ist mehr als 1-dimensional. Um es für das Broadcasting mit den Frequenzen kompatibel zu machen, erweitern wir es in dem Aufruf von freqz um eine triviale Dimension

>>> w, h = signal.freqz(b, a[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)
Auf dieser Seite