scipy.signal.

freqz_zpk#

scipy.signal.freqz_zpk(z, p, k, worN=512, whole=False, fs=6.283185307179586)[Quelle]#

Berechnet die Frequenzantwort eines digitalen Filters in ZPK-Form.

Gegeben die Nullstellen, Pole und den Verstärkungsfaktor eines digitalen Filters, berechnet seine Frequenzantwort

\(H(z)=k \prod_i (z - Z[i]) / \prod_j (z - P[j])\)

wobei \(k\) der Verstärkungsfaktor, \(Z\) die Nullstellen und \(P\) die Pole sind.

Parameter:

zarray_like

Nullstellen eines linearen Filters

parray_like

Pole eines linearen Filters

kSkalar

Verstärkungsfaktor eines linearen Filters

worN{None, int, array_like}, optional

Wenn eine einzelne Ganzzahl, dann Berechnung bei dieser Anzahl von Frequenzen (Standard ist N=512).

Wenn array_like, berechnet die Antwort bei den gegebenen Frequenzen. Diese sind in denselben Einheiten wie fs.

wholebool, optional

Normalerweise werden Frequenzen von 0 bis zur Nyquist-Frequenz, fs/2 (obere Hälfte des Einheitskreises) berechnet. Wenn whole True ist, werden Frequenzen von 0 bis fs berechnet. Wird ignoriert, wenn w array_like ist.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems. Standardmäßig 2*pi Radiant/Abtastung (also w von 0 bis pi).

Hinzugefügt in Version 1.2.0.

Rückgabe:

wndarray: Die Frequenzen, bei denen h berechnet wurde, in denselben Einheiten wie fs. Standardmäßig wird w auf den Bereich [0, pi) (Radiant/Sample) normalisiert.
hndarray: Die Frequenzantwort als komplexe Zahlen.

Siehe auch

freqs: Berechnet die Frequenzantwort eines analogen Filters in TF-Form
freqs_zpk: Berechnet die Frequenzantwort eines analogen Filters in ZPK-Form
freqz: Berechnet die Frequenzantwort eines digitalen Filters in TF-Form

Hinweise

Hinzugefügt in Version 0.19.0.

Beispiele

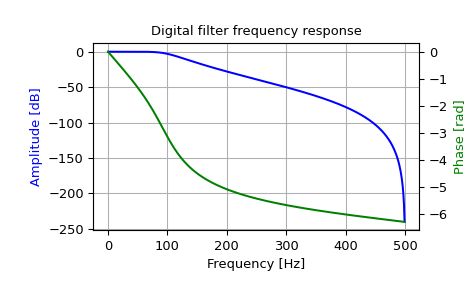
Entwirft einen digitalen Butterworth-Filter 4. Ordnung mit einer Grenzfrequenz von 100 Hz in einem System mit einer Abtastrate von 1000 Hz und plottet die Frequenzantwort

>>> import numpy as np
>>> from scipy import signal
>>> z, p, k = signal.butter(4, 100, output='zpk', fs=1000)
>>> w, h = signal.freqz_zpk(z, p, k, fs=1000)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 1, 1)
>>> ax1.set_title('Digital filter frequency response')

>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [Hz]')
>>> ax1.grid(True)

>>> ax2 = ax1.twinx()
>>> phase = np.unwrap(np.angle(h))
>>> ax2.plot(w, phase, 'g')
>>> ax2.set_ylabel('Phase [rad]', color='g')

>>> plt.axis('tight')
>>> plt.show()

../../_images/scipy-signal-freqz_zpk-1.png