scipy.signal.

iircomb

scipy.signal.iircomb(w0, Q, ftype='notch', fs=2.0, *, pass_zero=False)

Entwirft einen digitalen IIR-Kammfilter zum Kerben oder Spitzen.

Ein Kerb-Kammfilter besteht aus regelmäßig beabstandeten Bandstoppfiltern mit einer engen Bandbreite (hoher Gütefaktor). Jeder unterdrückt ein schmales Frequenzband und lässt den Rest des Spektrums wenig verändert.

Ein Spitzen-Kammfilter besteht aus regelmäßig beabstandeten Bandpassfiltern mit einer engen Bandbreite (hoher Gütefaktor). Jeder unterdrückt Komponenten außerhalb eines schmalen Frequenzbandes.

Parameter:

w0float

Die Grundfrequenz des Kammfilters (der Abstand zwischen seinen Spitzen). Diese muss die Abtastfrequenz gleichmäßig teilen. Wenn fs angegeben ist, ist dies in denselben Einheiten wie fs. Standardmäßig ist es ein normalisierter Skalar, der 0 < w0 < 1 erfüllen muss, wobei w0 = 1 der halben Abtastfrequenz entspricht.

Qfloat

Gütefaktor. Dimensionsloser Parameter, der die -3 dB Bandbreite bw eines Kerbfilters relativ zu seiner Mittenfrequenz charakterisiert, Q = w0/bw.

ftype{‘notch’, ‘peak’}

Der Typ des von der Funktion generierten Kammfilters. Wenn „notch“, dann gilt der Q-Faktor für die Kerben. Wenn „peak“, dann gilt der Q-Faktor für die Spitzen. Standard ist „notch“.

fsfloat, optional

Die Abtastfrequenz des Signals. Standard ist 2,0.

pass_zerobool, optional

Wenn False (Standard), sind die Kerben (Nullstellen) des Filters auf den Frequenzen [0, w0, 2*w0, …] zentriert und die Spitzen auf den Mittelpunkten [w0/2, 3*w0/2, 5*w0/2, …]. Wenn True, sind die Spitzen auf [0, w0, 2*w0, …] zentriert (Passieren der Nullfrequenz) und umgekehrt.

Hinzugefügt in Version 1.9.0.

Rückgabe:

b, andarray, ndarray

Zähler- (b) und Nenner- (a) Polynome des IIR-Filters.

Löst aus:

ValueError

Wenn w0 kleiner oder gleich 0 oder größer oder gleich fs/2 ist, wenn fs nicht durch w0 teilbar ist, wenn ftype nicht „notch“ oder „peak“ ist

Siehe auch

iirnotch

iirpeak

Hinweise

Details zur Implementierung siehe [1]. Die TF-Implementierung des Kammfilters ist auch bei höheren Ordnungen numerisch stabil, da ein einzelner wiederholter Pol verwendet wird, der keine Präzisionsverluste erleidet.

Referenzen

[1]

Sophocles J. Orfanidis, „Introduction To Signal Processing“, Prentice-Hall, 1996, Kap. 11, „Digital Filter Design“

Beispiele

Probieren Sie es in Ihrem Browser aus!

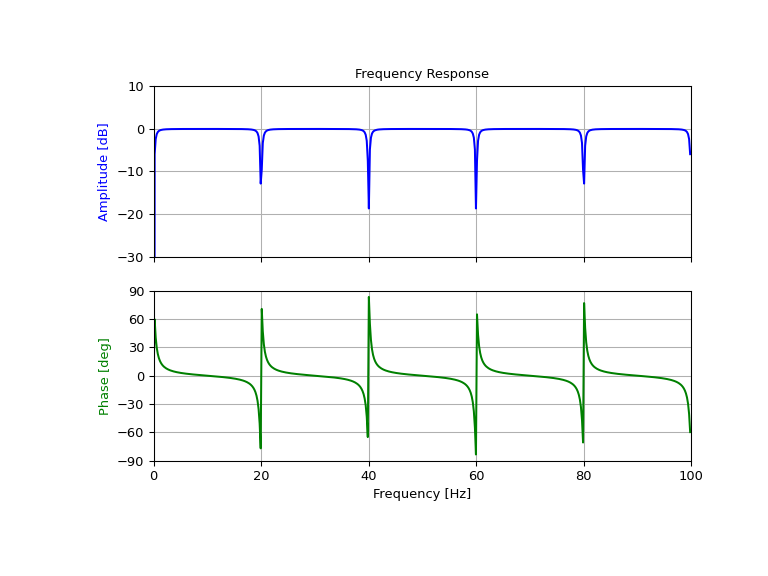
Entwerfen und Plotten eines Kerb-Kammfilters bei 20 Hz für ein Signal, das mit 200 Hz abgetastet wird, unter Verwendung eines Gütefaktors Q = 30

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> fs = 200.0  # Sample frequency (Hz)
>>> f0 = 20.0  # Frequency to be removed from signal (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design notching comb filter
>>> b, a = signal.iircomb(f0, Q, ftype='notch', fs=fs)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> response = abs(h)
>>> # To avoid divide by zero when graphing
>>> response[response == 0] = 1e-20
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6), sharex=True)
>>> ax[0].plot(freq, 20*np.log10(abs(response)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude [dB]", color='blue')
>>> ax[0].set_xlim([0, 100])
>>> ax[0].set_ylim([-30, 10])
>>> ax[0].grid(True)
>>> ax[1].plot(freq, (np.angle(h)*180/np.pi+180)%360 - 180, color='green')
>>> ax[1].set_ylabel("Phase [deg]", color='green')
>>> ax[1].set_xlabel("Frequency [Hz]")
>>> ax[1].set_xlim([0, 100])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid(True)
>>> plt.show()

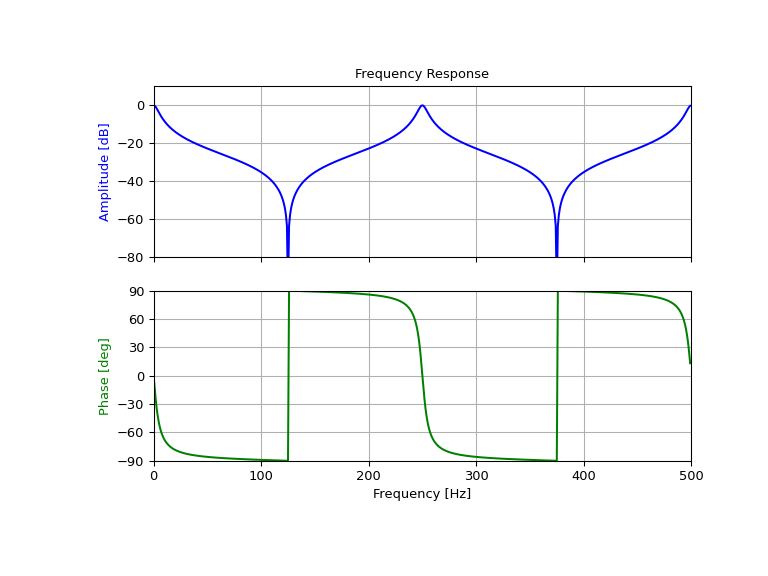
Entwerfen und Plotten eines Spitzen-Kammfilters bei 250 Hz für ein Signal, das mit 1000 Hz abgetastet wird, unter Verwendung eines Gütefaktors Q = 30

>>> fs = 1000.0  # Sample frequency (Hz)
>>> f0 = 250.0  # Frequency to be retained (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design peaking filter
>>> b, a = signal.iircomb(f0, Q, ftype='peak', fs=fs, pass_zero=True)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> response = abs(h)
>>> # To avoid divide by zero when graphing
>>> response[response == 0] = 1e-20
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6), sharex=True)
>>> ax[0].plot(freq, 20*np.log10(np.maximum(abs(h), 1e-5)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude [dB]", color='blue')
>>> ax[0].set_xlim([0, 500])
>>> ax[0].set_ylim([-80, 10])
>>> ax[0].grid(True)
>>> ax[1].plot(freq, (np.angle(h)*180/np.pi+180)%360 - 180, color='green')
>>> ax[1].set_ylabel("Phase [deg]", color='green')
>>> ax[1].set_xlabel("Frequency [Hz]")
>>> ax[1].set_xlim([0, 500])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid(True)
>>> plt.show()

ZurückIn Tab öffnen