scipy.signal.

periodogram#

scipy.signal.periodogram(x, fs=1.0, window='boxcar', nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1)[Quelle]#

Leistungsspektraldichte mittels Periodogramm schätzen.

Parameter:

xarray_like: Zeitreihen von Messwerten
fsfloat, optional: Abtastfrequenz der Zeitreihe x. Standardwert ist 1.0.
windowstr oder Tupel oder Array_like, optional: Gewünschtes Fenster zur Verwendung. Wenn window ein String oder Tupel ist, wird es an get_window übergeben, um die Fensterwerte zu generieren, die standardmäßig DFT-gerade sind. Siehe get_window für eine Liste von Fenstern und erforderliche Parameter. Wenn window array_like ist, wird es direkt als Fenster verwendet und seine Länge muss gleich der Länge der Achse sein, über die das Periodogramm berechnet wird. Standardwert ist 'boxcar'.
nfftint, optional: Länge der verwendeten FFT. Wenn None ist, wird die Länge von x verwendet.
detrendstr oder Funktion oder False, optional: Gibt an, wie jedes Segment entzerrt werden soll. Wenn detrend eine Zeichenkette ist, wird sie als Argument type an die Funktion detrend übergeben. Wenn es sich um eine Funktion handelt, nimmt sie ein Segment entgegen und gibt ein entzerrtes Segment zurück. Wenn detrend False ist, wird keine Entzerrung durchgeführt. Standard ist 'constant'.
return_onesidedbool, optional: Wenn True, wird ein einseitiges Spektrum für reale Daten zurückgegeben. Wenn False, wird ein zweiseitiges Spektrum zurückgegeben. Standard ist True, aber für komplexe Daten wird immer ein zweiseitiges Spektrum zurückgegeben.
scaling{ ‘density’, ‘spectrum’ }, optional: Wählt zwischen der Berechnung der Leistungsspektraldichte ('density'), bei der Pxx die Einheit V²/Hz hat, und der Berechnung des quadrierten Betazitätenspektrums ('spectrum'), bei der Pxx die Einheit V² hat, wenn x in V und fs in Hz gemessen wird. Standardwert ist 'density'.
axisint, optional: Achse, entlang der das Periodogramm berechnet wird; die Standardeinstellung ist die letzte Achse (d. h. axis=-1).

Rückgabe:

fndarray: Array von Abtastfrequenzen.
Pxxndarray: Leistungsspektraldichte oder Leistungsspektrum von x.

Siehe auch

welch: Schätzung der Leistungsspektraldichte mittels Welch-Methode
lombscargle: Lomb-Scargle-Periodogramm für ungleichmäßig abgetastete Daten

Hinweise

Das Verhältnis des quadrierten Betazes (scaling='spectrum') geteilt durch die spektrale Leistungsdichte (scaling='density') ist der konstante Faktor sum(abs(window)**2)*fs / abs(sum(window))**2. Wenn return_onesided True ist, werden die Werte der negativen Frequenzen zu den Werten der entsprechenden positiven addiert.

Konsultieren Sie den Abschnitt Spektralanalyse im SciPy Benutzerhandbuch für eine Diskussion der Skalierungen der Leistungsspektraldichte und des (quadrierten) Betazitätenspektrums.

Hinzugefügt in Version 0.12.0.

Beispiele

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Generieren Sie ein Testsignal, eine Sinuswelle mit 2 Veff bei 1234 Hz, korrumpiert durch weißes Rauschen mit 0,001 V²/Hz, abgetastet mit 10 kHz.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2*np.sqrt(2)
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> x = amp*np.sin(2*np.pi*freq*time)
>>> x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)

Berechnen und plotten Sie die Leistungsspektraldichte.

>>> f, Pxx_den = signal.periodogram(x, fs)
>>> plt.semilogy(f, Pxx_den)
>>> plt.ylim([1e-7, 1e2])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('PSD [V**2/Hz]')
>>> plt.show()

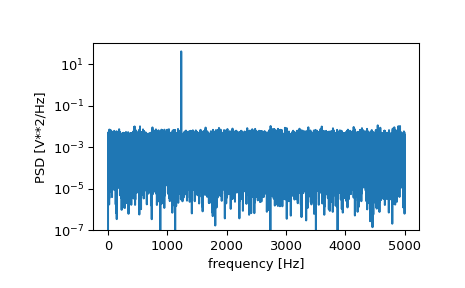
../../_images/scipy-signal-periodogram-1_00_00.png

Wenn wir die letzte Hälfte der Leistungsspektraldichte mitteln, um den Peak auszuschließen, können wir die Rauschleistung auf dem Signal wiederherstellen.

>>> np.mean(Pxx_den[25000:])
0.000985320699252543

Berechnen und plotten Sie nun das Leistungsspektrum.

>>> f, Pxx_spec = signal.periodogram(x, fs, 'flattop', scaling='spectrum')
>>> plt.figure()
>>> plt.semilogy(f, np.sqrt(Pxx_spec))
>>> plt.ylim([1e-4, 1e1])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Linear spectrum [V RMS]')
>>> plt.show()

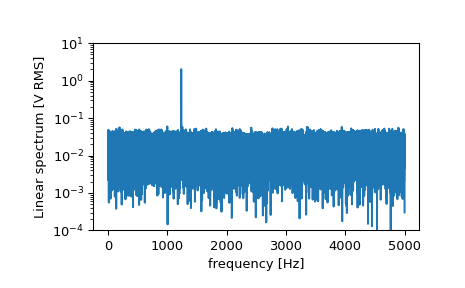
../../_images/scipy-signal-periodogram-1_01_00.png

Die Peak-Höhe im Leistungsspektrum ist eine Schätzung der Effektivwert-Amplitude.

>>> np.sqrt(Pxx_spec.max())
2.0077340678640727