scipy.signal.

remez

scipy.signal.remez(numtaps, bands, desired, *, weight=None, type='bandpass', maxiter=25, grid_density=16, fs=None)

Berechnet den minimax-optimalen Filter mittels des Remez-Austauschalgorithmus.

Berechnet die Filterkoeffizienten für einen FIR-Filter (Finite Impulse Response), dessen Übertragungsfunktion den maximalen Fehler zwischen dem gewünschten und dem realisierten Gain in den angegebenen Frequenzbändern mittels des Remez-Austauschalgorithmus minimiert.

Parameter:

numtapsint

Die gewünschte Anzahl von Taps im Filter. Die Anzahl der Taps ist die Anzahl der Terme im Filter oder die Filterordnung plus eins.

bandsarray_like

Eine monotone Sequenz, die die Bandkanten enthält. Alle Elemente müssen nicht-negativ und kleiner als die Hälfte der Abtastfrequenz, wie durch fs gegeben, sein.

desiredarray_like

Eine Sequenz, die halb so groß wie bands ist und den gewünschten Gain in jedem der angegebenen Bänder enthält.

weightarray_like, optional

Eine relative Gewichtung, die jedem Bandbereich zugewiesen wird. Die Länge von weight muss halb so groß sein wie die Länge von bands.

type{‘bandpass’, ‘differentiator’, ‘hilbert’}, optional

Der Typ des Filters

• ‘bandpass’ : flache Antwort in den Bändern. Dies ist der Standard.

• ‘differentiator’ : Frequenzproportionale Antwort in den Bändern.

• ‘hilbert’Filter mit ungerader Symmetrie, d.h. Typ III

  (für gerade Ordnung) oder Typ IV (für ungerade Ordnung) lineare Phasfilter.

maxiterint, optional

Maximale Anzahl von Iterationen des Algorithmus. Standard ist 25.

grid_densityint, optional

Gitterdichte. Das dichte Gitter, das in remez verwendet wird, hat die Größe (numtaps + 1) * grid_density. Standard ist 16.

fsfloat, optional

Die Abtastfrequenz des Signals. Standard ist 1.

Rückgabe:

outndarray

Ein Rang-1-Array, das die Koeffizienten des optimalen Filters (im Minimax-Sinne) enthält.

Siehe auch

firls

firwin

firwin2

minimum_phase

Referenzen

[1]

J. H. McClellan und T. W. Parks, „A unified approach to the design of optimum FIR linear phase digital filters“, IEEE Trans. Circuit Theory, Bd. CT-20, S. 697-701, 1973.

[2]

J. H. McClellan, T. W. Parks und L. R. Rabiner, „A Computer Program for Designing Optimum FIR Linear Phase Digital Filters“, IEEE Trans. Audio Electroacoust., Bd. AU-21, S. 506-525, 1973.

Beispiele

Probieren Sie es in Ihrem Browser aus!

In diesen Beispielen wird remez zur Entwicklung von Tiefpass-, Hochpass-, Bandpass- und Bandsperrfiltern verwendet. Die Parameter, die jeden Filter definieren, sind die Filterordnung, die Bandgrenzen, die Übergangsbreiten der Grenzen, die gewünschten Gains in jedem Band und die Abtastfrequenz.

Wir verwenden in allen Beispielen eine Abtastfrequenz von 22050 Hz. In jedem Beispiel ist der gewünschte Gain in jedem Band entweder 0 (für ein Sperrband) oder 1 (für ein Durchlassband).

freqz wird verwendet, um die Frequenzantwort jedes Filters zu berechnen, und die Hilfsfunktion plot_response, die unten definiert ist, wird verwendet, um die Antwort zu plotten.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> fs = 22050   # Sample rate, Hz

>>> def plot_response(w, h, title):
...     "Utility function to plot response functions"
...     fig = plt.figure()
...     ax = fig.add_subplot(111)
...     ax.plot(w, 20*np.log10(np.abs(h)))
...     ax.set_ylim(-40, 5)
...     ax.grid(True)
...     ax.set_xlabel('Frequency (Hz)')
...     ax.set_ylabel('Gain (dB)')
...     ax.set_title(title)

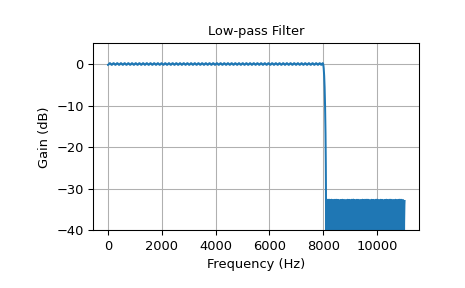
Das erste Beispiel ist ein Tiefpassfilter mit einer Grenzfrequenz von 8 kHz. Die Filterlänge beträgt 325 und die Übergangsbreite vom Durchlass- zum Sperrband beträgt 100 Hz.

>>> cutoff = 8000.0    # Desired cutoff frequency, Hz
>>> trans_width = 100  # Width of transition from pass to stop, Hz
>>> numtaps = 325      # Size of the FIR filter.
>>> taps = signal.remez(numtaps, [0, cutoff, cutoff + trans_width, 0.5*fs],
...                     [1, 0], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "Low-pass Filter")
>>> plt.show()

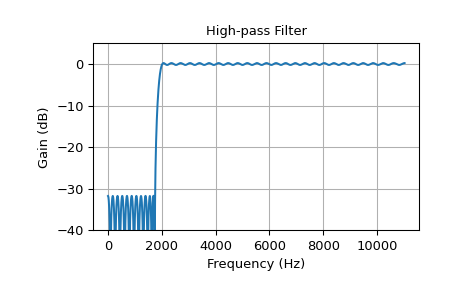
Dieses Beispiel zeigt einen Hochpassfilter

>>> cutoff = 2000.0    # Desired cutoff frequency, Hz
>>> trans_width = 250  # Width of transition from pass to stop, Hz
>>> numtaps = 125      # Size of the FIR filter.
>>> taps = signal.remez(numtaps, [0, cutoff - trans_width, cutoff, 0.5*fs],
...                     [0, 1], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "High-pass Filter")
>>> plt.show()

Dieses Beispiel zeigt einen Bandpassfilter mit einem Durchlassbereich von 2 kHz bis 5 kHz. Die Übergangsbreite beträgt 260 Hz und die Filterlänge beträgt 63, was kleiner ist als in den anderen Beispielen.

>>> band = [2000, 5000]  # Desired pass band, Hz
>>> trans_width = 260    # Width of transition from pass to stop, Hz
>>> numtaps = 63         # Size of the FIR filter.
>>> edges = [0, band[0] - trans_width, band[0], band[1],
...          band[1] + trans_width, 0.5*fs]
>>> taps = signal.remez(numtaps, edges, [0, 1, 0], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "Band-pass Filter")
>>> plt.show()

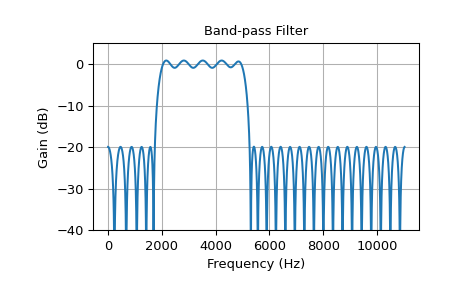
Die geringe Ordnung führt zu stärkerem Rippling und weniger steilen Übergängen.

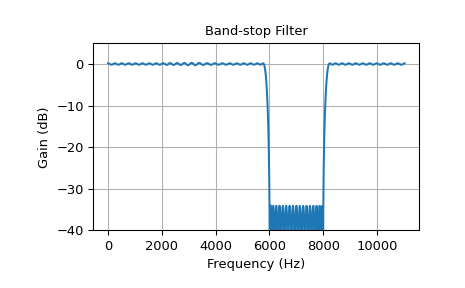
Das nächste Beispiel zeigt einen Bandsperrfilter.

>>> band = [6000, 8000]  # Desired stop band, Hz
>>> trans_width = 200    # Width of transition from pass to stop, Hz
>>> numtaps = 175        # Size of the FIR filter.
>>> edges = [0, band[0] - trans_width, band[0], band[1],
...          band[1] + trans_width, 0.5*fs]
>>> taps = signal.remez(numtaps, edges, [1, 0, 1], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "Band-stop Filter")
>>> plt.show()

ZurückIn Tab öffnen