scipy.signal.

resample

scipy.signal.resample(x, num, t=None, axis=0, window=None, domain='time')

Resample x auf num Samples mittels der Fourier-Methode entlang der gegebenen axis.

Die Resampling erfolgt durch Verkürzung oder Nullauffüllung der FFT von x. Dies hat die Vorteile eines idealen Antialiasing-Filters und erlaubt beliebige Auf- oder Abwärtsabtastraten. Der Hauptnachteil ist die Annahme, dass x ein periodisches Signal ist.

Parameter:

xarray_like

Das Eingabesignal besteht aus äquidistanten Abtastwerten. Wenn x ein mehrdimensionales Array ist, spezifiziert der Parameter axis die Zeit-/Frequenzachse. Es wird hier angenommen, dass n_x = x.shape[axis] die Anzahl der Samples und T das Abtastintervall angibt.

numint

Die Anzahl der Samples des resampelten Ausgangssignals. Sie kann größer oder kleiner als n_x sein.

tarray_like, optional

Wenn t nicht None ist, werden auch die Zeitstempel des resampelten Signals zurückgegeben. t muss mindestens die ersten beiden Zeitstempel des Eingangssignals x enthalten (alle anderen werden ignoriert). Die Zeitstempel des Ausgangssignals werden bestimmt durch t[0] + T * n_x / num * np.arange(num) mit T = t[1] - t[0]. Standard ist None.

axisint, optional

Die Zeit-/Frequenzachse von x, entlang der das Resampling stattfindet. Standard ist 0.

windowarray_like, callable, string, float, or tuple, optional

Wenn nicht None, gibt es einen Filter im Fourier-Bereich an, der vor dem Resampling angewendet wird. D.h., die FFT X von x wird berechnet durch X = W * fft(x, axis=axis). W kann als spektrale Fensterfunktion W(f_X) interpretiert werden, welche die Frequenzen f_X = fftfreq(n_x, T) konsumiert.

Wenn window ein 1D-Array der Länge n_x ist, dann ist W=window. Wenn window ein Callable ist, dann ist W = window(f_X). Andernfalls wird window an get_window übergeben, d.h. W = fftshift(signal.get_window(window, n_x)). Standard ist None.

domain‘time’ | ‘freq’, optional

Wenn auf 'time' (Standard) gesetzt, wird eine FFT auf x angewendet, andernfalls (bei 'freq') wird angenommen, dass bereits eine FFT angewendet wurde, d.h. x = fft(x_t, axis=axis) mit x_t als Eingangssignal im Zeitbereich.

Rückgabe:

x_rndarray

Das resampelte Signal, bestehend aus num Samples und dem Abtastintervall T * n_x / num.

t_rndarray, optional

Die num äquidistanten Zeitstempel von x_r. Dies wird nur zurückgegeben, wenn der Parameter t nicht None ist.

Siehe auch

decimate

Abwärtsabtastung eines (periodischen/nicht-periodischen) Signals nach Anwendung eines FIR- oder IIR-Filters.

resample_poly

Resampling eines (periodischen/nicht-periodischen) Signals mittels Polyphasenfilterung und eines FIR-Filters.

Hinweise

Diese Funktion verwendet die effizientere einseitige FFT, d.h. rfft / irfft, wenn x reellwertig und im Zeitbereich ist. Andernfalls wird die zweiseitige FFT, d.h. fft / ifft, verwendet (alle FFT-Funktionen stammen aus dem Modul scipy.fft).

Wenn ein window auf ein reellwertiges x angewendet wird, wird die einseitige spektrale Fensterfunktion durch Mittelung der negativen und positiven Frequenzkomponente bestimmt. Dies stellt sicher, dass reellwertige Signale und komplexe Signale mit Null-Imaginärteil identisch behandelt werden. D.h., das Übergeben von x oder das Übergeben von x.astype(np.complex128) liefert dasselbe numerische Ergebnis.

Wenn die Anzahl der Ein- oder Ausgabesamples prim oder nur wenige Primfaktoren hat, kann diese Funktion aufgrund der Verwendung von FFTs langsam sein. Konsultieren Sie prev_fast_len und next_fast_len, um effiziente Signallängen zu ermitteln. Alternativ kann die Verwendung von resample_poly zur Berechnung eines Zwischensignals (wie im folgenden Beispiel gezeigt) zu erheblichen Geschwindigkeitssteigerungen führen.

resample ist für periodische Signale mit äquidistanten Abtastintervallen vorgesehen. Für nicht-periodische Signale kann resample_poly eine bessere Wahl sein. Konsultieren Sie das Modul scipy.interpolate für Methoden zum Resampling von Signalen mit nicht-konstanten Abtastintervallen.

Beispiele

Probieren Sie es in Ihrem Browser aus!

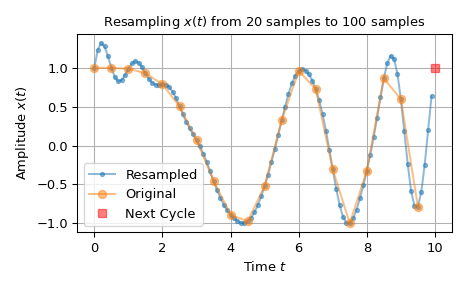
Das folgende Beispiel zeigt ein Signal, das von 20 auf 100 Samples hochskaliert wird. Das Klingeln am Anfang des hochskalierten Signals ist auf die Interpretation des periodischen Signals zurückzuführen. Das rote Quadrat in der Grafik veranschaulicht diese Periodizität, indem es das erste Sample des nächsten Zyklus des Signals zeigt.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import resample
...
>>> n0, n1 = 20, 100  # number of samples
>>> t0 = np.linspace(0, 10, n0, endpoint=False)  # input time stamps
>>> x0 = np.cos(-t0**2/6)  # input signal
...
>>> x1 = resample(x0, n1)  # resampled signal
>>> t1 = np.linspace(0, 10, n1, endpoint=False)  # timestamps of x1
...
>>> fig0, ax0 = plt.subplots(1, 1, tight_layout=True)
>>> ax0.set_title(f"Resampling $x(t)$ from {n0} samples to {n1} samples")
>>> ax0.set(xlabel="Time $t$", ylabel="Amplitude $x(t)$")
>>> ax0.plot(t1, x1, '.-', alpha=.5, label=f"Resampled")
>>> ax0.plot(t0, x0, 'o-', alpha=.5, label="Original")
>>> ax0.plot(10, x0[0], 'rs', alpha=.5, label="Next Cycle")
>>> ax0.legend(loc='best')
>>> ax0.grid(True)
>>> plt.show()

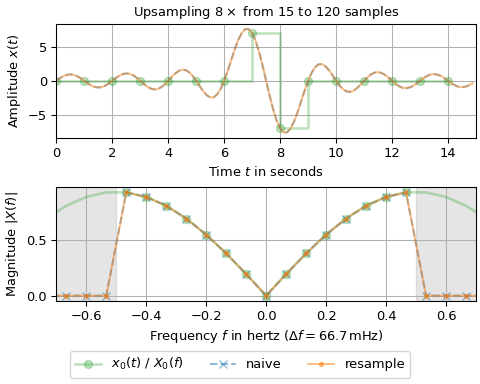
Das folgende Beispiel vergleicht diese Funktion mit einer naiven rfft / irfft-Kombination: Ein Eingangssignal mit einem Abtastintervall von einer Sekunde wird um den Faktor acht hochskaliert. Die erste Abbildung zeigt eine ungerade Anzahl von Eingangssamples, während die zweite Abbildung eine gerade Anzahl zeigt. Die oberen Teilgraphen zeigen die Signale über die Zeit: Die Eingangssamples sind durch große grüne Punkte markiert, die hochskalierten Signale durch eine durchgehende und eine gestrichelte Linie. Die unteren Teilgraphen zeigen das Amplitudenspektrum: Die FFT-Werte des Eingangs sind durch große grüne Punkte dargestellt, die im Frequenzintervall [-0,5, 0,5] Hz liegen, während das Frequenzintervall des hochskalierten Signals [-4, 4] Hz beträgt. Die durchgehende grüne Linie stellt das hochskalierte Spektrum ohne Antialiasing-Filter dar, welches eine periodische Fortsetzung des Eingangsspektrums ist. Die blauen Kreuze und orangen Punkte stellen die FFT-Werte des Signals dar, das mit dem naiven Ansatz sowie mit dem Ergebnis dieser Funktion erstellt wurde.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import fftshift, fftfreq, fft, rfft, irfft
>>> from scipy.signal import resample, resample_poly
... 
>>> fac, T0, T1 = 8, 1, 1/8  # upsampling factor and sampling intervals
>>> for n0 in (15, 16):  # number of samples of input signal
...     n1 = fac * n0  # number of samples of upsampled signal
...     t0, t1 = T0 * np.arange(n0), T1 * np.arange(n1)  # time stamps
...     x0 = np.zeros(n0)  # input signal has two non-zero sample values
...     x0[n0//2], x0[n0//2+1] = n0 // 2, -(n0 // 2)
... 
...     x1n = irfft(rfft(x0), n=n1) * n1 / n0  # naive resampling
...     x1r = resample(x0, n1)  # resample signal
... 
...     # Determine magnitude spectrum:
...     x0_up = np.zeros_like(x1r)  # upsampling without antialiasing filter
...     x0_up[::n1 // n0] = x0
...     X0, X0_up = (fftshift(fft(x_)) / n0 for x_ in (x0, x0_up))
...     XX1 = (fftshift(fft(x_)) / n1 for x_ in (x1n, x1r))
...     f0, f1 = fftshift(fftfreq(n0, T0)), fftshift(fftfreq(n1, T1))  # frequencies
...     df = f0[1] - f0[0]  # frequency resolution
... 
...     fig, (ax0, ax1) = plt.subplots(2, 1, layout='constrained', figsize=(5, 4))
...     ax0.set_title(rf"Upsampling ${fac}\times$ from {n0} to {n1} samples")
...     ax0.set(xlabel="Time $t$ in seconds", ylabel="Amplitude $x(t)$", 
...             xlim=(0, n1*T1))
...     ax0.step(t0, x0, 'C2o-', where='post', alpha=.3, linewidth=2, 
...              label="$x_0(t)$ / $X_0(f)$")
...     for x_, l_ in zip((x1n, x1r), ('C0--', 'C1-')):
...         ax0.plot(t1, x_, l_, alpha=.5, label=None)
...     ax0.grid()
...     ax1.set(xlabel=rf"Frequency $f$ in hertz ($\Delta f = {df*1e3:.1f}\,$mHz)", 
...             ylabel="Magnitude $|X(f)|$", xlim=(-0.7, 0.7))
...     ax1.axvspan(0.5/T0, f1[-1], color='gray', alpha=.2)
...     ax1.axvspan(f1[0], -0.5/T0, color='gray', alpha=.2)
...     ax1.plot(f1, abs(X0_up), 'C2-', f0, abs(X0),  'C2o', alpha=.3, linewidth=2)
...     for X_, n_, l_ in zip(XX1, ("naive", "resample"), ('C0x--', 'C1.-')): 
...         ax1.plot(f1, abs(X_), l_, alpha=.5, label=n_)
...     ax1.grid()
...     fig.legend(loc='outside lower center', ncols=4)    
>>> plt.show()

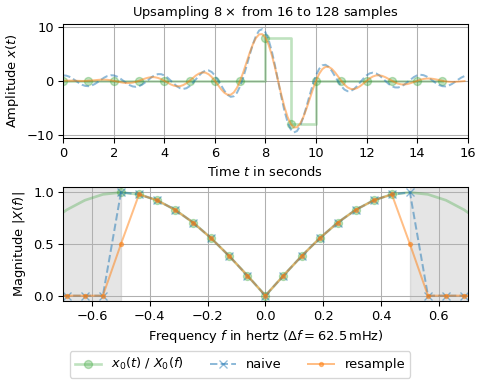
Die erste Abbildung zeigt, dass das Hochskalieren einer ungeraden Anzahl von Samples identische Ergebnisse liefert. Die zweite Abbildung veranschaulicht, dass das Signal, das mit dem naiven Ansatz (gestrichelte blaue Linie) aus einer geraden Anzahl von Samples erzeugt wird, nicht alle ursprünglichen Samples berührt. Diese Abweichung ist darauf zurückzuführen, dass resample gepaarte Frequenz-Bins korrekt behandelt. D.h., der Eingang x1 hat ein Bin-Paar bei ±0,5 Hz, während der Ausgang nur ein einzelnes Bin bei -0,5 Hz hat, was eine Neuskalierung dieses Bin-Paares erfordert. Im Allgemeinen ist eine spezielle Behandlung erforderlich, wenn n_x != num und min(n_x, num) gerade ist. Wenn die Bin-Werte bei ±m Null sind, ist offensichtlich keine spezielle Behandlung erforderlich. Konsultieren Sie den Quellcode von resample für Details.

Das letzte Beispiel zeigt, wie resample_poly zur Beschleunigung der Abwärtsabtastung verwendet werden kann: Das Eingangssignal hat einen Wert ungleich Null bei \(t=0\) und wird von 19937 auf 128 Samples abgetastet. Da 19937 eine Primzahl ist, wird erwartet, dass die FFT langsam ist. Um die Sache zu beschleunigen, wird resample_poly verwendet, um zuerst um einen Faktor von n0 // n1 = 155 abzutasten und dann das Ergebnis an resample zu übergeben. Zwei Parametrisierungen von resample_poly werden verwendet: Das Übergeben von padtype='wrap' behandelt den Eingang als periodisch, während die Standardparametrisierung eine Nullauffüllung durchführt. Der obere Teilgraph zeigt die resultierenden Signale über die Zeit, während der untere Teilgraph die resultierenden einseitigen Amplitudenspektren darstellt.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import rfftfreq, rfft
>>> from scipy.signal import resample, resample_poly
... 
>>> n0 = 19937 # number of input samples - prime
>>> n1 = 128  # number of output samples - fast FFT length
>>> T0, T1 = 1/n0, 1/n1  # sampling intervals
>>> t0, t1 = np.arange(n0)*T0, np.arange(n1)*T1  # time stamps
... 
>>> x0 = np.zeros(n0)  # Input has one non-zero sample
>>> x0[0] = n0
>>> 
>>> x1r = resample(x0, n1)  # slow due to n0 being prime
>>> # This is faster:
>>> x1p = resample(resample_poly(x0, 1, n0 // n1, padtype='wrap'), n1)  # periodic 
>>> x2p = resample(resample_poly(x0, 1, n0 // n1), n1)  # with zero-padding
... 
>>> X0 = rfft(x0) / n0 
>>> X1r, X1p, X2p = rfft(x1r) / n1, rfft(x1p) / n1, rfft(x2p) / n1
>>> f0, f1 = rfftfreq(n0, T0), rfftfreq(n1, T1)
... 
>>> fig, (ax0, ax1) = plt.subplots(2, 1, layout='constrained', figsize=(5, 4))
>>> ax0.set_title(f"Dowsampled Impulse response (from {n0} to {n1} samples)")
>>> ax0.set(xlabel="Time $t$ in seconds", ylabel="Amplitude $x(t)$", xlim=(-T1, 1)) 
>>> for x_ in (x1r, x1p, x2p):
...     ax0.plot(t1, x_, alpha=.5)
>>> ax0.grid()
>>> ax1.set(xlabel=rf"Frequency $f$ in hertz ($\Delta f = {f1[1]}\,$Hz)", 
...         ylabel="Magnitude $|X(f)|$", xlim=(0, 0.55/T1))
>>> ax1.axvspan(0.5/T1, f0[-1], color='gray', alpha=.2)
>>> ax1.plot(f1, abs(X1r), 'C0.-', alpha=.5, label="resample")
>>> ax1.plot(f1, abs(X1p), 'C1.-', alpha=.5, label="resample_poly(padtype='wrap')")
>>> ax1.plot(f1, abs(X2p), 'C2x-', alpha=.5, label="resample_poly")
>>> ax1.grid()
>>> fig.legend(loc='outside lower center', ncols=2)
>>> plt.show()    

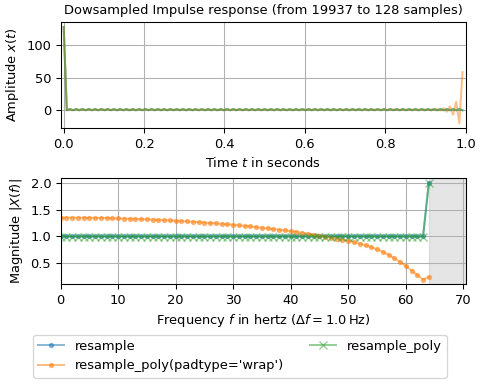
Die Graphen zeigen, dass die Ergebnisse der „reinen“ resample und der Verwendung der Standardparameter von resample_poly gut übereinstimmen. Die periodische Auffüllung von resample_poly (padtype='wrap') hingegen führt zu erheblichen Abweichungen. Dies liegt an der Diskontinuität am Anfang des Signals, für die der Standardfilter von resample_poly nicht gut geeignet ist. Dieses Beispiel veranschaulicht, dass für einige Anwendungsfälle die Anpassung der resample_poly-Parameter von Vorteil sein kann. resample hat hier einen großen Vorteil: Es verwendet standardmäßig den idealen Antialiasing-Filter mit der maximalen Bandbreite.

Beachten Sie, dass die verdoppelte Spektralmagnitude bei der Nyquist-Frequenz von 64 Hz auf die gerade Anzahl von n1=128 Ausgangssamples zurückzuführen ist, was eine Sonderbehandlung erfordert, wie im vorherigen Beispiel erläutert.

ZurückIn Tab öffnen