chebyu#
- scipy.special.chebyu(n, monic=False)[Quelle]#
Chebyshev-Polynom zweiter Art.
Definiert als die Lösung von
\[(1 - x^2)\frac{d^2}{dx^2}U_n - 3x\frac{d}{dx}U_n + n(n + 2)U_n = 0;\]\(U_n\) ist ein Polynom vom Grad \(n\).
- Parameter:
- nint
Grad des Polynoms.
- monicbool, optional
Wenn True, wird der führende Koeffizient auf 1 skaliert. Standard ist False.
- Rückgabe:
- Uorthopoly1d
Chebyshev-Polynom zweiter Art.
Siehe auch
chebytChebyshev-Polynom erster Art.
Hinweise
Die Polynome \(U_n\) sind orthogonal über \([-1, 1]\) mit der Gewichtungsfunktion \((1 - x^2)^{1/2}\).
Referenzen
[AS]Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.
Beispiele
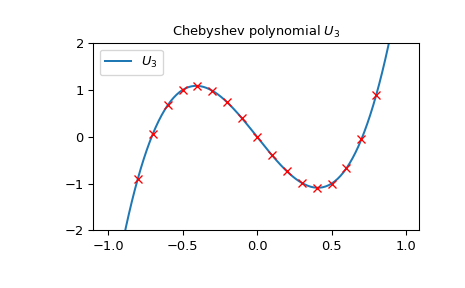
Chebyshev-Polynome zweiter Art der Ordnung \(n\) können als Determinante spezifischer \(n \times n\) Matrizen erhalten werden. Als Beispiel können wir überprüfen, wie die Punkte, die aus der Determinante der folgenden \(3 \times 3\) Matrix erhalten werden, exakt auf \(U_3\) liegen.
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.linalg import det >>> from scipy.special import chebyu >>> x = np.arange(-1.0, 1.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-2.0, 2.0) >>> ax.set_title(r'Chebyshev polynomial $U_3$') >>> ax.plot(x, chebyu(3)(x), label=rf'$U_3$') >>> for p in np.arange(-1.0, 1.0, 0.1): ... ax.plot(p, ... det(np.array([[2*p, 1, 0], [1, 2*p, 1], [0, 1, 2*p]])), ... 'rx') >>> plt.legend(loc='best') >>> plt.show()
Sie erfüllen die Rekursionsbeziehung
\[U_{2n-1}(x) = 2 T_n(x)U_{n-1}(x)\]wobei die \(T_n\) die Chebyshev-Polynome erster Art sind. Überprüfen wir dies für \(n = 2\).
>>> from scipy.special import chebyt >>> x = np.arange(-1.0, 1.0, 0.01) >>> np.allclose(chebyu(3)(x), 2 * chebyt(2)(x) * chebyu(1)(x)) True
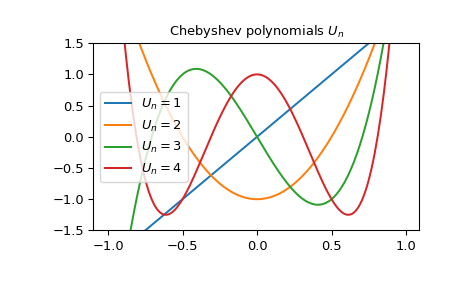
Wir können die Chebyshev-Polynome \(U_n\) für einige Werte von \(n\) plotten.
>>> x = np.arange(-1.0, 1.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-1.5, 1.5) >>> ax.set_title(r'Chebyshev polynomials $U_n$') >>> for n in np.arange(1,5): ... ax.plot(x, chebyu(n)(x), label=rf'$U_n={n}$') >>> plt.legend(loc='best') >>> plt.show()