scipy.special.erfcinv#

scipy.special.erfcinv(y, out=None) = <ufunc 'erfcinv'>#

Inverse der komplementären Fehlerfunktion.

Berechnet die Umkehrfunktion der komplementären Fehlerfunktion.

Im komplexen Bereich gibt es keine eindeutige komplexe Zahl w, die erfc(w)=z erfüllt. Dies deutet darauf hin, dass eine echte Umkehrfunktion mehrwertig wäre. Wenn die Domäne auf die reellen Zahlen beschränkt ist, 0 < x < 2, gibt es eine eindeutige reelle Zahl, die erfc(erfcinv(x)) = erfcinv(erfc(x)) erfüllt.

Sie steht zur Umkehrfunktion der Fehlerfunktion in Beziehung über erfcinv(1-x) = erfinv(x)

Parameter:

yndarray: Argument, an dem ausgewertet werden soll. Domäne: [0, 2]
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

erfcinvSkalar oder ndarray: Die Umkehrung von erfc von y, elementweise

Siehe auch

erf: Fehlerfunktion eines komplexen Arguments
erfc: Komplementäre Fehlerfunktion, 1 - erf(x)
erfinv: Inverse der Fehlerfunktion

Beispiele

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import erfcinv

>>> erfcinv(0.5)
0.4769362762044699

>>> y = np.linspace(0.0, 2.0, num=11)
>>> erfcinv(y)
array([        inf,  0.9061938 ,  0.59511608,  0.37080716,  0.17914345,
       -0.        , -0.17914345, -0.37080716, -0.59511608, -0.9061938 ,
              -inf])

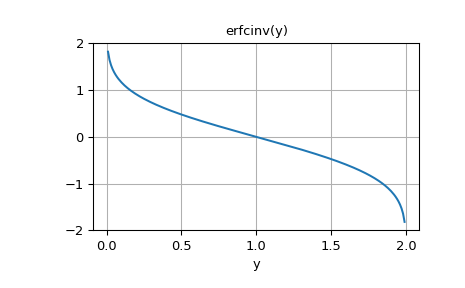
Zeichnen Sie die Funktion

>>> y = np.linspace(0, 2, 200)
>>> fig, ax = plt.subplots()
>>> ax.plot(y, erfcinv(y))
>>> ax.grid(True)
>>> ax.set_xlabel('y')
>>> ax.set_title('erfcinv(y)')
>>> plt.show()

../../_images/scipy-special-erfcinv-1.png