scipy.special.gdtr#

scipy.special.gdtr(a, b, x, out=None) = <ufunc 'gdtr'>#

Kumulative Verteilungsfunktion der Gamma-Verteilung.

Gibt das Integral von null bis x der Gamma-Wahrscheinlichkeitsdichtefunktion zurück,

\[F = \int_0^x \frac{a^b}{\Gamma(b)} t^{b-1} e^{-at}\,dt,\]

wobei \(\Gamma\) die Gamma-Funktion ist.

Parameter:

aarray_like: Der Ratenparameter der Gamma-Verteilung, manchmal als \(\beta\) bezeichnet (float). Er ist auch der Kehrwert des Skalenparameters \(\theta\).
barray_like: Der Formparameter der Gamma-Verteilung, manchmal als \(\alpha\) bezeichnet (float).
xarray_like: Das Quantil (obere Integrationsgrenze; float).
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

FSkalar oder ndarray: Die CDF der Gamma-Verteilung mit den Parametern a und b, ausgewertet an x.

Siehe auch

gdtrc: 1 - CDF der Gamma-Verteilung.
scipy.stats.gamma: Gamma-Verteilung

Hinweise

Die Auswertung erfolgt unter Verwendung der Beziehung zur unvollständigen Gamma-Funktion (regularisierte Gamma-Funktion).

Wrapper für die Cephes [1] Routine gdtr. Der direkte Aufruf von gdtr kann die Leistung im Vergleich zur cdf Methode von scipy.stats.gamma verbessern (siehe letztes Beispiel unten).

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Berechnet die Funktion für a=1, b=2 bei x=5.

>>> import numpy as np
>>> from scipy.special import gdtr
>>> import matplotlib.pyplot as plt
>>> gdtr(1., 2., 5.)
0.9595723180054873

Berechnet die Funktion für a=1 und b=2 an mehreren Punkten, indem ein NumPy-Array für x bereitgestellt wird.

>>> xvalues = np.array([1., 2., 3., 4])
>>> gdtr(1., 1., xvalues)
array([0.63212056, 0.86466472, 0.95021293, 0.98168436])

gdtr kann verschiedene Parametersätze auswerten, indem Arrays mit Broadcasting-kompatiblen Formen für a, b und x bereitgestellt werden. Hier berechnen wir die Funktion für drei verschiedene a an vier Positionen x und b=3, was zu einem 3x4-Array führt.

>>> a = np.array([[0.5], [1.5], [2.5]])
>>> x = np.array([1., 2., 3., 4])
>>> a.shape, x.shape
((3, 1), (4,))

>>> gdtr(a, 3., x)
array([[0.01438768, 0.0803014 , 0.19115317, 0.32332358],
       [0.19115317, 0.57680992, 0.82642193, 0.9380312 ],
       [0.45618688, 0.87534798, 0.97974328, 0.9972306 ]])

Plotten der Funktion für vier verschiedene Parametersätze.

>>> a_parameters = [0.3, 1, 2, 6]
>>> b_parameters = [2, 10, 15, 20]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(a_parameters, b_parameters, linestyles))
>>> x = np.linspace(0, 30, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     a, b, style = parameter_set
...     gdtr_vals = gdtr(a, b, x)
...     ax.plot(x, gdtr_vals, label=fr"$a= {a},\, b={b}$", ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> ax.set_title("Gamma distribution cumulative distribution function")
>>> plt.show()

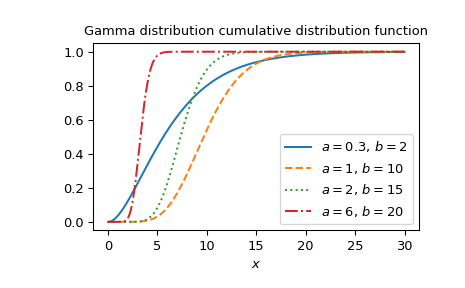
../../_images/scipy-special-gdtr-1_00_00.png

Die Gamma-Verteilung ist auch als scipy.stats.gamma verfügbar. Die direkte Verwendung von gdtr kann wesentlich schneller sein als der Aufruf der cdf Methode von scipy.stats.gamma, insbesondere für kleine Arrays oder einzelne Werte. Um die gleichen Ergebnisse zu erzielen, muss die folgende Parametrisierung verwendet werden: stats.gamma(b, scale=1/a).cdf(x)=gdtr(a, b, x).

>>> from scipy.stats import gamma
>>> a = 2.
>>> b = 3
>>> x = 1.
>>> gdtr_result = gdtr(a, b, x)  # this will often be faster than below
>>> gamma_dist_result = gamma(b, scale=1/a).cdf(x)
>>> gdtr_result == gamma_dist_result  # test that results are equal
True