scipy.special.

gegenbauer

scipy.special.gegenbauer(n, alpha, monic=False)

Gegenbauer (ultrasphärische) Polynome.

Definiert als die Lösung von

\[(1 - x^2)\frac{d^2}{dx^2}C_n^{(\alpha)} - (2\alpha + 1)x\frac{d}{dx}C_n^{(\alpha)} + n(n + 2\alpha)C_n^{(\alpha)} = 0\]

für \(\alpha > -1/2\); \(C_n^{(\alpha)}\) ist ein Polynom vom Grad \(n\).

Parameter:

nint

Grad des Polynoms.

alphafloat

Parameter, muss größer als -0,5 sein.

monicbool, optional

Wenn True, wird der führende Koeffizient auf 1 skaliert. Standard ist False.

Rückgabe:

Corthopoly1d

Gegenbauer-Polynom.

Hinweise

Die Polynome \(C_n^{(\alpha)}\) sind orthogonal über \([-1,1]\) mit der Gewichtungsfunktion \((1 - x^2)^{(\alpha - 1/2)}\).

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy import special
>>> import matplotlib.pyplot as plt

Wir können eine Variable p als Gegenbauer-Polynom mit der Funktion gegenbauer initialisieren und an einem Punkt x = 1 auswerten.

>>> p = special.gegenbauer(3, 0.5, monic=False)
>>> p
poly1d([ 2.5,  0. , -1.5,  0. ])
>>> p(1)
1.0

Um p an verschiedenen Punkten x im Intervall (-3, 3) auszuwerten, übergeben Sie einfach ein Array x wie folgt an p:

>>> x = np.linspace(-3, 3, 400)
>>> y = p(x)

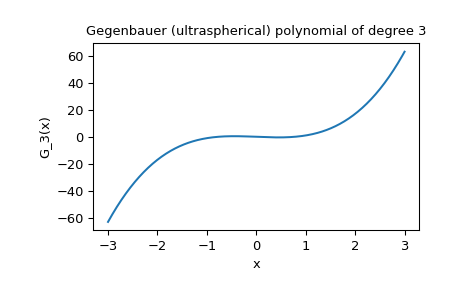
Wir können dann x, y mit matplotlib.pyplot visualisieren.

>>> fig, ax = plt.subplots()
>>> ax.plot(x, y)
>>> ax.set_title("Gegenbauer (ultraspherical) polynomial of degree 3")
>>> ax.set_xlabel("x")
>>> ax.set_ylabel("G_3(x)")
>>> plt.show()

ZurückIn Tab öffnen