scipy.special.k1e#

scipy.special.k1e(x, out=None) = <ufunc 'k1e'>#

Exponentiell skalierte modifizierte Bessel-Funktion K der Ordnung 1

Definiert als

k1e(x) = exp(x) * k1(x)

Parameter:

xarray_like: Argument (float)
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

Kscalar oder ndarray: Wert der exponentiell skalierten modifizierten Bessel-Funktion K der Ordnung 1 bei x.

Siehe auch

kv: Modifizierte Besselfunktion der zweiten Art beliebiger Ordnung
k1: Modifizierte Bessel-Funktion der zweiten Art der Ordnung 1

Hinweise

Der Bereich wird in die zwei Intervalle [0, 2] und (2, unendlich) aufgeteilt. In jedem Intervall werden Tschebyscheff-Polynom-Entwicklungen verwendet.

Diese Funktion ist ein Wrapper für die Cephes-Routine [1] k1e.

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Im folgenden Beispiel gibt k1 0 zurück, während k1e immer noch eine nützliche Gleitkommazahl zurückgibt.

>>> from scipy.special import k1, k1e
>>> k1(1000.), k1e(1000.)
(0., 0.03964813081296021)

Berechnen Sie die Funktion an mehreren Punkten, indem Sie ein NumPy-Array oder eine Liste für x angeben.

>>> import numpy as np
>>> k1e(np.array([0.5, 2., 3.]))
array([2.73100971, 1.03347685, 0.80656348])

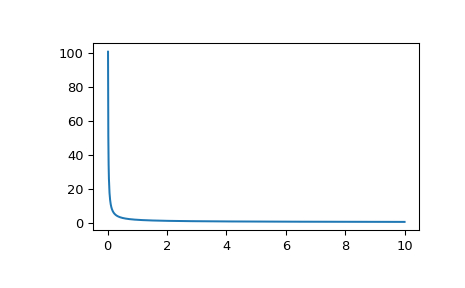
Plotten Sie die Funktion von 0 bis 10.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 10., 1000)
>>> y = k1e(x)
>>> ax.plot(x, y)
>>> plt.show()