spherical_yn#
- scipy.special.spherical_yn(n, z, derivative=False)[Quelle]#
Sphärische Besselfunktion zweiter Art oder ihre Ableitung.
Definiert als [1],
\[y_n(z) = \sqrt{\frac{\pi}{2z}} Y_{n + 1/2}(z),\]wobei \(Y_n\) die Besselfunktion zweiter Art ist.
- Parameter:
- nint, array_like
Ordnung der Besselfunktion (n >= 0).
- zcomplex oder float, array_like
Argument der Besselfunktion.
- derivativebool, optional
Wenn True, wird der Wert der Ableitung (anstelle der Funktion selbst) zurückgegeben.
- Rückgabe:
- ynndarray
Hinweise
Für reelle Argumente wird die Funktion mithilfe der aufsteigenden Rekurrenz [2] berechnet. Für komplexe Argumente wird die definitorische Beziehung zur zylindrischen Besselfunktion zweiter Art verwendet.
Die Ableitung wird mithilfe der Beziehungen [3] berechnet:
\[ \begin{align}\begin{aligned}y_n' = y_{n-1} - \frac{n + 1}{z} y_n.\\y_0' = -y_1\end{aligned}\end{align} \]Hinzugefügt in Version 0.18.0.
Referenzen
[AS]Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.
Beispiele
Die sphärischen Besselfunktionen zweiter Art \(y_n\) akzeptieren sowohl reelle als auch komplexe zweite Argumente. Sie können einen komplexen Typ zurückgeben.
>>> from scipy.special import spherical_yn >>> spherical_yn(0, 3+5j) (8.022343088587197-9.880052589376795j) >>> type(spherical_yn(0, 3+5j)) <class 'numpy.complex128'>
Wir können die Beziehung für die Ableitung anhand der Hinweise für \(n=3\) im Intervall \([1, 2]\) überprüfen.
>>> import numpy as np >>> x = np.arange(1.0, 2.0, 0.01) >>> np.allclose(spherical_yn(3, x, True), ... spherical_yn(2, x) - 4/x * spherical_yn(3, x)) True
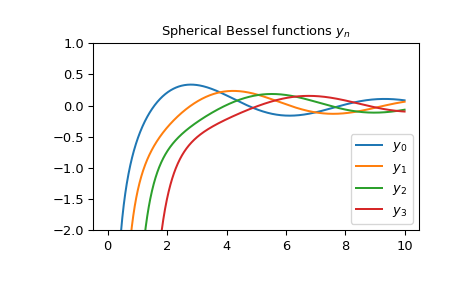
Die ersten paar \(y_n\) mit reellem Argument
>>> import matplotlib.pyplot as plt >>> x = np.arange(0.0, 10.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-2.0, 1.0) >>> ax.set_title(r'Spherical Bessel functions $y_n$') >>> for n in np.arange(0, 4): ... ax.plot(x, spherical_yn(n, x), label=rf'$y_{n}$') >>> plt.legend(loc='best') >>> plt.show()