scipy.special.stdtrit

scipy.special.stdtrit(df, p, out=None) = <ufunc 'stdtrit'>

Das p-te Quantil der Student-t-Verteilung.

Diese Funktion ist die Umkehrfunktion der kumulativen Verteilungsfunktion (CDF) der Student-t-Verteilung und gibt t zurück, so dass stdtr(df, t) = p ist.

Gibt das Argument t zurück, so dass stdtr(df, t) gleich p ist.

Parameter:

dfarray_like

Freiheitsgrade

parray_like

Wahrscheinlichkeit

outndarray, optional

Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

tSkalar oder ndarray

Wert von t, so dass stdtr(df, t) == p

Siehe auch

stdtr

Student t CDF

stdtridf

Umkehrfunktion von stdtr in Bezug auf df

scipy.stats.t

Student-t-Verteilung

Hinweise

Die Student-t-Verteilung ist auch als scipy.stats.t verfügbar. Das direkte Aufrufen von stdtrit kann die Leistung im Vergleich zur ppf-Methode von scipy.stats.t verbessern (siehe letztes Beispiel unten).

stdtrit unterstützt neben NumPy experimentell auch Backends, die mit dem Python Array API Standard kompatibel sind. Bitte testen Sie diese Funktionen, indem Sie die Umgebungsvariable SCIPY_ARRAY_API=1 setzen und CuPy-, PyTorch-, JAX- oder Dask-Arrays als Array-Argumente übergeben. Die folgenden Kombinationen von Backend und Gerät (oder anderer Fähigkeit) werden unterstützt.

Bibliothek	CPU	GPU
NumPy	✅	n/a
CuPy	n/a	✅
PyTorch	✅	⛔
JAX	⛔	⛔
Dask	✅	n/a

Siehe Unterstützung für den Array API Standard für weitere Informationen.

Beispiele

Probieren Sie es in Ihrem Browser aus!

stdtrit repräsentiert die Umkehrfunktion der Student-t-Verteilung CDF, die als stdtr verfügbar ist. Hier berechnen wir die CDF für df bei x=1. stdtrit gibt dann 1 bis auf Fließkommafehler zurück, gegeben denselben Wert für df und den berechneten CDF-Wert.

>>> import numpy as np
>>> from scipy.special import stdtr, stdtrit
>>> import matplotlib.pyplot as plt
>>> df = 3
>>> x = 1
>>> cdf_value = stdtr(df, x)
>>> stdtrit(df, cdf_value)
0.9999999994418539

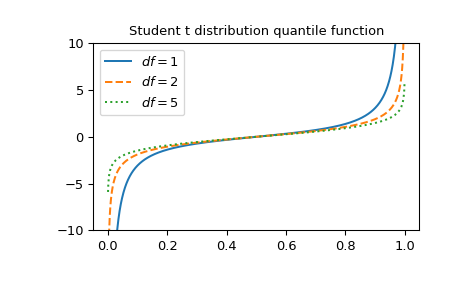
Stellen Sie die Funktion für drei verschiedene Freiheitsgrade dar.

>>> x = np.linspace(0, 1, 1000)
>>> parameters = [(1, "solid"), (2, "dashed"), (5, "dotted")]
>>> fig, ax = plt.subplots()
>>> for (df, linestyle) in parameters:
...     ax.plot(x, stdtrit(df, x), ls=linestyle, label=f"$df={df}$")
>>> ax.legend()
>>> ax.set_ylim(-10, 10)
>>> ax.set_title("Student t distribution quantile function")
>>> plt.show()

Die Funktion kann für mehrere Freiheitsgrade gleichzeitig berechnet werden, indem ein NumPy-Array oder eine Liste für df übergeben wird.

>>> stdtrit([1, 2, 3], 0.7)
array([0.72654253, 0.6172134 , 0.58438973])

Es ist möglich, die Funktion an mehreren Punkten für mehrere verschiedene Freiheitsgrade gleichzeitig zu berechnen, indem Arrays für df und p mit Formen, die für Broadcasting geeignet sind, übergeben werden. Berechnen Sie stdtrit an 4 Punkten für 3 Freiheitsgrade, was zu einem Array der Form 3x4 führt.

>>> dfs = np.array([[1], [2], [3]])
>>> p = np.array([0.2, 0.4, 0.7, 0.8])
>>> dfs.shape, p.shape
((3, 1), (4,))

>>> stdtrit(dfs, p)
array([[-1.37638192, -0.3249197 ,  0.72654253,  1.37638192],
       [-1.06066017, -0.28867513,  0.6172134 ,  1.06066017],
       [-0.97847231, -0.27667066,  0.58438973,  0.97847231]])

Die t-Verteilung ist auch als scipy.stats.t verfügbar. Das direkte Aufrufen von stdtrit kann wesentlich schneller sein als das Aufrufen der ppf-Methode von scipy.stats.t. Um dieselben Ergebnisse zu erhalten, muss die folgende Parametrisierung verwendet werden: scipy.stats.t(df).ppf(x) = stdtrit(df, x).

>>> from scipy.stats import t
>>> df, x = 3, 0.5
>>> stdtrit_result = stdtrit(df, x)  # this can be faster than below
>>> stats_result = t(df).ppf(x)
>>> stats_result == stdtrit_result  # test that results are equal
True

ZurückIn Tab öffnen