scipy.special.struve#

scipy.special.struve(v, x, out=None) = <ufunc 'struve'>#

Struve-Funktion.

Gibt den Wert der Struve-Funktion der Ordnung v bei x zurück. Die Struve-Funktion ist definiert als,

\[H_v(x) = (z/2)^{v + 1} \sum_{n=0}^\infty \frac{(-1)^n (z/2)^{2n}}{\Gamma(n + \frac{3}{2}) \Gamma(n + v + \frac{3}{2})},\]

wobei \(\Gamma\) die Gamma-Funktion ist.

Parameter:

varray_like: Ordnung der Struve-Funktion (Float).
xarray_like: Argument der Struve-Funktion (Float; muss positiv sein, es sei denn, v ist eine ganze Zahl).
outndarray, optional: Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

HSkalar oder ndarray: Wert der Struve-Funktion der Ordnung v bei x.

Siehe auch

modstruve: Modifizierte Struve-Funktion

Hinweise

Drei Methoden, die in [1] diskutiert werden, werden zur Auswertung der Struve-Funktion verwendet.

Potenzreihenentwicklung
Entwicklung in Bessel-Funktionen (wenn \(|z| < |v| + 20\))
asymptotische Groß-z-Entwicklung (wenn \(z \geq 0.7v + 12\))

Rundungsfehler werden basierend auf den größten Termen in den Summen geschätzt, und das Ergebnis mit dem kleinsten Fehler wird zurückgegeben.

Referenzen

[1]

NIST Digital Library of Mathematical Functions https://dlmf.nist.gov/11

Beispiele

Berechnen Sie die Struve-Funktion der Ordnung 1 bei 2.

>>> import numpy as np
>>> from scipy.special import struve
>>> import matplotlib.pyplot as plt
>>> struve(1, 2.)
0.6467637282835622

Berechnen Sie die Struve-Funktion bei 2 für die Ordnungen 1, 2 und 3, indem Sie eine Liste für den Ordnungs-Parameter v bereitstellen.

>>> struve([1, 2, 3], 2.)
array([0.64676373, 0.28031806, 0.08363767])

Berechnen Sie die Struve-Funktion der Ordnung 1 für mehrere Punkte, indem Sie ein Array für x bereitstellen.

>>> points = np.array([2., 5., 8.])
>>> struve(1, points)
array([0.64676373, 0.80781195, 0.48811605])

Berechnen Sie die Struve-Funktion für mehrere Ordnungen an mehreren Punkten, indem Sie Arrays für v und z bereitstellen. Die Arrays müssen zu den korrekten Formen broadcastbar sein.

>>> orders = np.array([[1], [2], [3]])
>>> points.shape, orders.shape
((3,), (3, 1))

>>> struve(orders, points)
array([[0.64676373, 0.80781195, 0.48811605],
       [0.28031806, 1.56937455, 1.51769363],
       [0.08363767, 1.50872065, 2.98697513]])

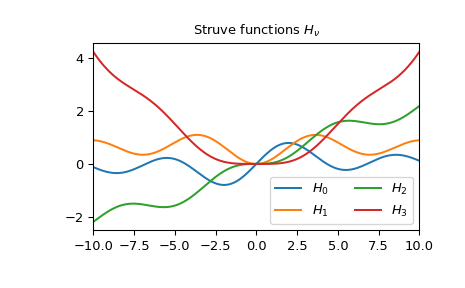
Plotten Sie die Struve-Funktionen der Ordnungen 0 bis 3 von -10 bis 10.

>>> fig, ax = plt.subplots()
>>> x = np.linspace(-10., 10., 1000)
>>> for i in range(4):
...     ax.plot(x, struve(i, x), label=f'$H_{i!r}$')
>>> ax.legend(ncol=2)
>>> ax.set_xlim(-10, 10)
>>> ax.set_title(r"Struve functions $H_{\nu}$")
>>> plt.show()

../../_images/scipy-special-struve-1.png