scipy.stats.

permutation_test#

scipy.stats.permutation_test(data, statistic, *, permutation_type='independent', vectorized=None, n_resamples=9999, batch=None, alternative='two-sided', axis=0, rng=None)[Quelle]#

Führt einen Permutationstest einer gegebenen Statistik auf bereitgestellten Daten durch.

Bei unabhängigen Stichprobenstatistiken ist die Nullhypothese, dass die Daten zufällig aus derselben Verteilung gezogen werden. Bei gepaarten Stichprobenstatistiken können zwei Nullhypothesen getestet werden: dass die Daten zufällig gepaart werden oder dass die Daten zufällig Stichproben zugewiesen werden.

Parameter:

dataIterable von Array-ähnlichen Objekten

Enthält die Stichproben, von denen jede ein Array von Beobachtungen ist. Die Dimensionen der Stichproben-Arrays müssen kompatibel für Broadcasting sein, außer entlang axis.

statisticaufrufbar

Statistik, für die der p-Wert des Hypothesentests berechnet werden soll. statistic muss eine aufrufbare Funktion sein, die Stichproben als separate Argumente akzeptiert (z. B. statistic(*data)) und die resultierende Statistik zurückgibt. Wenn vectorized auf True gesetzt ist, muss statistic auch ein Schlüsselwortargument axis akzeptieren und vektorisiert sein, um die Statistik entlang der bereitgestellten axis der Stichproben-Arrays zu berechnen.

permutation_type{‘independent’, ‘samples’, ‘pairings’}, optional

Der Typ der durchzuführenden Permutationen in Übereinstimmung mit der Nullhypothese. Die ersten beiden Permutationstypen sind für gepaarte Stichprobenstatistiken, bei denen alle Stichproben die gleiche Anzahl von Beobachtungen enthalten und Beobachtungen mit entsprechenden Indizes entlang axis als gepaart betrachtet werden; der dritte ist für unabhängige Stichprobenstatistiken.

'samples' : Beobachtungen werden verschiedenen Stichproben zugewiesen, bleiben aber mit denselben Beobachtungen aus anderen Stichproben gepaart. Dieser Permutationstyp ist geeignet für gepaarte Stichproben-Hypothesentests wie den Wilcoxon-Vorzeichen-Rang-Test und den gepaarten t-Test.
'pairings' : Beobachtungen werden mit verschiedenen Beobachtungen gepaart, bleiben aber innerhalb derselben Stichprobe. Dieser Permutationstyp ist geeignet für Assoziations-/Korrelationstests mit Statistiken wie Spearmans \(\rho\), Kendalls \(\tau\) und Pearsons \(r\).
'independent' (Standard) : Beobachtungen werden verschiedenen Stichproben zugewiesen. Stichproben können unterschiedliche Anzahlen von Beobachtungen enthalten. Dieser Permutationstyp ist geeignet für unabhängige Stichproben-Hypothesentests wie den Mann-Whitney \(U\)-Test und den unabhängigen Stichproben-t-Test.

Bitte lesen Sie den Abschnitt Hinweise unten für detailliertere Beschreibungen der Permutationstypen.

vectorizedbool, optional

Wenn vectorized auf False gesetzt ist, wird statistic nicht das Schlüsselwortargument axis übergeben und es wird erwartet, dass die Statistik nur für 1D-Stichproben berechnet wird. Wenn True, wird statistic das Schlüsselwortargument axis übergeben und es wird erwartet, dass die Statistik entlang axis berechnet wird, wenn ein ND-Stichproben-Array übergeben wird. Wenn None (Standard), wird vectorized auf True gesetzt, wenn axis ein Parameter von statistic ist. Die Verwendung einer vektorisierten Statistik reduziert typischerweise die Rechenzeit.

n_resamplesint oder np.inf, Standard: 9999

Anzahl der zufälligen Permutationen (Resamples), die zur Annäherung der Nullverteilung verwendet werden. Wenn sie größer oder gleich der Anzahl der verschiedenen Permutationen ist, wird die exakte Nullverteilung berechnet. Beachten Sie, dass die Anzahl der verschiedenen Permutationen mit der Größe der Stichproben sehr schnell anwächst, sodass exakte Tests nur für sehr kleine Datensätze praktikabel sind.

batchint, optional

Die Anzahl der Permutationen, die in jedem Aufruf von statistic verarbeitet werden. Der Speicherbedarf beträgt O( batch * n ), wobei n die Gesamtgröße aller Stichproben ist, unabhängig vom Wert von vectorized. Der Standardwert ist None, in diesem Fall ist batch die Anzahl der Permutationen.

alternative{‘zweiseitig’, ‘kleiner’, ‘größer’}, optional

Die alternative Hypothese, für die der p-Wert berechnet wird. Für jede Alternative wird der p-Wert bei exakten Tests wie folgt definiert.

'greater' : der Prozentsatz der Nullverteilung, der größer oder gleich dem beobachteten Wert der Teststatistik ist.
'less' : der Prozentsatz der Nullverteilung, der kleiner oder gleich dem beobachteten Wert der Teststatistik ist.
'two-sided' (Standard) : doppelt so klein wie die p-Werte oben.

Beachten Sie, dass p-Werte für randomisierte Tests gemäß der konservativen (überschätzten) Annäherung berechnet werden, wie in [2] und [3] vorgeschlagen, anstatt des unverzerrten Schätzers, wie in [4] vorgeschlagen. Das heißt, bei der Berechnung des Anteils der randomisierten Nullverteilung, der so extrem ist wie der beobachtete Wert der Teststatistik, werden die Werte im Zähler und Nenner beide um eins erhöht. Eine Interpretation dieser Anpassung ist, dass der beobachtete Wert der Teststatistik immer als Element der randomisierten Nullverteilung enthalten ist. Die Konvention für zweiseitige p-Werte ist nicht universell; die beobachtete Teststatistik und die Nullverteilung werden zurückgegeben, falls eine andere Definition bevorzugt wird.

axisint, Standard: 0

Die Achse der (broadcasteten) Stichproben, über die die Statistik berechnet werden soll. Wenn Stichproben eine unterschiedliche Anzahl von Dimensionen haben, werden Einzeldimensionen vor axis zu Stichproben mit weniger Dimensionen hinzugefügt.

rng{None, int, numpy.random.Generator}, optional

Wenn rng als Schlüsselwort übergeben wird, werden andere Typen als numpy.random.Generator an numpy.random.default_rng übergeben, um einen Generator zu instanziieren. Wenn rng bereits eine Generator-Instanz ist, dann wird die bereitgestellte Instanz verwendet. Geben Sie rng für reproduzierbares Funktionsverhalten an.

Wenn dieses Argument positional übergeben wird oder random_state als Schlüsselwort übergeben wird, gilt das ältere Verhalten für das Argument random_state.

Wenn random_state None ist (oder numpy.random), wird die Singleton-Instanz numpy.random.RandomState verwendet.
Wenn random_state eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit random_state initialisiert wurde.
Wenn random_state bereits eine Generator- oder RandomState-Instanz ist, wird diese Instanz verwendet.

Geändert in Version 1.15.0: Im Rahmen der SPEC-007-Umstellung von der Verwendung von numpy.random.RandomState auf numpy.random.Generator wurde dieses Schlüsselwort von random_state zu rng geändert. Für eine Übergangszeit werden beide Schlüsselwörter weiterhin funktionieren, obwohl nur eines gleichzeitig angegeben werden kann. Nach der Übergangszeit werden Funktionsaufrufe mit dem Schlüsselwort random_state Warnungen ausgeben. Das Verhalten von sowohl random_state als auch rng ist oben beschrieben, aber nur das Schlüsselwort rng sollte in neuem Code verwendet werden.

Rückgabe:

resPermutationTestResult

Ein Objekt mit den Attributen

statisticfloat oder ndarray: Die beobachtete Teststatistik der Daten.
pvaluefloat oder ndarray: Der p-Wert für die gegebene Alternative.
null_distributionndarray: Die Werte der Teststatistik, die unter der Nullhypothese generiert wurden.

Hinweise

Die drei von dieser Funktion unterstützten Arten von Permutationstests sind unten beschrieben.

Ungepaarte Statistiken (permutation_type='independent')

Die Nullhypothese, die mit diesem Permutationstyp verbunden ist, besagt, dass alle Beobachtungen aus derselben zugrundeliegenden Verteilung gezogen werden und dass sie zufällig einer der Stichproben zugewiesen wurden.

Angenommen, data enthält zwei Stichproben; z. B. a, b = data. Wenn 1 < n_resamples < binom(n, k), wobei

k die Anzahl der Beobachtungen in a ist,
n die Gesamtzahl der Beobachtungen in a und b ist und
binom(n, k) der Binomialkoeffizient ist ( n über k ),

werden die Daten gepoolt (konkateniert), zufällig entweder der ersten oder der zweiten Stichprobe zugewiesen und die Statistik berechnet. Dieser Vorgang wird wiederholt, permutation Mal, wodurch eine Verteilung der Statistik unter der Nullhypothese erzeugt wird. Die Statistik der ursprünglichen Daten wird mit dieser Verteilung verglichen, um den p-Wert zu ermitteln.

Wenn n_resamples >= binom(n, k), wird ein exakter Test durchgeführt: Die Daten werden in jeder unterschiedlichen Weise zwischen den Stichproben partitioniert und die exakte Nullverteilung gebildet. Beachten Sie, dass für eine gegebene Partitionierung der Daten zwischen den Stichproben nur eine Reihenfolge/Permutation der Daten innerhalb jeder Stichprobe berücksichtigt wird. Für Statistiken, die nicht von der Reihenfolge der Daten innerhalb der Stichproben abhängen, reduziert dies die Rechenkosten drastisch, ohne die Form der Nullverteilung zu beeinflussen (da die Häufigkeit/Anzahl jedes Wertes durch denselben Faktor beeinflusst wird).

Für a = [a1, a2, a3, a4] und b = [b1, b2, b3] ist ein Beispiel für diesen Permutationstyp x = [b3, a1, a2, b2] und y = [a4, b1, a3]. Da bei einem exakten Test nur eine Reihenfolge/Permutation der Daten innerhalb jeder Stichprobe berücksichtigt wird, wäre eine Resample wie x = [b3, a1, b2, a2] und y = [a4, a3, b1] nicht als vom obigen Beispiel unterscheidbar betrachtet.

permutation_type='independent' unterstützt keine Ein-Stichproben-Statistiken, kann aber auf Statistiken mit mehr als zwei Stichproben angewendet werden. In diesem Fall ist, wenn n ein Array der Anzahl der Beobachtungen innerhalb jeder Stichprobe ist, die Anzahl der unterschiedlichen Partitionen

np.prod([binom(sum(n[i:]), sum(n[i+1:])) for i in range(len(n)-1)])

Gepaarte Statistiken, Permutation von Paaren (permutation_type='pairings')

Die Nullhypothese, die mit diesem Permutationstyp verbunden ist, besagt, dass Beobachtungen innerhalb jedes Paares aus derselben zugrundeliegenden Verteilung stammen und dass die Paarungen mit Elementen anderer Stichproben zufällig zugewiesen werden.

Angenommen, data enthält nur eine Stichprobe; z. B. a, = data, und wir möchten alle möglichen Paarungen von Elementen von a mit Elementen einer zweiten Stichprobe, b, betrachten. Sei n die Anzahl der Beobachtungen in a, die auch der Anzahl der Beobachtungen in b entsprechen muss.

Wenn 1 < n_resamples < factorial(n), werden die Elemente von a zufällig permutiert. Die vom Benutzer bereitgestellte Statistik akzeptiert ein Datenargument, z. B. a_perm, und berechnet die Statistik unter Berücksichtigung von a_perm und b. Dieser Vorgang wird wiederholt, permutation Mal, wodurch eine Verteilung der Statistik unter der Nullhypothese erzeugt wird. Die Statistik der ursprünglichen Daten wird mit dieser Verteilung verglichen, um den p-Wert zu ermitteln.

Wenn n_resamples >= factorial(n), wird ein exakter Test durchgeführt: a wird in jeder unterschiedlichen Weise genau einmal permutiert. Daher wird die statistic für jede eindeutige Paarung von Stichproben zwischen a und b genau einmal berechnet.

Für a = [a1, a2, a3] und b = [b1, b2, b3] ist ein Beispiel für diesen Permutationstyp a_perm = [a3, a1, a2], während b in seiner ursprünglichen Reihenfolge bleibt.

permutation_type='pairings' unterstützt data, das eine beliebige Anzahl von Stichproben enthält, von denen jede die gleiche Anzahl von Beobachtungen enthalten muss. Alle in data bereitgestellten Stichproben werden unabhängig permutiert. Daher ist, wenn m die Anzahl der Stichproben und n die Anzahl der Beobachtungen innerhalb jeder Stichprobe ist, die Anzahl der Permutationen bei einem exakten Test

factorial(n)**m

Beachten Sie, dass, wenn eine zweiseitige Statistik beispielsweise nicht inhärent von der Reihenfolge abhängt, in der Beobachtungen bereitgestellt werden - nur von den Paarungen von Beobachtungen -, dann nur eine der beiden Stichproben in data bereitgestellt werden sollte. Dies reduziert die Rechenkosten drastisch, ohne die Form der Nullverteilung zu beeinflussen (da die Häufigkeit/Anzahl jedes Wertes durch denselben Faktor beeinflusst wird).

Gepaarte Statistiken, Permutation von Stichproben (permutation_type='samples')

Die Nullhypothese, die mit diesem Permutationstyp verbunden ist, besagt, dass Beobachtungen innerhalb jedes Paares aus derselben zugrundeliegenden Verteilung stammen und dass die Stichprobe, der sie zugewiesen werden, zufällig ist.

Angenommen, data enthält zwei Stichproben; z. B. a, b = data. Sei n die Anzahl der Beobachtungen in a, die auch der Anzahl der Beobachtungen in b entsprechen muss.

Wenn 1 < n_resamples < 2**n, werden die Elemente von a und b zufällig zwischen Stichproben vertauscht (wobei ihre Paarungen beibehalten werden) und die Statistik wird berechnet. Dieser Vorgang wird wiederholt, permutation Mal, wodurch eine Verteilung der Statistik unter der Nullhypothese erzeugt wird. Die Statistik der ursprünglichen Daten wird mit dieser Verteilung verglichen, um den p-Wert zu ermitteln.

Wenn n_resamples >= 2**n, wird ein exakter Test durchgeführt: Die Beobachtungen werden jeder Stichprobe in jeder unterschiedlichen Weise (wobei Paarungen beibehalten werden) genau einmal zugewiesen.

Für a = [a1, a2, a3] und b = [b1, b2, b3] ist ein Beispiel für diesen Permutationstyp x = [b1, a2, b3] und y = [a1, b2, a3].

permutation_type='samples' unterstützt data, das eine beliebige Anzahl von Stichproben enthält, von denen jede die gleiche Anzahl von Beobachtungen enthalten muss. Wenn data mehr als eine Stichprobe enthält, werden gepaarte Beobachtungen innerhalb von data unabhängig zwischen den Stichproben ausgetauscht. Daher ist, wenn m die Anzahl der Stichproben und n die Anzahl der Beobachtungen innerhalb jeder Stichprobe ist, die Anzahl der Permutationen bei einem exakten Test

factorial(m)**n

Mehrere gepaarte Stichproben-Statistiken, wie der Wilcoxon-Vorzeichen-Rang-Test und der gepaarte Stichproben-t-Test, können unter Berücksichtigung nur der Differenz zwischen zwei gepaarten Elementen durchgeführt werden. Dementsprechend wird, wenn data nur eine Stichprobe enthält, die Nullverteilung gebildet, indem unabhängig das Vorzeichen jeder Beobachtung geändert wird.

Warnung

Der p-Wert wird berechnet, indem die Elemente der Nullverteilung gezählt werden, die so extrem oder extremer als der beobachtete Wert der Statistik sind. Aufgrund der Verwendung von endlicher Präzisionsarithmetik geben einige Statistikfunktionen numerisch unterschiedliche Werte zurück, wenn die theoretischen Werte exakt gleich wären. In einigen Fällen könnte dies zu einem großen Fehler im berechneten p-Wert führen. permutation_test schützt davor, indem Elemente in der Nullverteilung, die "nah" (innerhalb einer relativen Toleranz von 100 mal dem Fließkomma-Epsilon von ungenauen DTypes) am beobachteten Wert der Teststatistik liegen, als gleich dem beobachteten Wert der Teststatistik betrachtet werden. Es wird jedoch dem Benutzer geraten, die Nullverteilung zu überprüfen, um zu beurteilen, ob diese Vergleichsmethode geeignet ist, und falls nicht, den p-Wert manuell zu berechnen. Siehe Beispiel unten.

Referenzen

[1]

1. Fisher. The Design of Experiments, 6th Ed (1951).

[2]

B. Phipson und G. K. Smyth. „Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.“ Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

[3]

M. D. Ernst. „Permutation Methods: A Basis for Exact Inference“. Statistical Science (2004).

[4]

B. Efron und R. J. Tibshirani. An Introduction to the Bootstrap (1993).

Beispiele

Nehmen wir an, wir möchten testen, ob zwei Stichproben aus derselben Verteilung gezogen wurden. Angenommen, die zugrundeliegenden Verteilungen sind uns unbekannt, und dass wir vor der Beobachtung der Daten die Hypothese aufgestellt haben, dass der Mittelwert der ersten Stichprobe kleiner als der der zweiten Stichprobe sein würde. Wir beschließen, die Differenz zwischen den Stichprobenmittelwerten als Teststatistik zu verwenden, und wir werden einen p-Wert von 0,05 als statistisch signifikant betrachten.

Aus Effizienzgründen schreiben wir die Funktion, die die Teststatistik definiert, in vektorisierter Form: Die Stichproben x und y können ND-Arrays sein, und die Statistik wird für jede Achsenscheibe entlang von axis berechnet.

>>> import numpy as np
>>> def statistic(x, y, axis):
...     return np.mean(x, axis=axis) - np.mean(y, axis=axis)

Nachdem wir unsere Daten gesammelt haben, berechnen wir den beobachteten Wert der Teststatistik.

>>> from scipy.stats import norm
>>> rng = np.random.default_rng()
>>> x = norm.rvs(size=5, random_state=rng)
>>> y = norm.rvs(size=6, loc = 3, random_state=rng)
>>> statistic(x, y, 0)
-3.5411688580987266

Tatsächlich ist die Teststatistik negativ, was darauf hindeutet, dass der wahre Mittelwert der zugrundeliegenden Verteilung von x kleiner ist als der der zugrundeliegenden Verteilung von y. Um die Wahrscheinlichkeit zu ermitteln, dass dies zufällig geschieht, wenn die beiden Stichproben aus derselben Verteilung gezogen wurden, führen wir einen Permutationstest durch.

>>> from scipy.stats import permutation_test
>>> # because our statistic is vectorized, we pass `vectorized=True`
>>> # `n_resamples=np.inf` indicates that an exact test is to be performed
>>> res = permutation_test((x, y), statistic, vectorized=True,
...                        n_resamples=np.inf, alternative='less')
>>> print(res.statistic)
-3.5411688580987266
>>> print(res.pvalue)
0.004329004329004329

Die Wahrscheinlichkeit, unter der Nullhypothese eine Teststatistik zu erhalten, die kleiner oder gleich dem beobachteten Wert ist, beträgt 0,4329 %. Dies ist kleiner als unser gewählter Schwellenwert von 5 %, daher betrachten wir dies als signifikanten Beweis gegen die Nullhypothese zugunsten der Alternative.

Da die Größe der obigen Stichproben klein war, konnte permutation_test einen exakten Test durchführen. Für größere Stichproben greifen wir auf einen randomisierten Permutationstest zurück.

>>> x = norm.rvs(size=100, random_state=rng)
>>> y = norm.rvs(size=120, loc=0.2, random_state=rng)
>>> res = permutation_test((x, y), statistic, n_resamples=9999,
...                        vectorized=True, alternative='less',
...                        rng=rng)
>>> print(res.statistic)
-0.4230459671240913
>>> print(res.pvalue)
0.0015

Die ungefähre Wahrscheinlichkeit, unter der Nullhypothese eine Teststatistik zu erhalten, die kleiner oder gleich dem beobachteten Wert ist, beträgt 0,0225 %. Dies ist wiederum kleiner als unser gewählter Schwellenwert von 5 %, daher haben wir erneut signifikante Beweise, um die Nullhypothese zugunsten der Alternative zu verwerfen.

Bei großen Stichproben und einer großen Anzahl von Permutationen ist das Ergebnis vergleichbar mit dem des entsprechenden asymptotischen Tests, dem unabhängigen Stichproben-t-Test.

>>> from scipy.stats import ttest_ind
>>> res_asymptotic = ttest_ind(x, y, alternative='less')
>>> print(res_asymptotic.pvalue)
0.0014669545224902675

Die Permutationsverteilung der Teststatistik wird zur weiteren Untersuchung bereitgestellt.

>>> import matplotlib.pyplot as plt
>>> plt.hist(res.null_distribution, bins=50)
>>> plt.title("Permutation distribution of test statistic")
>>> plt.xlabel("Value of Statistic")
>>> plt.ylabel("Frequency")
>>> plt.show()

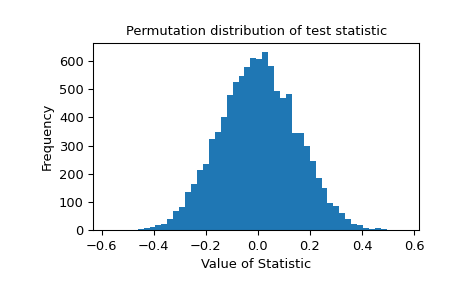
../../_images/scipy-stats-permutation_test-1_00_00.png

Die Überprüfung der Nullverteilung ist unerlässlich, wenn die Statistik aufgrund begrenzter Maschinenpräzision ungenau ist. Betrachten Sie den folgenden Fall

>>> from scipy.stats import pearsonr
>>> x = [1, 2, 4, 3]
>>> y = [2, 4, 6, 8]
>>> def statistic(x, y, axis=-1):
...     return pearsonr(x, y, axis=axis).statistic
>>> res = permutation_test((x, y), statistic, vectorized=True,
...                        permutation_type='pairings',
...                        alternative='greater')
>>> r, pvalue, null = res.statistic, res.pvalue, res.null_distribution

In diesem Fall unterscheiden sich einige Elemente der Nullverteilung aufgrund von numerischem Rauschen vom beobachteten Wert des Korrelationskoeffizienten r. Wir überprüfen manuell die Elemente der Nullverteilung, die nahezu gleich dem beobachteten Wert der Teststatistik sind.

>>> r
0.7999999999999999
>>> unique = np.unique(null)
>>> unique
array([-1. , -1. , -0.8, -0.8, -0.8, -0.6, -0.4, -0.4, -0.2, -0.2, -0.2,
    0. ,  0.2,  0.2,  0.2,  0.4,  0.4,  0.6,  0.8,  0.8,  0.8,  1. ,
    1. ])  # may vary
>>> unique[np.isclose(r, unique)].tolist()
[0.7999999999999998, 0.7999999999999999, 0.8]  # may vary

Wenn permutation_test den Vergleich naiv durchführen würde, würden die Elemente der Nullverteilung mit dem Wert 0.7999999999999998 nicht als extrem oder extremer als der beobachtete Wert der Statistik betrachtet werden, sodass der berechnete p-Wert zu klein wäre.

>>> incorrect_pvalue = np.count_nonzero(null >= r) / len(null)
>>> incorrect_pvalue
0.14583333333333334  # may vary

Stattdessen behandelt permutation_test Elemente der Nullverteilung, die innerhalb von max(1e-14, abs(r)*1e-14) vom beobachteten Wert der Statistik r liegen, als gleich r.

>>> correct_pvalue = np.count_nonzero(null >= r - 1e-14) / len(null)
>>> correct_pvalue
0.16666666666666666
>>> res.pvalue == correct_pvalue
True

Diese Vergleichsmethode wird voraussichtlich in den meisten praktischen Situationen genau sein, aber dem Benutzer wird geraten, dies zu bewerten, indem die Elemente der Nullverteilung überprüft werden, die nahe am beobachteten Wert der Statistik liegen. Erwägen Sie auch die Verwendung von Statistiken, die mit exakter Arithmetik berechnet werden können (z. B. ganzzahlige Statistiken).