bootstrap#
- scipy.stats.bootstrap(data, statistic, *, n_resamples=9999, batch=None, vectorized=None, paired=False, axis=0, confidence_level=0.95, alternative='two-sided', method='BCa', bootstrap_result=None, rng=None)[Quelle]#
Berechnet ein zweiseitiges Bootstrap-Konfidenzintervall für eine Statistik.
Wenn method
'percentile'und alternative'two-sided'ist, wird ein Bootstrap-Konfidenzintervall nach folgendem Verfahren berechnet.Resampling der Daten: Für jede Stichprobe in data und für jede der n_resamples Wiederholungen wird eine zufällige Stichprobe aus der ursprünglichen Stichprobe (mit Zurücklegen) mit der gleichen Größe wie die ursprüngliche Stichprobe gezogen.
Berechnung der Bootstrap-Verteilung der Statistik: Für jeden Satz von Resamples wird die Teststatistik berechnet.
Bestimmung des Konfidenzintervalls: Ermittlung des Intervalls der Bootstrap-Verteilung, das
symmetrisch um den Median ist und
zu confidence_level der resampelten Statistikwerte enthält.
Während die Methode
'percentile'am intuitivsten ist, wird sie in der Praxis selten verwendet. Zwei gebräuchlichere Methoden sind'basic'(„reverse percentile“) und'BCa'(„bias-corrected and accelerated“); sie unterscheiden sich darin, wie Schritt 3 durchgeführt wird.Wenn die Stichproben in data zufällig aus ihren jeweiligen Verteilungen \(n\) Mal gezogen werden, enthält das von
bootstrapzurückgegebene Konfidenzintervall den wahren Wert der Statistik für diese Verteilungen ungefähr confidence_level\(\, \times \, n\) Mal.- Parameter:
- dataSequenz von array-ähnlichen Objekten
Jedes Element von data ist eine Stichprobe, die skalare Beobachtungen aus einer zugrunde liegenden Verteilung enthält. Die Elemente von data müssen broadcast-fähig sein, um die gleiche Form zu haben (mit der möglichen Ausnahme der durch axis angegebenen Dimension).
- statisticaufrufbar
Statistik, für die das Konfidenzintervall berechnet werden soll. statistic muss eine aufrufbare Funktion sein, die
len(data)Stichproben als separate Argumente akzeptiert und die resultierende Statistik zurückgibt. Wenn vectorized aufTruegesetzt ist, muss statistic auch ein Schlüsselwortargument axis akzeptieren und vektorisiert sein, um die Statistik entlang der angegebenen axis zu berechnen.- n_resamplesint, Standard:
9999 Die Anzahl der durchgeführten Resamples zur Bildung der Bootstrap-Verteilung der Statistik.
- batchint, optional
Die Anzahl der Resamples, die in jedem vektorisierten Aufruf von statistic verarbeitet werden. Der Speicherverbrauch beträgt O( batch *
n), wobeindie Stichprobengröße ist. Standard istNone, in diesem Fall istbatch = n_resamples(oderbatch = max(n_resamples, n)fürmethod='BCa').- vectorizedbool, optional
Wenn vectorized auf
Falsegesetzt ist, wird statistic nicht das Schlüsselwortargument axis übergeben und es wird erwartet, dass die Statistik nur für 1D-Stichproben berechnet wird. WennTrue, wird statistic das Schlüsselwortargument axis übergeben und es wird erwartet, dass die Statistik entlang axis berechnet wird, wenn ein ND-Stichprobenarray übergeben wird. WennNone(Standard), wird vectorized aufTruegesetzt, wennaxisein Parameter von statistic ist. Die Verwendung einer vektorisierten Statistik reduziert typischerweise die Berechnungszeit.- pairedbool, Standard:
False Ob die Statistik entsprechende Elemente der Stichproben in data als gepaart behandelt. Wenn True, resampelt
bootstrapein Array von *Indizes* und verwendet dieselben Indizes für alle Arrays in data; andernfalls resampeltbootstrapunabhängig die Elemente jedes Arrays.- axisint, Standard:
0 Die Achse der Stichproben in data, entlang der die statistic berechnet wird.
- confidence_levelfloat, Standard:
0.95 Das Konfidenzniveau des Konfidenzintervalls.
- alternative{‘two-sided’, ‘less’, ‘greater’}, Standard:
'two-sided' Wählen Sie
'two-sided'(Standard) für ein zweiseitiges Konfidenzintervall,'less'für ein einseitiges Konfidenzintervall mit der unteren Grenze bei-np.infund'greater'für ein einseitiges Konfidenzintervall mit der oberen Grenze beinp.inf. Die andere Grenze der einseitigen Konfidenzintervalle ist dieselbe wie die eines zweiseitigen Konfidenzintervalls mit confidence_level, das doppelt so weit von 1.0 entfernt ist; z.B. ist die obere Grenze eines 95%'less'Konfidenzintervalls dieselbe wie die obere Grenze eines 90%'two-sided'Konfidenzintervalls.- method{‘percentile’, ‘basic’, ‘bca’}, Standard:
'BCa' Ob das Bootstrap-Konfidenzintervall vom Typ „percentile“ (
'percentile'), „basic“ (auch „reverse“) ('basic') oder das bias-korrigierte und beschleunigte Bootstrap-Konfidenzintervall ('BCa') zurückgegeben werden soll.- bootstrap_resultBootstrapResult, optional
Stellen Sie das Ergebnisobjekt zur Verfügung, das von einem vorherigen Aufruf von
bootstrapzurückgegeben wurde, um die vorherige Bootstrap-Verteilung in die neue Bootstrap-Verteilung einzubeziehen. Dies kann beispielsweise verwendet werden, um confidence_level oder method zu ändern oder um die Auswirkung zusätzlicher Resampling-Vorgänge zu sehen, ohne Berechnungen zu wiederholen.- rng{None, int,
numpy.random.Generator}, optional Wenn rng als Schlüsselwort übergeben wird, werden andere Typen als
numpy.random.Generatorannumpy.random.default_rngübergeben, um einenGeneratorzu instanziieren. Wenn rng bereits eineGenerator-Instanz ist, dann wird die bereitgestellte Instanz verwendet. Geben Sie rng für reproduzierbares Funktionsverhalten an.Wenn dieses Argument positional übergeben wird oder random_state als Schlüsselwort übergeben wird, gilt das ältere Verhalten für das Argument random_state.
Wenn random_state None ist (oder
numpy.random), wird die Singleton-Instanznumpy.random.RandomStateverwendet.Wenn random_state eine Ganzzahl ist, wird eine neue
RandomState-Instanz verwendet, die mit random_state initialisiert wurde.Wenn random_state bereits eine
Generator- oderRandomState-Instanz ist, wird diese Instanz verwendet.
Geändert in Version 1.15.0: Als Teil des SPEC-007-Übergangs von der Verwendung von
numpy.random.RandomStatezunumpy.random.Generatorwurde dieses Schlüsselwort von random_state in rng geändert. Für eine Übergangszeit werden beide Schlüsselwörter weiterhin funktionieren, obwohl nur eines gleichzeitig angegeben werden kann. Nach der Übergangszeit geben Funktionsaufrufe, die das Schlüsselwort random_state verwenden, Warnungen aus. Das Verhalten von sowohl random_state als auch rng wird oben beschrieben, aber nur das Schlüsselwort rng sollte in neuem Code verwendet werden.
- Rückgabe:
- resBootstrapResult
Ein Objekt mit den Attributen
- confidence_intervalConfidenceInterval
Das Bootstrap-Konfidenzintervall als Instanz von
collections.namedtuplemit den Attributen low und high.- bootstrap_distributionndarray
Die Bootstrap-Verteilung, d.h. der Wert von statistic für jeden Resample. Die letzte Dimension entspricht den Resamples (z.B.
res.bootstrap_distribution.shape[-1] == n_resamples).- standard_errorfloat oder ndarray
Der Bootstrap-Standardfehler, d.h. die Stichprobenstandardabweichung der Bootstrap-Verteilung.
- Warnungen:
DegenerateDataWarningWird generiert, wenn
method='BCa'und die Bootstrap-Verteilung degeneriert ist (z.B. alle Elemente sind identisch).
Hinweise
Elemente des Konfidenzintervalls können für
method='BCa'NaN sein, wenn die Bootstrap-Verteilung degeneriert ist (z.B. alle Elemente sind identisch). In diesem Fall sollten Sie eine andere method verwenden oder data auf Hinweise untersuchen, dass andere Analysen geeigneter sein könnten (z.B. alle Beobachtungen sind identisch).Referenzen
[1]B. Efron und R. J. Tibshirani, An Introduction to the Bootstrap, Chapman & Hall/CRC, Boca Raton, FL, USA (1993)
[2]Nathaniel E. Helwig, „Bootstrap Confidence Intervals“, http://users.stat.umn.edu/~helwig/notes/bootci-Notes.pdf
[3]Bootstrapping (Statistik), Wikipedia, https://en.wikipedia.org/wiki/Bootstrapping_%28statistics%29
Beispiele
Angenommen, wir haben Daten aus einer unbekannten Verteilung gezogen.
>>> import numpy as np >>> rng = np.random.default_rng() >>> from scipy.stats import norm >>> dist = norm(loc=2, scale=4) # our "unknown" distribution >>> data = dist.rvs(size=100, random_state=rng)
Wir sind an der Standardabweichung der Verteilung interessiert.
>>> std_true = dist.std() # the true value of the statistic >>> print(std_true) 4.0 >>> std_sample = np.std(data) # the sample statistic >>> print(std_sample) 3.9460644295563863
Das Bootstrap-Verfahren wird verwendet, um die Variabilität zu approximieren, die wir erwarten würden, wenn wir wiederholt aus der unbekannten Verteilung ziehen und jedes Mal die Statistik der Stichprobe berechnen würden. Dies geschieht durch wiederholtes Resampling von Werten *aus der ursprünglichen Stichprobe* mit Zurücklegen und Berechnung der Statistik jedes Resamples. Dies ergibt eine „Bootstrap-Verteilung“ der Statistik.
>>> import matplotlib.pyplot as plt >>> from scipy.stats import bootstrap >>> data = (data,) # samples must be in a sequence >>> res = bootstrap(data, np.std, confidence_level=0.9, rng=rng) >>> fig, ax = plt.subplots() >>> ax.hist(res.bootstrap_distribution, bins=25) >>> ax.set_title('Bootstrap Distribution') >>> ax.set_xlabel('statistic value') >>> ax.set_ylabel('frequency') >>> plt.show()
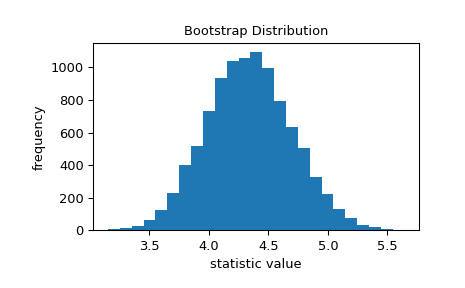
Der Standardfehler quantifiziert diese Variabilität. Er wird als die Standardabweichung der Bootstrap-Verteilung berechnet.
>>> res.standard_error 0.24427002125829136 >>> res.standard_error == np.std(res.bootstrap_distribution, ddof=1) True
Die Bootstrap-Verteilung der Statistik ist oft annähernd normal mit einer Skala, die dem Standardfehler entspricht.
>>> x = np.linspace(3, 5) >>> pdf = norm.pdf(x, loc=std_sample, scale=res.standard_error) >>> fig, ax = plt.subplots() >>> ax.hist(res.bootstrap_distribution, bins=25, density=True) >>> ax.plot(x, pdf) >>> ax.set_title('Normal Approximation of the Bootstrap Distribution') >>> ax.set_xlabel('statistic value') >>> ax.set_ylabel('pdf') >>> plt.show()
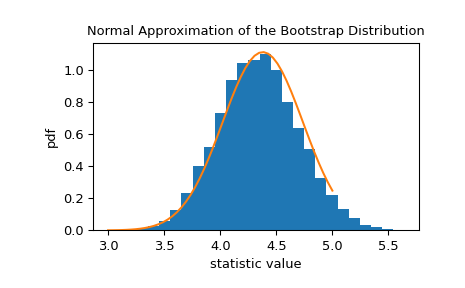
Dies legt nahe, dass wir ein 90%iges Konfidenzintervall für die Statistik basierend auf den Quantilen dieser Normalverteilung konstruieren könnten.
>>> norm.interval(0.9, loc=std_sample, scale=res.standard_error) (3.5442759991341726, 4.3478528599786)
Aufgrund des zentralen Grenzwertsatzes ist diese Normalapproximation für eine Vielzahl von Statistiken und zugrunde liegenden Verteilungen der Stichproben genau; die Approximation ist jedoch nicht in allen Fällen zuverlässig. Da
bootstrapso konzipiert ist, dass es mit beliebigen zugrunde liegenden Verteilungen und Statistiken funktioniert, verwendet es fortschrittlichere Techniken, um ein genaues Konfidenzintervall zu generieren.>>> print(res.confidence_interval) ConfidenceInterval(low=3.57655333533867, high=4.382043696342881)
Wenn wir 100 Mal aus der ursprünglichen Verteilung ziehen und für jede Stichprobe ein Bootstrap-Konfidenzintervall bilden, enthält das Konfidenzintervall den wahren Wert der Statistik etwa 90% der Zeit.
>>> n_trials = 100 >>> ci_contains_true_std = 0 >>> for i in range(n_trials): ... data = (dist.rvs(size=100, random_state=rng),) ... res = bootstrap(data, np.std, confidence_level=0.9, ... n_resamples=999, rng=rng) ... ci = res.confidence_interval ... if ci[0] < std_true < ci[1]: ... ci_contains_true_std += 1 >>> print(ci_contains_true_std) 88
Anstatt eine Schleife zu schreiben, können wir auch die Konfidenzintervalle für alle 100 Stichproben auf einmal ermitteln.
>>> data = (dist.rvs(size=(n_trials, 100), random_state=rng),) >>> res = bootstrap(data, np.std, axis=-1, confidence_level=0.9, ... n_resamples=999, rng=rng) >>> ci_l, ci_u = res.confidence_interval
Hier enthalten ci_l und ci_u das Konfidenzintervall für jede der
n_trials = 100Stichproben.>>> print(ci_l[:5]) [3.86401283 3.33304394 3.52474647 3.54160981 3.80569252] >>> print(ci_u[:5]) [4.80217409 4.18143252 4.39734707 4.37549713 4.72843584]
Und wieder enthalten etwa 90% den wahren Wert,
std_true = 4.>>> print(np.sum((ci_l < std_true) & (std_true < ci_u))) 93
bootstrapkann auch verwendet werden, um Konfidenzintervalle für mehrfache Stichprobenstatistiken zu schätzen. Um beispielsweise ein Konfidenzintervall für die Differenz zweier Mittelwerte zu erhalten, schreiben wir eine Funktion, die zwei Stichprobenargumente akzeptiert und nur die Statistik zurückgibt. Die Verwendung des Argumentsaxisstellt sicher, dass alle Mittelwertberechnungen in einem einzigen vektorisierten Aufruf erfolgen, was schneller ist, als über Paare von Resamples in Python zu iterieren.>>> def my_statistic(sample1, sample2, axis=-1): ... mean1 = np.mean(sample1, axis=axis) ... mean2 = np.mean(sample2, axis=axis) ... return mean1 - mean2
Hier verwenden wir die Methode 'percentile' mit dem Standard-Konfidenzniveau von 95%.
>>> sample1 = norm.rvs(scale=1, size=100, random_state=rng) >>> sample2 = norm.rvs(scale=2, size=100, random_state=rng) >>> data = (sample1, sample2) >>> res = bootstrap(data, my_statistic, method='basic', rng=rng) >>> print(my_statistic(sample1, sample2)) 0.16661030792089523 >>> print(res.confidence_interval) ConfidenceInterval(low=-0.29087973240818693, high=0.6371338699912273)
Der Bootstrap-Schätzer für den Standardfehler ist ebenfalls verfügbar.
>>> print(res.standard_error) 0.238323948262459
Gepaarte Stichprobenstatistiken funktionieren ebenfalls. Betrachten wir zum Beispiel den Pearson-Korrelationskoeffizienten.
>>> from scipy.stats import pearsonr >>> n = 100 >>> x = np.linspace(0, 10, n) >>> y = x + rng.uniform(size=n) >>> print(pearsonr(x, y)[0]) # element 0 is the statistic 0.9954306665125647
Wir wickeln
pearsonrso ein, dass es nur die Statistik zurückgibt, und stellen sicher, dass wir das Argument axis verwenden, da es verfügbar ist.>>> def my_statistic(x, y, axis=-1): ... return pearsonr(x, y, axis=axis)[0]
Wir rufen
bootstrapmitpaired=Trueauf.>>> res = bootstrap((x, y), my_statistic, paired=True, rng=rng) >>> print(res.confidence_interval) ConfidenceInterval(low=0.9941504301315878, high=0.996377412215445)
Das Ergebnisobjekt kann an
bootstrapzurückgegeben werden, um zusätzliche Resampling-Vorgänge durchzuführen>>> len(res.bootstrap_distribution) 9999 >>> res = bootstrap((x, y), my_statistic, paired=True, ... n_resamples=1000, rng=rng, ... bootstrap_result=res) >>> len(res.bootstrap_distribution) 10999
oder um die Optionen für das Konfidenzintervall zu ändern
>>> res2 = bootstrap((x, y), my_statistic, paired=True, ... n_resamples=0, rng=rng, bootstrap_result=res, ... method='percentile', confidence_level=0.9) >>> np.testing.assert_equal(res2.bootstrap_distribution, ... res.bootstrap_distribution) >>> res.confidence_interval ConfidenceInterval(low=0.9941574828235082, high=0.9963781698210212)
ohne die Berechnung der ursprünglichen Bootstrap-Verteilung zu wiederholen.