scipy.stats.sampling.

DiscreteGuideTable#

class scipy.stats.sampling.DiscreteGuideTable(dist, *, domain=None, guide_factor=1, random_state=None)#

Methode der diskreten Führungstabelle.

Die Methode der diskreten Führungstabelle generiert Stichproben aus beliebigen, aber endlichen Wahrscheinlichkeitsvektoren. Sie verwendet den Wahrscheinlichkeitsvektor der Größe \(N\) oder eine Wahrscheinlichkeitsmassenfunktion mit endlichem Träger, um Zufallszahlen aus der Verteilung zu erzeugen. Die diskrete Führungstabelle hat eine sehr langsame Einrichtung (linear mit der Vektorlänge), bietet aber eine sehr schnelle Stichprobenerzeugung.

Parameter:

distarray_like oder Objekt, optional

Wahrscheinlichkeitsvektor (PV) der Verteilung. Wenn kein PV verfügbar ist, wird eine Instanz einer Klasse mit einer pmf Methode erwartet. Die Signatur der PMF wird wie folgt erwartet: def pmf(self, k: int) -> float. D.h. sie sollte einen Python-Integer akzeptieren und einen Python-Float zurückgeben.

domainint, optional

Träger der PMF. Wenn kein Wahrscheinlichkeitsvektor (pv) verfügbar ist, muss ein endlicher Träger angegeben werden. D.h. die PMF muss einen endlichen Träger haben. Standard ist None. Wenn None

Wenn eine support-Methode vom Verteilungsobjekt dist bereitgestellt wird, wird sie verwendet, um den Definitionsbereich der Verteilung festzulegen.
Andernfalls wird angenommen, dass der Träger (0, len(pv)) ist. Wenn dieser Parameter in Kombination mit einem Wahrscheinlichkeitsvektor übergeben wird, wird domain[0] verwendet, um die Verteilung von (0, len(pv)) auf (domain[0], domain[0]+len(pv)) zu verschieben, und domain[1] wird ignoriert. Siehe Hinweise und Tutorial für eine detailliertere Erklärung.

guide_factor: int, optional

Größe der Führungstabelle relativ zur Länge des PV. Größere Führungstabellen führen zu schnelleren Generierungszeiten, erfordern aber eine teurere Einrichtung. Größen größer als 3 werden nicht empfohlen. Wenn die relative Größe auf 0 gesetzt wird, wird die sequentielle Suche verwendet. Standard ist 1.

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState}, optional

Ein NumPy-Zufallszahlengenerator oder ein Seed für den zugrundeliegenden NumPy-Zufallszahlengenerator, der zum Generieren des Stroms von gleichmäßigen Zufallszahlen verwendet wird. Wenn random_state None ist (oder np.random), wird die Singleton-Instanz numpy.random.RandomState verwendet. Wenn random_state eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit random_state initialisiert wird. Wenn random_state bereits eine Generator- oder RandomState-Instanz ist, dann wird diese Instanz verwendet.

Methoden

`ppf`(u)	PPF der gegebenen Verteilung.
`rvs`([size, random_state])	Stichprobe aus der Verteilung.
`set_random_state`([random_state])	Setzt den zugrunde liegenden gleichmäßigen Zufallszahlengenerator.

Hinweise

Diese Methode funktioniert, wenn entweder ein endlicher Wahrscheinlichkeitsvektor verfügbar ist oder die PMF der Verteilung verfügbar ist. Wenn nur eine PMF verfügbar ist, muss auch der *endliche* Träger (domain) der PMF angegeben werden. Es wird empfohlen, zuerst den Wahrscheinlichkeitsvektor zu erhalten, indem die PMF an jedem Punkt des Trägers ausgewertet wird, und diesen dann stattdessen zu verwenden.

DGT generiert Stichproben aus beliebigen, aber endlichen Wahrscheinlichkeitsvektoren. Zufallszahlen werden durch die Inversionsmethode generiert, d.h.

Generieren Sie eine Zufallszahl U ~ U(0,1).
Finden Sie die kleinste ganze Zahl I, so dass F(I) = P(X<=I) >= U.

Schritt (2) ist der entscheidende Schritt. Die sequentielle Suche erfordert O(E(X)) Vergleiche, wobei E(X) der Erwartungswert der Verteilung ist. Die indizierte Suche verwendet jedoch eine Führungstabelle, um zu einem I' <= I nahe I zu springen, um X in konstanter Zeit zu finden. Tatsächlich wird die erwartete Anzahl von Vergleichen auf 2 reduziert, wenn die Führungstabelle die gleiche Größe wie der Wahrscheinlichkeitsvektor hat (dies ist der Standard). Für größere Führungstabellen wird diese Zahl kleiner (ist aber immer größer als 1), für kleinere Tabellen wird sie größer. Für den Grenzfall der Tabellengröße 1 führt der Algorithmus einfach eine sequentielle Suche durch.

Andererseits beträgt die Einrichtungszeit für die Führungstabelle O(N), wobei N die Länge des Wahrscheinlichkeitsvektors bezeichnet (für Größe 1 ist keine Vorverarbeitung erforderlich). Darüber hinaus können bei sehr großen Führungstabellen Speichereffekte die Geschwindigkeit des Algorithmus sogar verringern. Daher empfehlen wir keine Führungstabellen, die mehr als dreimal so groß sind wie der gegebene Wahrscheinlichkeitsvektor. Wenn nur wenige Zufallszahlen generiert werden müssen, sind (viel) kleinere Tabellengrößen besser. Die Größe der Führungstabelle relativ zur Länge des gegebenen Wahrscheinlichkeitsvektors kann über den Parameter guide_factor eingestellt werden.

Wenn ein Wahrscheinlichkeitsvektor angegeben wird, muss er ein eindimensionales Array aus nicht-negativen Gleitkommazahlen ohne inf oder nan Werte sein. Außerdem muss es mindestens einen Nicht-Null-Eintrag geben, sonst wird eine Ausnahme ausgelöst.

Standardmäßig wird der Wahrscheinlichkeitsvektor ab 0 indiziert. Dies kann jedoch durch Angabe eines domain-Parameters geändert werden. Wenn domain in Kombination mit dem PV angegeben wird, hat dies den Effekt, die Verteilung von (0, len(pv)) auf (domain[0], domain[0] + len(pv)) zu verschieben. domain[1] wird in diesem Fall ignoriert.

Referenzen

[1]

UNU.RAN Referenzhandbuch, Abschnitt 5.8.4, „DGT - (Discrete) Guide Table method (indexed search)“ https://statmath.wu.ac.at/unuran/doc/unuran.html#DGT

[2]

H.C. Chen und Y. Asau (1974). On generating random variates from an empirical distribution, AIIE Trans. 6, S. 163-166.

Beispiele

>>> from scipy.stats.sampling import DiscreteGuideTable
>>> import numpy as np

Um einen Zufallszahlengenerator mit einem Wahrscheinlichkeitsvektor zu erstellen, verwenden Sie

>>> pv = [0.1, 0.3, 0.6]
>>> urng = np.random.default_rng()
>>> rng = DiscreteGuideTable(pv, random_state=urng)

Der RNG wurde eingerichtet. Nun können wir die Methode rvs verwenden, um Stichproben aus der Verteilung zu generieren

>>> rvs = rng.rvs(size=1000)

Um zu überprüfen, ob die Zufallsvariaten der gegebenen Verteilung folgen, können wir den Chi-Quadrat-Test verwenden (als Maß für die Anpassungsgüte)

>>> from scipy.stats import chisquare
>>> _, freqs = np.unique(rvs, return_counts=True)
>>> freqs = freqs / np.sum(freqs)
>>> freqs
array([0.092, 0.355, 0.553])
>>> chisquare(freqs, pv).pvalue
0.9987382966178464

Da der p-Wert sehr hoch ist, lehnen wir die Nullhypothese, dass die beobachteten Häufigkeiten mit den erwarteten Häufigkeiten übereinstimmen, nicht ab. Daher können wir sicher davon ausgehen, dass die Zufallsvariaten aus der gegebenen Verteilung generiert wurden. Beachten Sie, dass dies nur die Korrektheit des Algorithmus und nicht die Qualität der Stichproben angibt.

Wenn kein PV verfügbar ist, kann auch eine Instanz einer Klasse mit einer PMF-Methode und einem endlichen Träger übergeben werden.

>>> urng = np.random.default_rng()
>>> from scipy.stats import binom
>>> n, p = 10, 0.2
>>> dist = binom(n, p)
>>> rng = DiscreteGuideTable(dist, random_state=urng)

Nun können wir aus der Verteilung über die Methode rvs Stichproben ziehen und auch die Anpassungsgüte der Stichproben messen

>>> rvs = rng.rvs(1000)
>>> _, freqs = np.unique(rvs, return_counts=True)
>>> freqs = freqs / np.sum(freqs)
>>> obs_freqs = np.zeros(11)  # some frequencies may be zero.
>>> obs_freqs[:freqs.size] = freqs
>>> pv = [dist.pmf(i) for i in range(0, 11)]
>>> pv = np.asarray(pv) / np.sum(pv)
>>> chisquare(obs_freqs, pv).pvalue
0.9999999999999989

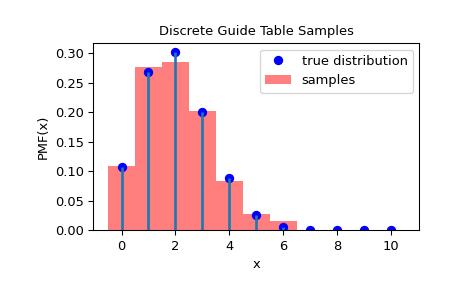
Um zu überprüfen, ob die Stichproben aus der richtigen Verteilung gezogen wurden, können wir das Histogramm der Stichproben visualisieren

>>> import matplotlib.pyplot as plt
>>> rvs = rng.rvs(1000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> x = np.arange(0, n+1)
>>> fx = dist.pmf(x)
>>> fx = fx / fx.sum()
>>> ax.plot(x, fx, 'bo', label='true distribution')
>>> ax.vlines(x, 0, fx, lw=2)
>>> ax.hist(rvs, bins=np.r_[x, n+1]-0.5, density=True, alpha=0.5,
...         color='r', label='samples')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PMF(x)')
>>> ax.set_title('Discrete Guide Table Samples')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-stats-sampling-DiscreteGuideTable-1_00_00.png

Um die Größe der Führungstabelle festzulegen, verwenden Sie das Schlüsselwortargument guide_factor. Dies legt die Größe der Führungstabelle relativ zum Wahrscheinlichkeitsvektor fest

>>> rng = DiscreteGuideTable(pv, guide_factor=1, random_state=urng)

Um die PPF einer Binomialverteilung mit \(n=4\) und \(p=0.1\) zu berechnen: Wir können wie folgt eine Führungstabelle einrichten

>>> n, p = 4, 0.1
>>> dist = binom(n, p)
>>> rng = DiscreteGuideTable(dist, random_state=42)
>>> rng.ppf(0.5)
0.0