NumericalInversePolynomial#
- class scipy.stats.sampling.NumericalInversePolynomial(dist, *, mode=None, center=None, domain=None, order=5, u_resolution=1e-10, random_state=None)#
Polynomial-Interpolation basierte INVerse der CDF (PINV).
PINV ist eine Variante der numerischen Invertierung, bei der die inverse CDF mittels Newtons Interpolationsformel angenähert wird. Das Intervall
[0,1]wird in mehrere Teilintervalle unterteilt. In jedem dieser Teilintervalle wird die inverse CDF an den Knotenpunkten(CDF(x),x)für einige Punktexin diesem Teilintervall konstruiert. Wenn die PDF gegeben ist, wird die CDF numerisch aus der gegebenen PDF mittels adaptiver Gauss-Lobatto-Integration mit 5 Punkten berechnet. Teilintervalle werden solange aufgeteilt, bis das geforderte Genauigkeitsziel erreicht ist.Die Methode ist nicht exakt, da sie nur Zufallsvariaten der approximierten Verteilung erzeugt. Dennoch kann der maximal tolerierte Approximationsfehler auf die Auflösung (aber natürlich begrenzt durch die Maschinenpräzision) gesetzt werden. Wir verwenden den u-Fehler
|U - CDF(X)|zur Fehlervermessung, wobeiXdas approximierte Perzentil ist, das dem QuantilUentspricht, d.h.X = approx_ppf(U). Wir nennen den maximal tolerierten u-Fehler die u-Auflösung des Algorithmus.Sowohl die Ordnung des interpolierenden Polynoms als auch die u-Auflösung können ausgewählt werden. Beachten Sie, dass sehr kleine Werte der u-Auflösung möglich sind, aber die Kosten für den Einrichtungsschritt erhöhen.
Die interpolierenden Polynome müssen in einem Einrichtungsschritt berechnet werden. Sie funktioniert jedoch nur für Verteilungen mit endlichem Definitionsbereich; für Verteilungen mit unendlichem Definitionsbereich werden die Enden abgeschnitten, so dass die Wahrscheinlichkeit für die Endbereiche im Vergleich zur gegebenen u-Auflösung gering ist.
Die Konstruktion des Interpolationspolynoms funktioniert nur, wenn die PDF unimodal ist oder wenn die PDF zwischen zwei Modi nicht verschwindet.
Es gibt einige Einschränkungen für die gegebene Verteilung
Die Unterstützung der Verteilung (d.h. der Bereich, in dem die PDF strikt positiv ist) muss zusammenhängend sein. In der Praxis bedeutet dies, dass der Bereich, in dem die PDF „nicht zu klein“ ist, zusammenhängend sein muss. Unimodale Dichten erfüllen diese Bedingung. Wenn diese Bedingung verletzt wird, kann der Definitionsbereich der Verteilung abgeschnitten werden.
Wenn die PDF numerisch integriert wird, muss die gegebene PDF kontinuierlich und glatt sein.
Die PDF muss beschränkt sein.
Der Algorithmus hat Probleme, wenn die Verteilung schwere Enden hat (da die inverse CDF bei 0 oder 1 sehr steil wird) und die angeforderte u-Auflösung sehr klein ist. Z.B. zeigt die Cauchy-Verteilung wahrscheinlich dieses Problem, wenn die angeforderte u-Auflösung kleiner als 1.e-12 ist.
- Parameter:
- distObjekt
Eine Instanz einer Klasse mit einer
pdf- oderlogpdf-Methode, optional einecdf-Methode.pdf: PDF der Verteilung. Die Signatur der PDF wird erwartet als:def pdf(self, x: float) -> float, d.h. die PDF sollte einen Python-Float akzeptieren und einen Python-Float zurückgeben. Sie muss sich nicht zu 1 integrieren, d.h. die PDF muss nicht normalisiert sein. Diese Methode ist optional, aber entwederpdfoderlogpdfmuss angegeben werden. Wenn beide gegeben sind, wirdlogpdfverwendet.logpdf: Der Logarithmus der PDF der Verteilung. Die Signatur ist dieselbe wie fürpdf. Ebenso kann der Logarithmus der Normalisierungskonstante der PDF ignoriert werden. Diese Methode ist optional, aber entwederpdfoderlogpdfmuss angegeben werden. Wenn beide gegeben sind, wirdlogpdfverwendet.cdf: CDF der Verteilung. Diese Methode ist optional. Wenn sie angegeben wird, ermöglicht sie die Berechnung des „u-Fehlers“. Sieheu_error. Muss dieselbe Signatur wie die PDF haben.
- modefloat, optional
(Exakter) Modus der Verteilung. Standard ist
None.- centerfloat, optional
Ungefähre Lage des Modus oder des Mittelwerts der Verteilung. Diese Lage liefert Informationen über den Hauptteil der PDF und wird verwendet, um numerische Probleme zu vermeiden. Standard ist
None.- domainListe oder Tupel der Länge 2, optional
Die Unterstützung der Verteilung. Standard ist
None. WennNoneWenn eine
support-Methode vom Verteilungsobjekt dist bereitgestellt wird, wird sie verwendet, um den Definitionsbereich der Verteilung festzulegen.Andernfalls wird die Unterstützung als \((-\infty, \infty)\) angenommen.
- orderint, optional
Ordnung des interpolierenden Polynoms. Gültige Ordnungen liegen zwischen 3 und 17. Höhere Ordnungen führen zu weniger Intervallen für die Annäherungen. Standard ist 5.
- u_resolutionfloat, optional
Setzt den maximal tolerierten u-Fehler. Werte von u_resolution müssen mindestens 1.e-15 und höchstens 1.e-5 betragen. Beachten Sie, dass die Auflösung der meisten gleichmäßigen Zufallszahlengeneratoren 2-32 = 2.3e-10 beträgt. Ein Wert von 1.e-10 führt also zu einem Invertierungsalgorithmus, der als exakt bezeichnet werden könnte. Für die meisten Simulationen sind auch etwas größere Werte für den maximalen Fehler ausreichend. Standard ist 1e-10.
- random_state{None, int,
numpy.random.Generator, numpy.random.RandomState}, optionalEin NumPy-Zufallszahlengenerator oder ein Seed für den zugrunde liegenden NumPy-Zufallszahlengenerator, der zum Erzeugen des Stroms von gleichmäßigen Zufallszahlen verwendet wird. Wenn random_state None ist (oder np.random), wird die Singleton-Instanz
numpy.random.RandomStateverwendet. Wenn random_state ein int ist, wird eine neueRandomState-Instanz mit random_state als Seed verwendet. Wenn random_state bereits eineGenerator- oderRandomState-Instanz ist, wird diese Instanz verwendet.
- Attribute:
intervalsGibt die Anzahl der im Berechnungsprozess verwendeten Intervalle zurück.
Methoden
cdf(x)Approximierte kumulative Verteilungsfunktion der gegebenen Verteilung.
ppf(u)Approximierte PPF (Prozentrangfunktion) der gegebenen Verteilung.
qrvs([size, d, qmc_engine])Quasi-Zufallsvariaten der gegebenen RV.
rvs([size, random_state])Stichprobe aus der Verteilung.
set_random_state([random_state])Setzt den zugrunde liegenden gleichmäßigen Zufallszahlengenerator.
u_error([sample_size])Schätzt den u-Fehler der Approximation mittels Monte-Carlo-Simulation.
Referenzen
[1]Derflinger, Gerhard, Wolfgang Hörmann, und Josef Leydold. „Random variate generation by numerical inversion when only the density is known.“ ACM Transactions on Modeling and Computer Simulation (TOMACS) 20.4 (2010): 1-25.
[2]UNU.RAN Referenzhandbuch, Abschnitt 5.3.12, „PINV - Polynomial interpolation based INVersion of CDF“, https://statmath.wu.ac.at/software/unuran/doc/unuran.html#PINV
Beispiele
>>> from scipy.stats.sampling import NumericalInversePolynomial >>> from scipy.stats import norm >>> import numpy as np
Um einen Generator zur Stichprobenentnahme aus der Standardnormalverteilung zu erstellen, tun Sie Folgendes:
>>> class StandardNormal: ... def pdf(self, x): ... return np.exp(-0.5 * x*x) ... >>> dist = StandardNormal() >>> urng = np.random.default_rng() >>> rng = NumericalInversePolynomial(dist, random_state=urng)
Nachdem ein Generator erstellt wurde, können Stichproben aus der Verteilung gezogen werden, indem die Methode
rvsaufgerufen wird.>>> rng.rvs() -1.5244996276336318
Um zu überprüfen, ob die Zufallsvariaten der gegebenen Verteilung genau folgen, können wir uns ihr Histogramm ansehen.
>>> import matplotlib.pyplot as plt >>> rvs = rng.rvs(10000) >>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000) >>> fx = norm.pdf(x) >>> plt.plot(x, fx, 'r-', lw=2, label='true distribution') >>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates') >>> plt.xlabel('x') >>> plt.ylabel('PDF(x)') >>> plt.title('Numerical Inverse Polynomial Samples') >>> plt.legend() >>> plt.show()

Es ist möglich, den u-Fehler der approximierten PPF zu schätzen, wenn die exakte CDF während der Einrichtung verfügbar ist. Um dies zu tun, übergeben Sie ein dist-Objekt mit der exakten CDF der Verteilung während der Initialisierung.
>>> from scipy.special import ndtr >>> class StandardNormal: ... def pdf(self, x): ... return np.exp(-0.5 * x*x) ... def cdf(self, x): ... return ndtr(x) ... >>> dist = StandardNormal() >>> urng = np.random.default_rng() >>> rng = NumericalInversePolynomial(dist, random_state=urng)
Nun kann der u-Fehler durch Aufrufen der Methode
u_errorgeschätzt werden. Sie führt eine Monte-Carlo-Simulation durch, um den u-Fehler zu schätzen. Standardmäßig werden 100000 Stichproben verwendet. Um dies zu ändern, können Sie die Anzahl der Stichproben als Argument übergeben.>>> rng.u_error(sample_size=1000000) # uses one million samples UError(max_error=8.785994154436594e-11, mean_absolute_error=2.930890027826552e-11)
Dies gibt ein benanntes Tupel zurück, das den maximalen u-Fehler und den mittleren absoluten u-Fehler enthält.
Der u-Fehler kann durch Verringern der u-Auflösung (maximal zulässiger u-Fehler) reduziert werden.
>>> urng = np.random.default_rng() >>> rng = NumericalInversePolynomial(dist, u_resolution=1.e-12, random_state=urng) >>> rng.u_error(sample_size=1000000) UError(max_error=9.07496300328603e-13, mean_absolute_error=3.5255644517257716e-13)
Beachten Sie, dass dies auf Kosten einer erhöhten Einrichtungszeit geht.
Die approximierte PPF kann durch Aufrufen der Methode
ppfausgewertet werden.>>> rng.ppf(0.975) 1.9599639857012559 >>> norm.ppf(0.975) 1.959963984540054
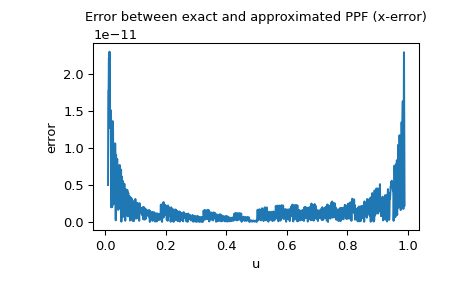
Da die PPF der Normalverteilung als spezielle Funktion verfügbar ist, können wir auch den x-Fehler überprüfen, d.h. die Differenz zwischen der approximierten PPF und der exakten PPF.
>>> import matplotlib.pyplot as plt >>> u = np.linspace(0.01, 0.99, 1000) >>> approxppf = rng.ppf(u) >>> exactppf = norm.ppf(u) >>> error = np.abs(exactppf - approxppf) >>> plt.plot(u, error) >>> plt.xlabel('u') >>> plt.ylabel('error') >>> plt.title('Error between exact and approximated PPF (x-error)') >>> plt.show()