scipy.stats.sampling.

TransformedDensityRejection#

class scipy.stats.sampling.TransformedDensityRejection(dist, *, mode=None, center=None, domain=None, c=-0.5, construction_points=30, use_dars=True, max_squeeze_hat_ratio=0.99, random_state=None)#

Transformed Density Rejection (TDR) Methode.

TDR ist eine Akzeptanz-/Verwerfungsmethode, die die Konkavität einer transformierten Dichte nutzt, um eine Hutfunktion zu konstruieren und diese automatisch zu "quetschen". Die meisten universellen Algorithmen sind sehr langsam im Vergleich zu Algorithmen, die auf eine spezifische Verteilung zugeschnitten sind. Algorithmen, die schnell sind, haben eine langsame Einrichtung und erfordern große Tabellen. Das Ziel dieser universellen Methode ist es, einen Algorithmus bereitzustellen, der nicht zu langsam ist und nur eine kurze Einrichtung benötigt. Diese Methode kann auf univariate und unimodale kontinuierliche Verteilungen mit T-konkaver Dichtefunktion angewendet werden. Weitere Details finden Sie unter [1] und [2].

Parameter:

distObjekt

Eine Instanz einer Klasse mit Methoden pdf und dpdf.

pdf: PDF der Verteilung. Die Signatur der PDF wird erwartet wie folgt: def pdf(self, x: float) -> float. Das heißt, die PDF sollte einen Python-Float akzeptieren und einen Python-Float zurückgeben. Sie muss nicht zu 1 integrieren, d. h. die PDF muss nicht normalisiert sein.
dpdf: Ableitung der PDF nach x (d. h. der Zufallsvariable). Muss dieselbe Signatur wie die PDF haben.

modefloat, optional

(Exakter) Modus der Verteilung. Standard ist None.

centerfloat, optional

Ungefähre Position des Modus oder des Mittelwerts der Verteilung. Diese Position liefert einige Informationen über den Hauptteil der PDF und wird verwendet, um numerische Probleme zu vermeiden. Standard ist None.

domainListe oder Tupel der Länge 2, optional

Die Unterstützung der Verteilung. Standard ist None. Wenn None

Wenn eine support-Methode vom Verteilungsobjekt dist bereitgestellt wird, wird sie verwendet, um den Definitionsbereich der Verteilung festzulegen.
Andernfalls wird die Unterstützung als \((-\infty, \infty)\) angenommen.

c{-0.5, 0.}, optional

Setzt den Parameter c für die Transformationsfunktion T. Der Standardwert ist -0.5. Die Transformation der PDF muss konkav sein, um die Hutfunktion konstruieren zu können. Eine solche PDF wird als T-konkav bezeichnet. Derzeit werden die folgenden Transformationen unterstützt:

\[\begin{split}c = 0.: T(x) &= \log(x)\\ c = -0.5: T(x) &= \frac{1}{\sqrt{x}} \text{ (Standard)}\end{split}\]

construction_pointsint oder array_like, optional

Wenn es sich um eine Ganzzahl handelt, definiert sie die Anzahl der Konstruktionspunkte. Wenn es sich um ein Array handelt, werden die Elemente des Arrays als Konstruktionspunkte verwendet. Standard ist 30.

use_darsbool, optional

Wenn True, wird "derandomized adaptive rejection sampling" (DARS) bei der Einrichtung verwendet. Siehe [1] für Details zum DARS-Algorithmus. Standard ist True.

max_squeeze_hat_ratiofloat, optional

Setzt die Obergrenze für das Verhältnis (Fläche unter der "Squeeze") / (Fläche unter dem "Hat"). Muss eine Zahl zwischen 0 und 1 sein. Standard ist 0.99.

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState}, optional

Ein NumPy-Zufallszahlengenerator oder ein Seed für den zugrunde liegenden NumPy-Zufallszahlengenerator, der zum Generieren des Stroms von gleichmäßigen Zufallszahlen verwendet wird. Wenn random_state None ist (oder np.random), wird die numpy.random.RandomState-Singleton verwendet. Wenn random_state eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit random_state initialisiert wird. Wenn random_state bereits eine Generator- oder RandomState-Instanz ist, dann wird diese Instanz verwendet.

Attribute:

hat_area: Ruft die Fläche unter dem Hut für den Generator ab.
squeeze_area: Ruft die Fläche unter der "Squeeze" für den Generator ab.
squeeze_hat_ratio: Ruft das aktuelle Verhältnis (Fläche unter der "Squeeze") / (Fläche unter dem "Hat") für den Generator ab.

Methoden

`ppf_hat`(u)	Evaluieren Sie die Umkehrfunktion der kumulativen Verteilungsfunktion (CDF) der Hutverteilung an der Stelle u.
`rvs`([size, random_state])	Stichprobe aus der Verteilung.
`set_random_state`([random_state])	Setzt den zugrunde liegenden gleichmäßigen Zufallszahlengenerator.

Referenzen

[1] (1,2)

UNU.RAN-Referenzhandbuch, Abschnitt 5.3.16, „TDR - Transformed Density Rejection“, http://statmath.wu.ac.at/software/unuran/doc/unuran.html#TDR

[2]

Hörmann, Wolfgang. “A rejection technique for sampling from T-concave distributions.” ACM Transactions on Mathematical Software (TOMS) 21.2 (1995): 182-193

[3]

W.R. Gilks und P. Wild (1992). Adaptive rejection sampling for Gibbs sampling, Applied Statistics 41, S. 337-348.

Beispiele

>>> from scipy.stats.sampling import TransformedDensityRejection
>>> import numpy as np

Angenommen, wir haben eine Dichte

\[\begin{split}f(x) = \begin{cases} 1 - x^2, & -1 \leq x \leq 1 \\ 0, & \text{sonst} \end{cases}\end{split}\]

Die Ableitung dieser Dichtefunktion ist

\[\begin{split}\frac{df(x)}{dx} = \begin{cases} -2x, & -1 \leq x \leq 1 \\ 0, & \text{sonst} \end{cases}\end{split}\]

Beachten Sie, dass die PDF nicht zu 1 integriert. Da es sich um eine verwerfungsbasierte Methode handelt, muss die PDF nicht normalisiert sein. Um den Generator zu initialisieren, können wir verwenden

>>> urng = np.random.default_rng()
>>> class MyDist:
...     def pdf(self, x):
...         return 1-x*x
...     def dpdf(self, x):
...         return -2*x
...
>>> dist = MyDist()
>>> rng = TransformedDensityRejection(dist, domain=(-1, 1),
...                                   random_state=urng)

Die Domäne kann sehr nützlich sein, um die Verteilung zu trunkieren, aber um sie nicht jedes Mal an den Konstruktor übergeben zu müssen, kann eine Standarddomäne durch Bereitstellung einer support-Methode im Verteilungsobjekt (dist) festgelegt werden.

>>> class MyDist:
...     def pdf(self, x):
...         return 1-x*x
...     def dpdf(self, x):
...         return -2*x
...     def support(self):
...         return (-1, 1)
...
>>> dist = MyDist()
>>> rng = TransformedDensityRejection(dist, random_state=urng)

Nun können wir die Methode rvs verwenden, um Stichproben aus der Verteilung zu generieren.

>>> rvs = rng.rvs(1000)

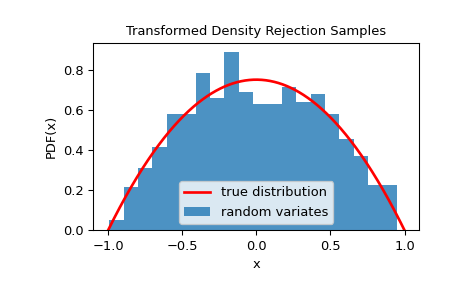
Wir können überprüfen, ob die Stichproben aus der gegebenen Verteilung stammen, indem wir ihr Histogramm visualisieren.

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-1, 1, 1000)
>>> fx = 3/4 * dist.pdf(x)  # 3/4 is the normalizing constant
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Transformed Density Rejection Samples')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-stats-sampling-TransformedDensityRejection-1.png