scipy.stats.studentized_range

scipy.stats.studentized_range = <scipy.stats._continuous_distns.studentized_range_gen Objekt>

Eine stochastische Variable mit stufenweiser Reichweite (studentized range).

Als Instanz der Klasse rv_continuous erbt das Objekt studentized_range von dieser eine Sammlung generischer Methoden (siehe unten für die vollständige Liste) und ergänzt diese mit Details, die spezifisch für diese Verteilung sind.

Methoden

rvs(k, df, loc=0, scale=1, size=1, random_state=None)	Zufallsvariaten.
pdf(x, k, df, loc=0, scale=1)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, k, df, loc=0, scale=1)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
cdf(x, k, df, loc=0, scale=1)	Kumulative Verteilungsfunktion.
logcdf(x, k, df, loc=0, scale=1)	Logarithmus der kumulativen Verteilungsfunktion.
sf(x, k, df, loc=0, scale=1)	Überlebensfunktion (auch definiert als 1 - cdf, aber sf ist manchmal genauer).
logsf(x, k, df, loc=0, scale=1)	Logarithmus der Überlebensfunktion.
ppf(q, k, df, loc=0, scale=1)	Perzentilpunktfunktion (Umkehrung von cdf — Perzentile).
isf(q, k, df, loc=0, scale=1)	Umgekehrte Überlebensfunktion (Umkehrung von sf).
moment(order, k, df, loc=0, scale=1)	Nichtzentrales Moment der angegebenen Ordnung.
stats(k, df, loc=0, scale=1, moments=’mv’)	Mittelwert(‚m‘), Varianz(‚v‘), Schiefe(‚s‘) und/oder Kurtosis(‚k‘).
entropy(k, df, loc=0, scale=1)	(Differential-)Entropie der RV.
fit(data)	Parameterschätzungen für generische Daten. Siehe scipy.stats.rv_continuous.fit für eine detaillierte Dokumentation der Schlüsselwortargumente.
expect(func, args=(k, df), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	Erwartungswert einer Funktion (einer Variablen) bezüglich der Verteilung.
median(k, df, loc=0, scale=1)	Median der Verteilung.
mean(k, df, loc=0, scale=1)	Mittelwert der Verteilung.
var(k, df, loc=0, scale=1)	Varianz der Verteilung.
std(k, df, loc=0, scale=1)	Standardabweichung der Verteilung.
interval(confidence, k, df, loc=0, scale=1)	Konfidenzintervall mit gleichen Flächen um den Median.

Siehe auch

t

Student's t-Verteilung

Hinweise

Die Wahrscheinlichkeitsdichtefunktion für studentized_range ist

\[f(x; k, \nu) = \frac{k(k-1)\nu^{\nu/2}}{\Gamma(\nu/2) 2^{\nu/2-1}} \int_{0}^{\infty} \int_{-\infty}^{\infty} s^{\nu} e^{-\nu s^2/2} \phi(z) \phi(sx + z) [\Phi(sx + z) - \Phi(z)]^{k-2} \,dz \,ds\]

für \(x ≥ 0\), \(k > 1\) und \(\nu > 0\).

studentized_range verwendet k für \(k\) und df für \(\nu\) als Formparameter.

Wenn \(\nu\) 100.000 überschreitet, wird eine asymptotische Näherung (unendliche Freiheitsgrade) verwendet, um die kumulative Verteilungsfunktion [4] und die Wahrscheinlichkeitsverteilungsfunktion zu berechnen.

Die obige Wahrscheinlichkeitsdichte ist in "standardisierter" Form definiert. Verwenden Sie die Parameter loc und scale, um die Verteilung zu verschieben und/oder zu skalieren. Genauer gesagt ist studentized_range.pdf(x, k, df, loc, scale) identisch mit studentized_range.pdf(y, k, df) / scale mit y = (x - loc) / scale. Beachten Sie, dass das Verschieben des Ortes einer Verteilung keine "nicht-zentrale" Verteilung daraus macht; nicht-zentrale Verallgemeinerungen einiger Verteilungen sind in separaten Klassen verfügbar.

Referenzen

[1]

„Studentized range distribution“, https://en.wikipedia.org/wiki/Studentized_range_distribution

[2]

Batista, Ben Dêivide, et al. „Externally Studentized Normal Midrange Distribution.“ Ciência e Agrotecnologia, vol. 41, no. 4, 2017, pp. 378-389., doi:10.1590/1413-70542017414047716.

[3]

Harter, H. Leon. „Tables of Range and Studentized Range.“ The Annals of Mathematical Statistics, vol. 31, no. 4, 1960, pp. 1122-1147. JSTOR, www.jstor.org/stable/2237810. Zugriff am 18. Februar 2021.

[4]

Lund, R. E. und J. R. Lund. „Algorithm AS 190: Probabilities and Upper Quantiles for the Studentized Range.“ Journal of the Royal Statistical Society. Series C (Applied Statistics), vol. 32, no. 2, 1983, pp. 204-210. JSTOR, www.jstor.org/stable/2347300. Zugriff am 18. Februar 2021.

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy.stats import studentized_range
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

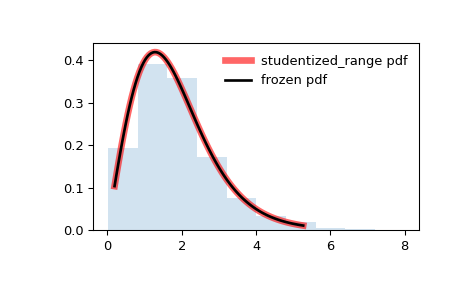
Zeigen Sie die Wahrscheinlichkeitsdichtefunktion (pdf) an

>>> k, df = 3, 10
>>> x = np.linspace(studentized_range.ppf(0.01, k, df),
...                 studentized_range.ppf(0.99, k, df), 100)
>>> ax.plot(x, studentized_range.pdf(x, k, df),
...         'r-', lw=5, alpha=0.6, label='studentized_range pdf')

Alternativ kann das Verteilungsobjekt (als Funktion) aufgerufen werden, um die Form-, Orts- und Skalierungsparameter festzulegen. Dies gibt ein „eingefrorenes“ RV-Objekt zurück, das die angegebenen Parameter beibehält.

Frieren Sie die Verteilung ein und zeigen Sie die eingefrorene pdf an

>>> rv = studentized_range(k, df)
>>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')

Überprüfen Sie die Genauigkeit von cdf und ppf

>>> vals = studentized_range.ppf([0.001, 0.5, 0.999], k, df)
>>> np.allclose([0.001, 0.5, 0.999], studentized_range.cdf(vals, k, df))
True

Anstatt (studentized_range.rvs) zum Erzeugen von Zufallsvariaten zu verwenden, was für diese Verteilung sehr langsam ist, können wir die inverse CDF mithilfe eines Interpolators annähern und dann Inverse-Transform-Sampling mit dieser approximierten inversen CDF durchführen.

Diese Verteilung hat einen unendlichen, aber dünnen rechten Schwanz, daher konzentrieren wir unsere Aufmerksamkeit auf die äußersten 99,9 Prozent.

>>> a, b = studentized_range.ppf([0, .999], k, df)
>>> a, b
0, 7.41058083802274

>>> from scipy.interpolate import interp1d
>>> rng = np.random.default_rng()
>>> xs = np.linspace(a, b, 50)
>>> cdf = studentized_range.cdf(xs, k, df)
# Create an interpolant of the inverse CDF
>>> ppf = interp1d(cdf, xs, fill_value='extrapolate')
# Perform inverse transform sampling using the interpolant
>>> r = ppf(rng.uniform(size=1000))

Und vergleichen Sie das Histogramm

>>> ax.hist(r, density=True, histtype='stepfilled', alpha=0.2)
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

ZurückIn Tab öffnen