Räumliche Datenstrukturen und Algorithmen (scipy.spatial)#
scipy.spatial kann Triangulierungen, Voronoi-Diagramme und konvexe Hüllen einer Punktmenge berechnen, indem es die Qhull-Bibliothek nutzt.
Darüber hinaus enthält es KDTree-Implementierungen für die Abfrage nächster Nachbarn und Dienstprogramme zur Entfernungsberechnung in verschiedenen Metriken.
Delaunay-Triangulierungen#
Die Delaunay-Triangulation ist eine Unterteilung einer Menge von Punkten in eine nicht überlappende Menge von Dreiecken, sodass kein Punkt innerhalb des Umkreises eines Dreiecks liegt. In der Praxis vermeiden solche Triangulierungen Dreiecke mit kleinen Winkeln.
Die Delaunay-Triangulation kann mit scipy.spatial wie folgt berechnet werden
>>> from scipy.spatial import Delaunay
>>> import numpy as np
>>> points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
>>> tri = Delaunay(points)
Wir können sie visualisieren
>>> import matplotlib.pyplot as plt
>>> plt.triplot(points[:,0], points[:,1], tri.simplices)
>>> plt.plot(points[:,0], points[:,1], 'o')
Und einige weitere Verzierungen hinzufügen
>>> for j, p in enumerate(points):
... plt.text(p[0]-0.03, p[1]+0.03, j, ha='right') # label the points
>>> for j, s in enumerate(tri.simplices):
... p = points[s].mean(axis=0)
... plt.text(p[0], p[1], '#%d' % j, ha='center') # label triangles
>>> plt.xlim(-0.5, 1.5); plt.ylim(-0.5, 1.5)
>>> plt.show()
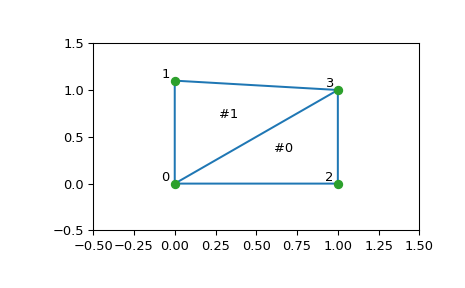
Die Struktur der Triangulation wird wie folgt kodiert: Das Attribut simplices enthält die Indizes der Punkte im Array points, die das Dreieck bilden. Zum Beispiel
>>> i = 1
>>> tri.simplices[i,:]
array([3, 1, 0], dtype=int32)
>>> points[tri.simplices[i,:]]
array([[ 1. , 1. ],
[ 0. , 1.1],
[ 0. , 0. ]])
Darüber hinaus können auch benachbarte Dreiecke gefunden werden
>>> tri.neighbors[i]
array([-1, 0, -1], dtype=int32)
Dies sagt uns, dass dieses Dreieck das Dreieck Nr. 0 als Nachbar hat, aber keine anderen Nachbarn. Darüber hinaus sagt es uns, dass der Nachbar 0 gegenüber der Ecke 1 des Dreiecks liegt
>>> points[tri.simplices[i, 1]]
array([ 0. , 1.1])
Tatsächlich sehen wir aus der Abbildung, dass dies der Fall ist.
Qhull kann auch Tessellationen zu Simplices für höherdimensionale Punktmengen durchführen (z. B. Unterteilung in Tetraeder in 3D).
Koplanare Punkte#
Es ist wichtig zu beachten, dass nicht *alle* Punkte notwendigerweise als Eckpunkte der Triangulation erscheinen, aufgrund von Problemen mit der numerischen Präzision bei der Bildung der Triangulation. Betrachten Sie das obige Beispiel mit einem duplizierten Punkt
>>> points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
>>> tri = Delaunay(points)
>>> np.unique(tri.simplices.ravel())
array([0, 1, 2, 3], dtype=int32)
Beachten Sie, dass Punkt Nr. 4, der ein Duplikat ist, nicht als Eckpunkt der Triangulation vorkommt. Dass dies geschah, wird aufgezeichnet
>>> tri.coplanar
array([[4, 0, 3]], dtype=int32)
Das bedeutet, dass Punkt 4 nahe dem Dreieck 0 und der Ecke 3 liegt, aber nicht in die Triangulation einbezogen wird.
Beachten Sie, dass solche Degenerationen nicht nur aufgrund von duplizierten Punkten auftreten können, sondern auch aus komplizierteren geometrischen Gründen, selbst bei Punktmengen, die auf den ersten Blick gutartig erscheinen.
Qhull verfügt jedoch über die Option "QJ", die es anweist, die Eingabedaten zufällig zu stören, bis Degenerationen behoben sind
>>> tri = Delaunay(points, qhull_options="QJ Pp")
>>> points[tri.simplices]
array([[[1, 0],
[1, 1],
[0, 0]],
[[1, 1],
[1, 1],
[1, 0]],
[[1, 1],
[0, 1],
[0, 0]],
[[0, 1],
[1, 1],
[1, 1]]])
Es erschienen zwei neue Dreiecke. Wir sehen jedoch, dass sie degeneriert sind und eine Fläche von Null haben.
Konvexe Hüllen#
Eine konvexe Hülle ist das kleinste konvexe Objekt, das alle Punkte einer gegebenen Punktmenge enthält.
Diese können über die Qhull-Wrapper in scipy.spatial wie folgt berechnet werden
>>> from scipy.spatial import ConvexHull
>>> rng = np.random.default_rng()
>>> points = rng.random((30, 2)) # 30 random points in 2-D
>>> hull = ConvexHull(points)
Die konvexe Hülle wird als eine Menge von N 1-dimensionalen Simplices dargestellt, was in 2D Liniensegmente bedeutet. Das Speicherformat ist genau dasselbe wie bei den Simplices in der oben diskutierten Delaunay-Triangulation.
Wir können das obige Ergebnis veranschaulichen
>>> import matplotlib.pyplot as plt
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> for simplex in hull.simplices:
... plt.plot(points[simplex,0], points[simplex,1], 'k-')
>>> plt.show()
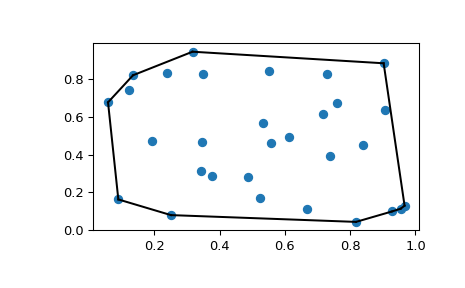
Das Gleiche kann mit scipy.spatial.convex_hull_plot_2d erreicht werden.
Voronoi-Diagramme#
Ein Voronoi-Diagramm ist eine Unterteilung des Raumes in die nächsten Umgebungen einer gegebenen Menge von Punkten.
Es gibt zwei Möglichkeiten, sich diesem Objekt mit scipy.spatial zu nähern. Erstens kann man die KDTree verwenden, um die Frage "welcher der Punkte ist diesem am nächsten" zu beantworten, und die Regionen auf diese Weise definieren
>>> from scipy.spatial import KDTree
>>> points = np.array([[0, 0], [0, 1], [0, 2], [1, 0], [1, 1], [1, 2],
... [2, 0], [2, 1], [2, 2]])
>>> tree = KDTree(points)
>>> tree.query([0.1, 0.1])
(0.14142135623730953, 0)
Der Punkt (0.1, 0.1) gehört also zur Region 0. In Farbe
>>> x = np.linspace(-0.5, 2.5, 31)
>>> y = np.linspace(-0.5, 2.5, 33)
>>> xx, yy = np.meshgrid(x, y)
>>> xy = np.c_[xx.ravel(), yy.ravel()]
>>> import matplotlib.pyplot as plt
>>> dx_half, dy_half = np.diff(x[:2])[0] / 2., np.diff(y[:2])[0] / 2.
>>> x_edges = np.concatenate((x - dx_half, [x[-1] + dx_half]))
>>> y_edges = np.concatenate((y - dy_half, [y[-1] + dy_half]))
>>> plt.pcolormesh(x_edges, y_edges, tree.query(xy)[1].reshape(33, 31), shading='flat')
>>> plt.plot(points[:,0], points[:,1], 'ko')
>>> plt.show()
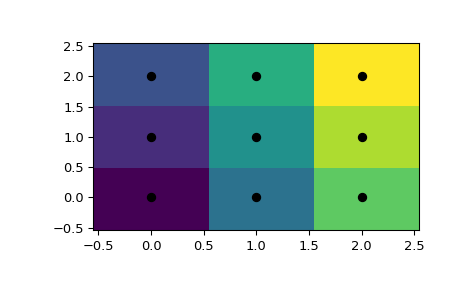
Dies gibt jedoch nicht das Voronoi-Diagramm als geometrisches Objekt wieder.
Die Darstellung in Form von Linien und Punkten kann wieder über die Qhull-Wrapper in scipy.spatial erhalten werden
>>> from scipy.spatial import Voronoi
>>> vor = Voronoi(points)
>>> vor.vertices
array([[0.5, 0.5],
[0.5, 1.5],
[1.5, 0.5],
[1.5, 1.5]])
Die Voronoi-Eckpunkte bezeichnen die Menge der Punkte, die die polygonalen Kanten der Voronoi-Regionen bilden. In diesem Fall gibt es 9 verschiedene Regionen
>>> vor.regions
[[], [-1, 0], [-1, 1], [1, -1, 0], [3, -1, 2], [-1, 3], [-1, 2], [0, 1, 3, 2], [2, -1, 0], [3, -1, 1]]
Der negative Wert -1 zeigt wieder einen Punkt im Unendlichen an. Tatsächlich ist nur eine der Regionen, [0, 1, 3, 2], begrenzt. Beachten Sie hier, dass aufgrund ähnlicher Probleme mit der numerischen Präzision wie bei der Delaunay-Triangulation oben möglicherweise weniger Voronoi-Regionen als Eingabepunkte vorhanden sind.
Die Kämme (Linien in 2D), die die Regionen trennen, werden als eine ähnliche Sammlung von Simplices wie die Stücke der konvexen Hülle beschrieben
>>> vor.ridge_vertices
[[-1, 0], [-1, 0], [-1, 1], [-1, 1], [0, 1], [-1, 3], [-1, 2], [2, 3], [-1, 3], [-1, 2], [1, 3], [0, 2]]
Diese Zahlen stellen die Indizes der Voronoi-Eckpunkte dar, die die Liniensegmente bilden. -1 ist wieder ein Punkt im Unendlichen – nur 4 der 12 Linien sind begrenzte Liniensegmente, während andere ins Unendliche reichen.
Die Voronoi-Kämme stehen senkrecht zu den Linien, die zwischen den Eingabepunkten gezogen werden. Zu welchen beiden Punkten jeder Kamm gehört, wird ebenfalls aufgezeichnet
>>> vor.ridge_points
array([[0, 3],
[0, 1],
[2, 5],
[2, 1],
[1, 4],
[7, 8],
[7, 6],
[7, 4],
[8, 5],
[6, 3],
[4, 5],
[4, 3]], dtype=int32)
Diese Informationen zusammen reichen aus, um das vollständige Diagramm zu konstruieren.
Wir können es wie folgt zeichnen. Zuerst die Punkte und die Voronoi-Eckpunkte
>>> plt.plot(points[:, 0], points[:, 1], 'o')
>>> plt.plot(vor.vertices[:, 0], vor.vertices[:, 1], '*')
>>> plt.xlim(-1, 3); plt.ylim(-1, 3)
Das Zeichnen der endlichen Liniensegmente erfolgt wie bei der konvexen Hülle, aber jetzt müssen wir die unendlichen Kanten berücksichtigen
>>> for simplex in vor.ridge_vertices:
... simplex = np.asarray(simplex)
... if np.all(simplex >= 0):
... plt.plot(vor.vertices[simplex, 0], vor.vertices[simplex, 1], 'k-')
Die ins Unendliche reichenden Kämme erfordern etwas mehr Sorgfalt
>>> center = points.mean(axis=0)
>>> for pointidx, simplex in zip(vor.ridge_points, vor.ridge_vertices):
... simplex = np.asarray(simplex)
... if np.any(simplex < 0):
... i = simplex[simplex >= 0][0] # finite end Voronoi vertex
... t = points[pointidx[1]] - points[pointidx[0]] # tangent
... t = t / np.linalg.norm(t)
... n = np.array([-t[1], t[0]]) # normal
... midpoint = points[pointidx].mean(axis=0)
... far_point = vor.vertices[i] + np.sign(np.dot(midpoint - center, n)) * n * 100
... plt.plot([vor.vertices[i,0], far_point[0]],
... [vor.vertices[i,1], far_point[1]], 'k--')
>>> plt.show()
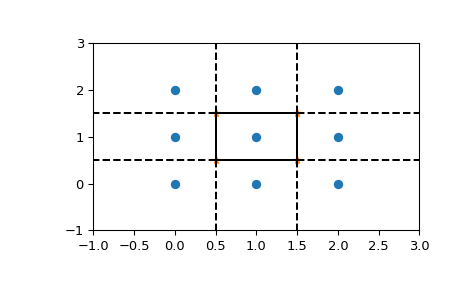
Diese Abbildung kann auch mit scipy.spatial.voronoi_plot_2d erstellt werden.
Voronoi-Diagramme können zur Erstellung interessanter generativer Kunst verwendet werden. Experimentieren Sie mit den Einstellungen dieser mandala-Funktion, um Ihre eigene zu erstellen!
>>> import numpy as np
>>> from scipy import spatial
>>> import matplotlib.pyplot as plt
>>> def mandala(n_iter, n_points, radius):
... """Creates a mandala figure using Voronoi tessellations.
...
... Parameters
... ----------
... n_iter : int
... Number of iterations, i.e. how many times the equidistant points will
... be generated.
... n_points : int
... Number of points to draw per iteration.
... radius : scalar
... The radial expansion factor.
...
... Returns
... -------
... fig : matplotlib.Figure instance
...
... Notes
... -----
... This code is adapted from the work of Audrey Roy Greenfeld [1]_ and Carlos
... Focil-Espinosa [2]_, who created beautiful mandalas with Python code. That
... code in turn was based on Antonio Sánchez Chinchón's R code [3]_.
...
... References
... ----------
... .. [1] https://www.codemakesmehappy.com/2019/09/voronoi-mandalas.html
...
... .. [2] https://github.com/CarlosFocil/mandalapy
...
... .. [3] https://github.com/aschinchon/mandalas
...
... """
... fig = plt.figure(figsize=(10, 10))
... ax = fig.add_subplot(111)
... ax.set_axis_off()
... ax.set_aspect('equal', adjustable='box')
...
... angles = np.linspace(0, 2*np.pi * (1 - 1/n_points), num=n_points) + np.pi/2
... # Starting from a single center point, add points iteratively
... xy = np.array([[0, 0]])
... for k in range(n_iter):
... t1 = np.array([])
... t2 = np.array([])
... # Add `n_points` new points around each existing point in this iteration
... for i in range(xy.shape[0]):
... t1 = np.append(t1, xy[i, 0] + radius**k * np.cos(angles))
... t2 = np.append(t2, xy[i, 1] + radius**k * np.sin(angles))
...
... xy = np.column_stack((t1, t2))
...
... # Create the Mandala figure via a Voronoi plot
... spatial.voronoi_plot_2d(spatial.Voronoi(xy), ax=ax)
...
... return fig
>>> # Modify the following parameters in order to get different figures
>>> n_iter = 3
>>> n_points = 6
>>> radius = 4
>>> fig = mandala(n_iter, n_points, radius)
>>> plt.show()