Fourier-Transformationen (scipy.fft)#
Die Fourier-Analyse ist eine Methode, um eine Funktion als Summe periodischer Komponenten auszudrücken und um das Signal aus diesen Komponenten wiederherzustellen. Wenn sowohl die Funktion als auch ihre Fourier-Transformation durch diskretisierte Entsprechungen ersetzt werden, nennt man dies die diskrete Fourier-Transformation (DFT). Die DFT ist zu einem Eckpfeiler des numerischen Rechnens geworden, teilweise wegen eines sehr schnellen Algorithmus zu ihrer Berechnung, genannt Fast Fourier Transform (FFT), der Gauss (1805) bekannt war und in seiner heutigen Form von Cooley und Tukey [CT65] veröffentlicht wurde. Press et al. [NR07] bieten eine zugängliche Einführung in die Fourier-Analyse und ihre Anwendungen.
Schnelle Fourier-Transformationen#
1-D Diskrete Fourier-Transformationen#
Die FFT y[k] der Länge \(N\) der Sequenz x[n] der Länge \(N\) ist definiert als
und die inverse Transformation ist wie folgt definiert
Diese Transformationen können mit Hilfe von fft und ifft berechnet werden, wie im folgenden Beispiel gezeigt.
>>> from scipy.fft import fft, ifft
>>> import numpy as np
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
>>> y = fft(x)
>>> y
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])
>>> yinv = ifft(y)
>>> yinv
array([ 1.0+0.j, 2.0+0.j, 1.0+0.j, -1.0+0.j, 1.5+0.j])
Aus der Definition der FFT lässt sich erkennen, dass
Im Beispiel
>>> np.sum(x)
4.5
entspricht \(y[0]\). Für gerades N enthalten die Elemente \(y[1]...y[N/2-1]\) die positiven Frequenzterme, und die Elemente \(y[N/2]...y[N-1]\) enthalten die negativen Frequenzterme, in absteigender Reihenfolge negativer Frequenzen. Für ungerades N enthalten die Elemente \(y[1]...y[(N-1)/2]\) die positiven Frequenzterme, und die Elemente \(y[(N+1)/2]...y[N-1]\) enthalten die negativen Frequenzterme, in absteigender Reihenfolge negativer Frequenzen.
Wenn die Sequenz x reellwertig ist, sind die Werte von \(y[n]\) für positive Frequenzen die Konjugierte der Werte \(y[n]\) für negative Frequenzen (da das Spektrum symmetrisch ist). Typischerweise wird nur die FFT, die positiven Frequenzen entspricht, geplottet.
Das Beispiel plottet die FFT der Summe zweier Sinuswellen.
>>> from scipy.fft import fft, fftfreq
>>> import numpy as np
>>> # Number of sample points
>>> N = 600
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
>>> yf = fft(y)
>>> xf = fftfreq(N, T)[:N//2]
>>> import matplotlib.pyplot as plt
>>> plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
>>> plt.grid()
>>> plt.show()
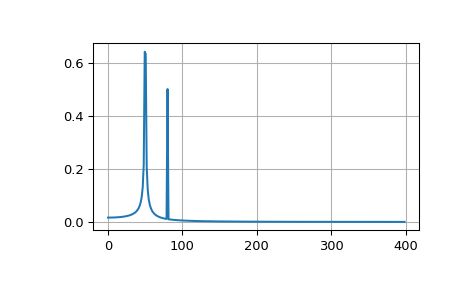
Das FFT-Eingangssignal wird inhärent abgeschnitten. Dieser Abschneideeffekt kann als Multiplikation eines unendlichen Signals mit einer rechteckigen Fensterfunktion modelliert werden. Im Spektralbereich wird diese Multiplikation zu einer Faltung des Signal-Spektrums mit dem Spektrum der Fensterfunktion, das die Form \(\sin(x)/x\) hat. Diese Faltung ist die Ursache für den Effekt namens spektrale Leckage (siehe [WPW]). Die Fensterung des Signals mit einer dedizierten Fensterfunktion hilft, die spektrale Leckage zu mindern. Das folgende Beispiel verwendet ein Blackman-Fenster aus scipy.signal und zeigt den Effekt der Fensterung (die Nullkomponente der FFT wurde zu Illustrationszwecken abgeschnitten).
>>> from scipy.fft import fft, fftfreq
>>> import numpy as np
>>> # Number of sample points
>>> N = 600
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
>>> yf = fft(y)
>>> from scipy.signal.windows import blackman
>>> w = blackman(N)
>>> ywf = fft(y*w)
>>> xf = fftfreq(N, T)[:N//2]
>>> import matplotlib.pyplot as plt
>>> plt.semilogy(xf[1:N//2], 2.0/N * np.abs(yf[1:N//2]), '-b')
>>> plt.semilogy(xf[1:N//2], 2.0/N * np.abs(ywf[1:N//2]), '-r')
>>> plt.legend(['FFT', 'FFT w. window'])
>>> plt.grid()
>>> plt.show()
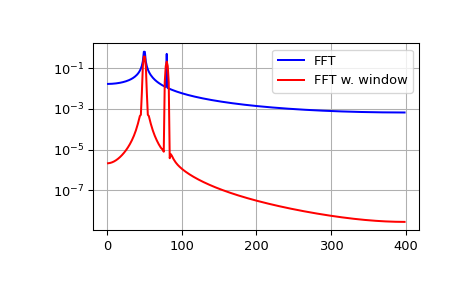
Wenn die Sequenz x komplexwertig ist, ist das Spektrum nicht mehr symmetrisch. Um die Arbeit mit den FFT-Funktionen zu vereinfachen, stellt SciPy die folgenden beiden Hilfsfunktionen zur Verfügung.
Die Funktion fftfreq gibt die FFT-Abtastfrequenzpunkte zurück.
>>> from scipy.fft import fftfreq
>>> freq = fftfreq(8, 0.125)
>>> freq
array([ 0., 1., 2., 3., -4., -3., -2., -1.])
In ähnlicher Weise ermöglicht die Funktion fftshift das Vertauschen der unteren und oberen Hälften eines Vektors, so dass dieser für die Anzeige geeignet ist.
>>> from scipy.fft import fftshift
>>> x = np.arange(8)
>>> fftshift(x)
array([4, 5, 6, 7, 0, 1, 2, 3])
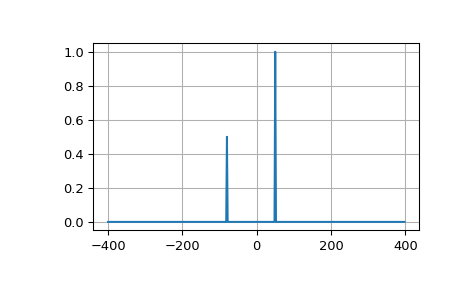
Das folgende Beispiel plottet die FFT zweier komplexer Exponentialfunktionen; beachten Sie das asymmetrische Spektrum.
>>> from scipy.fft import fft, fftfreq, fftshift
>>> import numpy as np
>>> # number of signal points
>>> N = 400
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.exp(50.0 * 1.j * 2.0*np.pi*x) + 0.5*np.exp(-80.0 * 1.j * 2.0*np.pi*x)
>>> yf = fft(y)
>>> xf = fftfreq(N, T)
>>> xf = fftshift(xf)
>>> yplot = fftshift(yf)
>>> import matplotlib.pyplot as plt
>>> plt.plot(xf, 1.0/N * np.abs(yplot))
>>> plt.grid()
>>> plt.show()
Die Funktion rfft berechnet die FFT einer reellen Sequenz und gibt die komplexen FFT-Koeffizienten \(y[n]\) nur für die Hälfte des Frequenzbereichs aus. Die verbleibenden negativen Frequenzkomponenten sind durch die hermitesche Symmetrie der FFT für eine reelle Eingabe impliziert (y[n] = conj(y[-n])). Bei geradem N: \([Re(y[0]) + 0j, y[1], ..., Re(y[N/2]) + 0j]\); bei ungeradem N \([Re(y[0]) + 0j, y[1], ..., y[N/2]\). Die explizit als \(Re(y[k]) + 0j\) dargestellten Terme sind auf rein reell beschränkt, da sie aufgrund der hermiteschen Eigenschaft ihre eigene komplexe Konjugierte sind.
Die entsprechende Funktion irfft berechnet die IFFT der FFT-Koeffizienten mit dieser speziellen Reihenfolge.
>>> from scipy.fft import fft, rfft, irfft
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5, 1.0])
>>> fft(x)
array([ 5.5 +0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 +0.j , -2.75+1.29903811j, 2.25+0.4330127j ])
>>> yr = rfft(x)
>>> yr
array([ 5.5 +0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 +0.j ])
>>> irfft(yr)
array([ 1. , 2. , 1. , -1. , 1.5, 1. ])
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
>>> fft(x)
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])
>>> yr = rfft(x)
>>> yr
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j])
Beachten Sie, dass die rfft von ungeraden und geraden Längensignalen die gleiche Form haben. Standardmäßig nimmt irfft an, dass das Ausgabesignal eine gerade Länge haben soll. Für ungerade Signale liefert es daher ein falsches Ergebnis.
>>> irfft(yr)
array([ 1.70788987, 2.40843925, -0.37366961, 0.75734049])
Um das ursprüngliche Signal ungerader Länge wiederherzustellen, **müssen** wir die Ausgabegröße über den Parameter n übergeben.
>>> irfft(yr, n=len(x))
array([ 1. , 2. , 1. , -1. , 1.5])
2- und N-D Diskrete Fourier-Transformationen#
Die Funktionen fft2 und ifft2 stellen 2-D FFT bzw. IFFT zur Verfügung. Ebenso stellen fftn und ifftn N-D FFT bzw. IFFT zur Verfügung.
Für reellwertige Eingangssignale gibt es, analog zu rfft, die Funktionen rfft2 und irfft2 für 2-D reelle Transformationen; rfftn und irfftn für N-D reelle Transformationen.
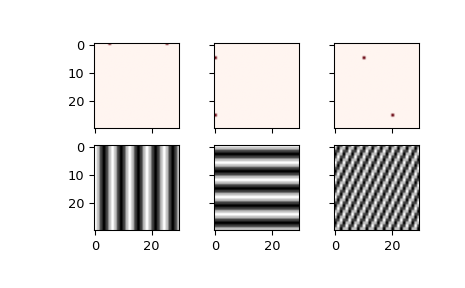
Das folgende Beispiel demonstriert eine 2-D IFFT und plottet die resultierenden (2-D) Zeitbereichssignale.
>>> from scipy.fft import ifftn
>>> import matplotlib.pyplot as plt
>>> import matplotlib.cm as cm
>>> import numpy as np
>>> N = 30
>>> f, ((ax1, ax2, ax3), (ax4, ax5, ax6)) = plt.subplots(2, 3, sharex='col', sharey='row')
>>> xf = np.zeros((N,N))
>>> xf[0, 5] = 1
>>> xf[0, N-5] = 1
>>> Z = ifftn(xf)
>>> ax1.imshow(xf, cmap=cm.Reds)
>>> ax4.imshow(np.real(Z), cmap=cm.gray)
>>> xf = np.zeros((N, N))
>>> xf[5, 0] = 1
>>> xf[N-5, 0] = 1
>>> Z = ifftn(xf)
>>> ax2.imshow(xf, cmap=cm.Reds)
>>> ax5.imshow(np.real(Z), cmap=cm.gray)
>>> xf = np.zeros((N, N))
>>> xf[5, 10] = 1
>>> xf[N-5, N-10] = 1
>>> Z = ifftn(xf)
>>> ax3.imshow(xf, cmap=cm.Reds)
>>> ax6.imshow(np.real(Z), cmap=cm.gray)
>>> plt.show()
Diskrete Kosinustransformationen#
SciPy bietet eine DCT mit der Funktion dct und eine entsprechende IDCT mit der Funktion idct. Es gibt 8 Arten der DCT [WPC], [Mak]; jedoch sind in SciPy nur die ersten 4 Typen implementiert. "Die" DCT bezieht sich im Allgemeinen auf DCT Typ 2, und "die" Inverse DCT auf DCT Typ 3. Zusätzlich können die DCT-Koeffizienten unterschiedlich normiert werden (für die meisten Typen bietet SciPy None und ortho). Zwei Parameter der dct/idct Funktionsaufrufe ermöglichen die Einstellung des DCT-Typs und der Koeffizienten-Normalisierung.
Für ein eindimensionales Array x ist dct(x, norm='ortho') gleich MATLAB dct(x).
Typ I DCT#
SciPy verwendet die folgende Definition der unnormierten DCT-I (norm=None)
Beachten Sie, dass DCT-I nur für Eingabegrößen > 1 unterstützt wird.
Typ II DCT#
SciPy verwendet die folgende Definition der unnormierten DCT-II (norm=None)
Im Fall der normierten DCT (norm='ortho') werden die DCT-Koeffizienten \(y[k]\) mit einem Skalierungsfaktor f multipliziert.
In diesem Fall werden die DCT-Basis"funktionen" \(\phi_k[n] = 2 f \cos \left({\pi(2n+1)k \over 2N} \right)\) orthonormal.
Typ III DCT#
SciPy verwendet die folgende Definition der unnormierten DCT-III (norm=None)
oder für norm='ortho'
Typ IV DCT#
SciPy verwendet die folgende Definition der unnormierten DCT-IV (norm=None)
oder für norm='ortho'
DCT und IDCT#
Die (unnormierte) DCT-III ist die Inverse der (unnormierten) DCT-II, bis auf einen Faktor von 2N. Die orthonormalisierte DCT-III ist exakt die Inverse der orthonormalisierten DCT-II. Die Funktion idct übernimmt die Abbildungen zwischen den DCT- und IDCT-Typen sowie die korrekte Normalisierung.
Das folgende Beispiel zeigt die Beziehung zwischen DCT und IDCT für verschiedene Typen und Normalisierungen.
>>> from scipy.fft import dct, idct
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
Die DCT-II und DCT-III sind gegenseitige Inverse, daher kehren wir bei einer orthonormalen Transformation zum ursprünglichen Signal zurück.
>>> dct(dct(x, type=2, norm='ortho'), type=3, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
Wenn wir dasselbe unter der Standardnormalisierung tun, erhalten wir jedoch einen zusätzlichen Skalierungsfaktor von \(2N=10\), da die Vorwärtstransformation unnormiert ist.
>>> dct(dct(x, type=2), type=3)
array([ 10., 20., 10., -10., 15.])
Aus diesem Grund sollten wir die Funktion idct verwenden, wobei für beide derselbe Typ verwendet wird, was zu einem korrekt normierten Ergebnis führt.
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=2), type=2)
array([ 1. , 2. , 1. , -1. , 1.5])
Analoge Ergebnisse können für DCT-I beobachtet werden, die bis auf einen Faktor von \(2(N-1)\) ihre eigene Inverse ist.
>>> dct(dct(x, type=1, norm='ortho'), type=1, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # Unnormalized round-trip via DCT-I: scaling factor 2*(N-1) = 8
>>> dct(dct(x, type=1), type=1)
array([ 8. , 16., 8. , -8. , 12.])
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=1), type=1)
array([ 1. , 2. , 1. , -1. , 1.5])
Und für DCT-IV, die ebenfalls bis auf einen Faktor von \(2N\) ihre eigene Inverse ist.
>>> dct(dct(x, type=4, norm='ortho'), type=4, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # Unnormalized round-trip via DCT-IV: scaling factor 2*N = 10
>>> dct(dct(x, type=4), type=4)
array([ 10., 20., 10., -10., 15.])
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=4), type=4)
array([ 1. , 2. , 1. , -1. , 1.5])
Beispiel#
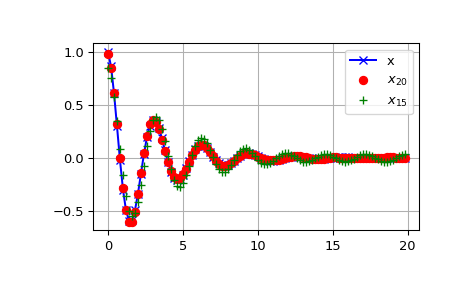
Die DCT weist die "Energiekompressionseigenschaft" auf, was bedeutet, dass bei vielen Signalen nur die ersten wenigen DCT-Koeffizienten eine signifikante Größe haben. Das Nullsetzen der anderen Koeffizienten führt zu einem geringen Rekonstruktionsfehler, eine Tatsache, die bei verlustbehafteter Signal-Kompression (z. B. JPEG-Kompression) ausgenutzt wird.
Das folgende Beispiel zeigt ein Signal x und zwei Rekonstruktionen (\(x_{20}\) und \(x_{15}\)) aus den DCT-Koeffizienten des Signals. Das Signal \(x_{20}\) wird aus den ersten 20 DCT-Koeffizienten rekonstruiert, \(x_{15}\) aus den ersten 15 DCT-Koeffizienten. Es ist ersichtlich, dass der relative Fehler bei Verwendung von 20 Koeffizienten immer noch sehr gering ist (ca. 0,1 %), aber eine fünfmal höhere Kompressionsrate bietet.
>>> from scipy.fft import dct, idct
>>> import matplotlib.pyplot as plt
>>> N = 100
>>> t = np.linspace(0,20,N, endpoint=False)
>>> x = np.exp(-t/3)*np.cos(2*t)
>>> y = dct(x, norm='ortho')
>>> window = np.zeros(N)
>>> window[:20] = 1
>>> yr = idct(y*window, norm='ortho')
>>> sum(abs(x-yr)**2) / sum(abs(x)**2)
0.0009872817275276098
>>> plt.plot(t, x, '-bx')
>>> plt.plot(t, yr, 'ro')
>>> window = np.zeros(N)
>>> window[:15] = 1
>>> yr = idct(y*window, norm='ortho')
>>> sum(abs(x-yr)**2) / sum(abs(x)**2)
0.06196643004256714
>>> plt.plot(t, yr, 'g+')
>>> plt.legend(['x', '$x_{20}$', '$x_{15}$'])
>>> plt.grid()
>>> plt.show()
Diskrete Sinustransformationen#
SciPy stellt eine DST [Mak] mit der Funktion dst und eine entsprechende IDST mit der Funktion idst zur Verfügung.
Es gibt theoretisch 8 Arten der DST für verschiedene Kombinationen von geraden/ungeraden Randbedingungen und Randverschiebungen [WPS]; in SciPy sind nur die ersten 4 Typen implementiert.
Typ I DST#
DST-I geht davon aus, dass die Eingabe bei n=-1 und n=N ungerade ist. SciPy verwendet die folgende Definition der unnormierten DST-I (norm=None)
Beachten Sie auch, dass DST-I nur für Eingabegrößen > 1 unterstützt wird. Die (unnormierte) DST-I ist bis auf einen Faktor von 2(N+1) ihre eigene Inverse.
Typ II DST#
DST-II geht davon aus, dass die Eingabe bei n=-1/2 ungerade und bei n=N gerade ist. SciPy verwendet die folgende Definition der unnormierten DST-II (norm=None)
Typ III DST#
DST-III geht davon aus, dass die Eingabe bei n=-1 ungerade und bei n=N-1 gerade ist. SciPy verwendet die folgende Definition der unnormierten DST-III (norm=None)
Typ IV DST#
SciPy verwendet die folgende Definition der unnormierten DST-IV (norm=None)
oder für norm='ortho'
DST und IDST#
Das folgende Beispiel zeigt die Beziehung zwischen DST und IDST für verschiedene Typen und Normalisierungen.
>>> from scipy.fft import dst, idst
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
Die DST-II und DST-III sind gegenseitige Inverse, daher kehren wir bei einer orthonormalen Transformation zum ursprünglichen Signal zurück.
>>> dst(dst(x, type=2, norm='ortho'), type=3, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
Wenn wir dasselbe unter der Standardnormalisierung tun, erhalten wir jedoch einen zusätzlichen Skalierungsfaktor von \(2N=10\), da die Vorwärtstransformation unnormiert ist.
>>> dst(dst(x, type=2), type=3)
array([ 10., 20., 10., -10., 15.])
Aus diesem Grund sollten wir die Funktion idst verwenden, wobei für beide derselbe Typ verwendet wird, was zu einem korrekt normierten Ergebnis führt.
>>> idst(dst(x, type=2), type=2)
array([ 1. , 2. , 1. , -1. , 1.5])
Analoge Ergebnisse können für DST-I beobachtet werden, die bis auf einen Faktor von \(2(N-1)\) ihre eigene Inverse ist.
>>> dst(dst(x, type=1, norm='ortho'), type=1, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # scaling factor 2*(N+1) = 12
>>> dst(dst(x, type=1), type=1)
array([ 12., 24., 12., -12., 18.])
>>> # no scaling factor
>>> idst(dst(x, type=1), type=1)
array([ 1. , 2. , 1. , -1. , 1.5])
Und für DST-IV, die ebenfalls bis auf einen Faktor von \(2N\) ihre eigene Inverse ist.
>>> dst(dst(x, type=4, norm='ortho'), type=4, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # scaling factor 2*N = 10
>>> dst(dst(x, type=4), type=4)
array([ 10., 20., 10., -10., 15.])
>>> # no scaling factor
>>> idst(dst(x, type=4), type=4)
array([ 1. , 2. , 1. , -1. , 1.5])
Schnelle Hankel-Transformation#
SciPy bietet die Funktionen fht und ifht, um die Schnelle Hankel-Transformation (FHT) und ihre Inverse (IFHT) auf logarithmisch verteilten Eingabearrays durchzuführen.
Die FHT ist die diskretisierte Version der kontinuierlichen Hankel-Transformation, die von [Ham00] definiert wird.
mit \(J_{\mu}\) als Bessel-Funktion der Ordnung \(\mu\). Unter einer Variablenänderung von \(r \to \log r\) und \(k \to \log k\) wird dies zu
was eine Faltung im logarithmischen Raum darstellt. Der FHT-Algorithmus verwendet die FFT, um diese Faltung auf diskreten Eingabedaten durchzuführen.
Es muss darauf geachtet werden, numerische Ringeffekte aufgrund der zirkulären Natur der FFT-Faltung zu minimieren. Um sicherzustellen, dass die Bedingung für geringe Ringeffekte [Ham00] erfüllt ist, kann das Ausgabearray leicht mit einem Offset verschoben werden, der mit der Funktion fhtoffset berechnet wird.
Referenzen#
Cooley, James W., und John W. Tukey, 1965, „An algorithm for the machine calculation of complex Fourier series“, Math. Comput. 19: 297-301.
Press, W., Teukolsky, S., Vetterline, W.T., und Flannery, B.P., 2007, Numerical Recipes: The Art of Scientific Computing, Kap. 12-13. Cambridge Univ. Press, Cambridge, UK.
J. Makhoul, 1980, „A Fast Cosine Transform in One and Two Dimensions“, IEEE Transactions on acoustics, speech and signal processing Bd. 28(1), S. 27-34, DOI:10.1109/TASSP.1980.1163351
A. J. S. Hamilton, 2000, „Uncorrelated modes of the non-linear power spectrum“, MNRAS, 312, 257. DOI:10.1046/j.1365-8711.2000.03071.x