Multidimensionale Bildverarbeitung (scipy.ndimage)#
Einleitung#
Bildverarbeitung und -analyse werden im Allgemeinen als Operationen auf 2-D-Arrays von Werten betrachtet. Es gibt jedoch eine Reihe von Bereichen, in denen Bilder höherer Dimensionalität analysiert werden müssen. Gute Beispiele hierfür sind die medizinische und biologische Bildgebung. numpy eignet sich aufgrund seiner inhärenten multidimensionalen Natur sehr gut für diese Art von Anwendungen. Das Paket scipy.ndimage bietet eine Reihe von allgemeinen Funktionen zur Bildverarbeitung und -analyse, die für den Betrieb mit Arrays beliebiger Dimensionalität konzipiert sind. Das Paket umfasst derzeit: Funktionen für lineare und nichtlineare Filterung, binäre Morphologie, B-Spline-Interpolation und Objektmessungen.
Filterfunktionen#
Die in diesem Abschnitt beschriebenen Funktionen führen alle eine Art von räumlicher Filterung des Eingabe-Arrays durch: die Elemente in der Ausgabe sind eine Funktion der Werte in der Nachbarschaft des entsprechenden Eingabeelements. Wir bezeichnen diese Nachbarschaft von Elementen als Filterkern, der oft rechteckig ist, aber auch eine beliebige Fußabdruckform haben kann. Viele der unten beschriebenen Funktionen erlauben es Ihnen, den Fußabdruck des Kerns zu definieren, indem Sie eine Maske über den Parameter footprint übergeben. Zum Beispiel kann ein kreuzförmiger Kern wie folgt definiert werden
>>> footprint = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> footprint
array([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]])
Normalerweise befindet sich der Ursprung des Kerns in der Mitte, die durch Division der Dimensionen der Kernform durch zwei berechnet wird. Zum Beispiel befindet sich der Ursprung eines 1-D-Kerns der Länge drei am zweiten Element. Nehmen Sie zum Beispiel die Korrelation eines 1-D-Arrays mit einem Filter der Länge 3, der aus Einsen besteht
>>> from scipy.ndimage import correlate1d
>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1])
array([0, 0, 1, 1, 1, 0, 0])
Manchmal ist es praktisch, einen anderen Ursprung für den Kern zu wählen. Aus diesem Grund unterstützen die meisten Funktionen den Parameter origin, der den Ursprung des Filters relativ zu seinem Zentrum angibt. Zum Beispiel
>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1], origin = -1)
array([0, 1, 1, 1, 0, 0, 0])
Dies hat den Effekt einer Verschiebung des Ergebnisses nach links. Dieses Merkmal wird nicht sehr oft benötigt, kann aber nützlich sein, insbesondere für Filter mit gerader Größe. Ein gutes Beispiel ist die Berechnung von Rückwärts- und Vorwärtsdifferenzen
>>> a = [0, 0, 1, 1, 1, 0, 0]
>>> correlate1d(a, [-1, 1]) # backward difference
array([ 0, 0, 1, 0, 0, -1, 0])
>>> correlate1d(a, [-1, 1], origin = -1) # forward difference
array([ 0, 1, 0, 0, -1, 0, 0])
Wir hätten die Vorwärtsdifferenz auch wie folgt berechnen können
>>> correlate1d(a, [0, -1, 1])
array([ 0, 1, 0, 0, -1, 0, 0])
Die Verwendung des origin-Parameters anstelle eines größeren Kerns ist jedoch effizienter. Für multidimensionale Kerne kann origin eine Zahl sein, in diesem Fall wird angenommen, dass der Ursprung entlang aller Achsen gleich ist, oder eine Sequenz, die den Ursprung entlang jeder Achse angibt.
Da die Ausgabeelemente eine Funktion der Elemente in der Nachbarschaft der Eingabeelemente sind, müssen die Ränder des Arrays entsprechend behandelt werden, indem Werte außerhalb der Ränder bereitgestellt werden. Dies geschieht durch die Annahme, dass die Arrays über ihre Grenzen hinaus gemäß bestimmten Randbedingungen erweitert werden. In den unten beschriebenen Funktionen können die Randbedingungen über den Parameter mode ausgewählt werden, der ein String mit dem Namen der Randbedingung sein muss. Die folgenden Randbedingungen werden derzeit unterstützt
mode
Beschreibung
Beispiel
„nearest“
Verwenden Sie den Wert am Rand
[1 2 3]->[1 1 2 3 3]
„wrap“
Periodische Replikation des Arrays
[1 2 3]->[3 1 2 3 1]
„reflect“
Spiegeln Sie das Array am Rand
[1 2 3]->[1 1 2 3 3]
„mirror“
Spiegeln Sie das Array am Rand
[1 2 3]->[2 1 2 3 2]
„constant“
Verwenden Sie einen konstanten Wert, Standard ist 0,0
[1 2 3]->[0 1 2 3 0]
Die folgenden Synonyme werden ebenfalls aus Konsistenzgründen mit den Interpolationsroutinen unterstützt
mode
Beschreibung
„grid-constant“
Entspricht „constant“*
„grid-mirror“
Entspricht „reflect“
„grid-wrap“
Entspricht „wrap“
* „grid-constant“ und „constant“ sind für Filteroperationen gleichwertig, haben aber unterschiedliches Verhalten bei Interpolationsfunktionen. Zur API-Konsistenz akzeptieren die Filterfunktionen beide Namen.
Der Modus „constant“ ist besonders, da er einen zusätzlichen Parameter benötigt, um den konstanten Wert anzugeben, der verwendet werden soll.
Beachten Sie, dass sich die Modi mirror und reflect nur darin unterscheiden, ob der Stichprobenwert am Rand bei der Reflexion wiederholt wird. Für den Modus mirror liegt der Symmetriepunkt genau am letzten Stichprobenwert, sodass dieser Wert nicht wiederholt wird. Dieser Modus wird auch als whole-sample symmetric bezeichnet, da der Symmetriepunkt auf dem letzten Stichprobenwert liegt. Ebenso wird reflect oft als half-sample symmetric bezeichnet, da der Symmetriepunkt eine halbe Stichprobe über den Array-Rand hinaus liegt.
Hinweis
Der einfachste Weg, solche Randbedingungen zu implementieren, wäre, die Daten in ein größeres Array zu kopieren und die Daten an den Rändern gemäß den Randbedingungen zu erweitern. Bei großen Arrays und großen Filterkernen wäre dies sehr speicherintensiv, und die unten beschriebenen Funktionen verwenden daher einen anderen Ansatz, der die Zuweisung großer temporärer Puffer nicht erfordert.
Korrelation und Faltung#
Die Funktion
correlate1dberechnet eine 1-D-Korrelation entlang der gegebenen Achse. Die Zeilen des Arrays entlang der gegebenen Achse werden mit den gegebenen weights korreliert. Der Parameter weights muss eine 1-D-Sequenz von Zahlen sein.Die Funktion
correlateimplementiert eine multidimensionale Korrelation des Eingabe-Arrays mit einem gegebenen Kern.Die Funktion
convolve1dberechnet eine 1-D-Faltung entlang der gegebenen Achse. Die Zeilen des Arrays entlang der gegebenen Achse werden mit den gegebenen weights gefaltet. Der Parameter weights muss eine 1-D-Sequenz von Zahlen sein.Die Funktion
convolveimplementiert eine multidimensionale Faltung des Eingabe-Arrays mit einem gegebenen Kern.Hinweis
Eine Faltung ist im Wesentlichen eine Korrelation nach Spiegelung des Kerns. Daher verhält sich der Parameter origin anders als bei einer Korrelation: das Ergebnis wird in die entgegengesetzte Richtung verschoben.
Glättungsfilter#
Die Funktion
gaussian_filter1dimplementiert einen 1-D-Gauß-Filter. Die Standardabweichung des Gauß-Filters wird über den Parameter sigma übergeben. Ein order = 0 entspricht der Faltung mit einem Gauß-Kern. Eine Ordnung von 1, 2 oder 3 entspricht der Faltung mit den ersten, zweiten oder dritten Ableitungen eines Gauß. Höhere Ableitungen sind nicht implementiert.Die Funktion
gaussian_filterimplementiert einen multidimensionalen Gauß-Filter. Die Standardabweichungen des Gauß-Filters entlang jeder Achse werden über den Parameter sigma als Sequenz oder Zahlen übergeben. Wenn sigma keine Sequenz, sondern eine einzelne Zahl ist, ist die Standardabweichung des Filters in allen Richtungen gleich. Die Ordnung des Filters kann für jede Achse separat angegeben werden. Eine Ordnung von 0 entspricht der Faltung mit einem Gauß-Kern. Eine Ordnung von 1, 2 oder 3 entspricht der Faltung mit der ersten, zweiten oder dritten Ableitung eines Gauß. Höhere Ableitungen sind nicht implementiert. Der Parameter order muss eine Zahl sein, um die gleiche Ordnung für alle Achsen anzugeben, oder eine Sequenz von Zahlen, um eine andere Ordnung für jede Achse anzugeben. Das folgende Beispiel zeigt die Anwendung des Filters auf Testdaten mit unterschiedlichen Werten von sigma. Der Parameter order bleibt bei 0.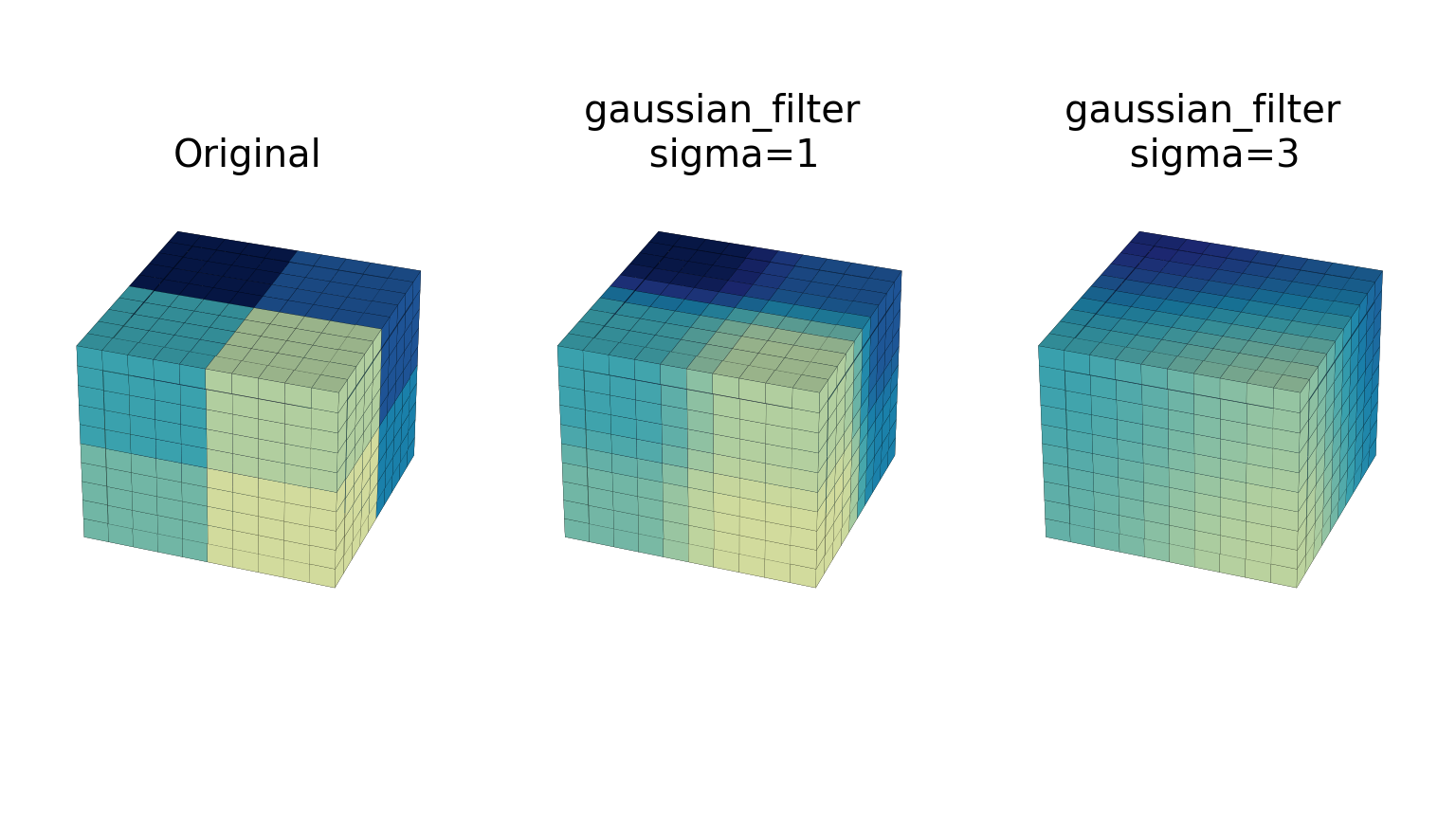
Hinweis
Der multidimensionale Filter wird als Sequenz von 1-D-Gauß-Filtern implementiert. Die Zwischen-Arrays werden im gleichen Datentyp wie die Ausgabe gespeichert. Daher können die Ergebnisse für Ausgabetypen mit geringerer Genauigkeit ungenau sein, da Zwischenergebnisse möglicherweise mit unzureichender Genauigkeit gespeichert werden. Dies kann durch Angabe eines genaueren Ausgabetypen verhindert werden.
Die Funktion
uniform_filter1dberechnet einen 1-D-Gleichverteilungsfilter der gegebenen size entlang der gegebenen Achse.Die Funktion
uniform_filterimplementiert einen multidimensionalen Gleichverteilungsfilter. Die Größen des Gleichverteilungsfilters werden für jede Achse als Sequenz von Ganzzahlen über den Parameter size angegeben. Wenn size keine Sequenz, sondern eine einzelne Zahl ist, wird angenommen, dass die Größen entlang aller Achsen gleich sind.Hinweis
Der multidimensionale Filter wird als Sequenz von 1-D-Gleichverteilungsfiltern implementiert. Die Zwischen-Arrays werden im gleichen Datentyp wie die Ausgabe gespeichert. Daher können die Ergebnisse für Ausgabetypen mit geringerer Genauigkeit ungenau sein, da Zwischenergebnisse möglicherweise mit unzureichender Genauigkeit gespeichert werden. Dies kann durch Angabe eines genaueren Ausgabetypen verhindert werden.
Filter basierend auf Ordnungsstatistiken#
Die Funktion
minimum_filter1dberechnet einen 1-D-Minimumfilter der gegebenen size entlang der gegebenen Achse.Die Funktion
maximum_filter1dberechnet einen 1-D-Maximumfilter der gegebenen size entlang der gegebenen Achse.Die Funktion
minimum_filterberechnet einen multidimensionalen Minimumfilter. Entweder die Größen eines rechteckigen Kerns oder der Fußabdruck des Kerns müssen angegeben werden. Der Parameter size muss, falls angegeben, eine Sequenz von Größen oder eine einzelne Zahl sein, in diesem Fall wird angenommen, dass die Größe des Filters entlang jeder Achse gleich ist. Der Parameter footprint muss, falls angegeben, ein Array sein, das die Form des Kerns durch seine Nicht-Null-Elemente definiert.Die Funktion
maximum_filterberechnet einen multidimensionalen Maximumfilter. Entweder die Größen eines rechteckigen Kerns oder der Fußabdruck des Kerns müssen angegeben werden. Der Parameter size muss, falls angegeben, eine Sequenz von Größen oder eine einzelne Zahl sein, in diesem Fall wird angenommen, dass die Größe des Filters entlang jeder Achse gleich ist. Der Parameter footprint muss, falls angegeben, ein Array sein, das die Form des Kerns durch seine Nicht-Null-Elemente definiert.Die Funktion
rank_filterberechnet einen multidimensionalen Rangfilter. Der rank kann kleiner als Null sein, d.h. rank = -1 bezeichnet das größte Element. Entweder die Größen eines rechteckigen Kerns oder der Fußabdruck des Kerns müssen angegeben werden. Der Parameter size muss, falls angegeben, eine Sequenz von Größen oder eine einzelne Zahl sein, in diesem Fall wird angenommen, dass die Größe des Filters entlang jeder Achse gleich ist. Der Parameter footprint muss, falls angegeben, ein Array sein, das die Form des Kerns durch seine Nicht-Null-Elemente definiert.Die Funktion
percentile_filterberechnet einen multidimensionalen Perzentilfilter. Das percentile kann kleiner als Null sein, d.h. percentile = -20 entspricht percentile = 80. Entweder die Größen eines rechteckigen Kerns oder der Fußabdruck des Kerns müssen angegeben werden. Der Parameter size muss, falls angegeben, eine Sequenz von Größen oder eine einzelne Zahl sein, in diesem Fall wird angenommen, dass die Größe des Filters entlang jeder Achse gleich ist. Der Parameter footprint muss, falls angegeben, ein Array sein, das die Form des Kerns durch seine Nicht-Null-Elemente definiert.Die Funktion
median_filterberechnet einen multidimensionalen Medianfilter. Entweder die Größen eines rechteckigen Kerns oder der Fußabdruck des Kerns müssen angegeben werden. Der Parameter size muss, falls angegeben, eine Sequenz von Größen oder eine einzelne Zahl sein, in diesem Fall wird angenommen, dass die Größe des Filters entlang jeder Achse gleich ist. Der Parameter footprint muss, falls angegeben, ein Array sein, das die Form des Kerns durch seine Nicht-Null-Elemente definiert.
Ableitungen#
Ableitungsfilter können auf verschiedene Weise konstruiert werden. Die Funktion gaussian_filter1d, die in Glättungsfilter beschrieben wird, kann zur Berechnung von Ableitungen entlang einer gegebenen Achse unter Verwendung des Parameters order verwendet werden. Andere Ableitungsfilter sind die Prewitt- und Sobel-Filter
Die Funktion
prewittberechnet eine Ableitung entlang der gegebenen Achse.Die Funktion
sobelberechnet eine Ableitung entlang der gegebenen Achse.
Der Laplace-Filter wird durch die Summe der zweiten Ableitungen entlang aller Achsen berechnet. Somit können verschiedene Laplace-Filter durch die Verwendung unterschiedlicher Zweitabteilungungsfunktionen konstruiert werden. Daher bieten wir eine allgemeine Funktion an, die ein Funktionsargument zur Berechnung der zweiten Ableitung in einer gegebenen Richtung aufnimmt.
Die Funktion
generic_laplaceberechnet einen Laplace-Filter unter Verwendung der überderivative2übergebenen Funktion zur Berechnung von zweiten Ableitungen. Die Funktionderivative2sollte die folgende Signatur habenderivative2(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)
Sie sollte die zweite Ableitung entlang der Dimension axis berechnen. Wenn output nicht
Noneist, sollte sie diese für die Ausgabe verwenden undNonezurückgeben, andernfalls sollte sie das Ergebnis zurückgeben. mode und cval haben die übliche Bedeutung.Die Argumente extra_arguments und extra_keywords können verwendet werden, um ein Tupel zusätzlicher Argumente und ein Dictionary benannter Argumente zu übergeben, die bei jedem Aufruf an
derivative2übergeben werden.Zum Beispiel
>>> def d2(input, axis, output, mode, cval): ... return correlate1d(input, [1, -2, 1], axis, output, mode, cval, 0) ... >>> a = np.zeros((5, 5)) >>> a[2, 2] = 1 >>> from scipy.ndimage import generic_laplace >>> generic_laplace(a, d2) array([[ 0., 0., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [ 0., 1., -4., 1., 0.], [ 0., 0., 1., 0., 0.], [ 0., 0., 0., 0., 0.]])
Um die Verwendung des Arguments extra_arguments zu demonstrieren, könnten wir Folgendes tun
>>> def d2(input, axis, output, mode, cval, weights): ... return correlate1d(input, weights, axis, output, mode, cval, 0,) ... >>> a = np.zeros((5, 5)) >>> a[2, 2] = 1 >>> generic_laplace(a, d2, extra_arguments = ([1, -2, 1],)) array([[ 0., 0., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [ 0., 1., -4., 1., 0.], [ 0., 0., 1., 0., 0.], [ 0., 0., 0., 0., 0.]])
oder
>>> generic_laplace(a, d2, extra_keywords = {'weights': [1, -2, 1]}) array([[ 0., 0., 0., 0., 0.], [ 0., 0., 1., 0., 0.], [ 0., 1., -4., 1., 0.], [ 0., 0., 1., 0., 0.], [ 0., 0., 0., 0., 0.]])
Die folgenden beiden Funktionen werden mit generic_laplace implementiert, indem geeignete Funktionen für die Zweitableitungsfunktion bereitgestellt werden
Die Funktion
laplaceberechnet den Laplace unter Verwendung diskreter Differenzierung für die zweite Ableitung (d.h. Faltung mit[1, -2, 1]).Die Funktion
gaussian_laplaceberechnet den Laplace-Filter unter Verwendung vongaussian_filterzur Berechnung der zweiten Ableitungen. Die Standardabweichungen des Gauß-Filters entlang jeder Achse werden über den Parameter sigma als Sequenz oder Zahlen übergeben. Wenn sigma keine Sequenz, sondern eine einzelne Zahl ist, ist die Standardabweichung des Filters in allen Richtungen gleich.
Die Gradientenmagnitude ist definiert als die Quadratwurzel der Summe der Quadrate der Gradienten in allen Richtungen. Ähnlich wie bei der allgemeinen Laplace-Funktion gibt es eine Funktion generic_gradient_magnitude, die die Gradientenmagnitude eines Arrays berechnet.
Die Funktion
generic_gradient_magnitudeberechnet eine Gradientenmagnitude unter Verwendung der überderivativeübergebenen Funktion zur Berechnung erster Ableitungen. Die Funktionderivativesollte die folgende Signatur habenderivative(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)
Sie sollte die Ableitung entlang der Dimension axis berechnen. Wenn output nicht
Noneist, sollte sie diese für die Ausgabe verwenden undNonezurückgeben, andernfalls sollte sie das Ergebnis zurückgeben. mode und cval haben die übliche Bedeutung.Die Argumente extra_arguments und extra_keywords können verwendet werden, um ein Tupel zusätzlicher Argumente und ein Dictionary benannter Argumente zu übergeben, die bei jedem Aufruf an derivative übergeben werden.
Zum Beispiel passt die Funktion
sobelzur erforderlichen Signatur>>> a = np.zeros((5, 5)) >>> a[2, 2] = 1 >>> from scipy.ndimage import sobel, generic_gradient_magnitude >>> generic_gradient_magnitude(a, sobel) array([[ 0. , 0. , 0. , 0. , 0. ], [ 0. , 1.41421356, 2. , 1.41421356, 0. ], [ 0. , 2. , 0. , 2. , 0. ], [ 0. , 1.41421356, 2. , 1.41421356, 0. ], [ 0. , 0. , 0. , 0. , 0. ]])
Siehe die Dokumentation von
generic_laplacefür Beispiele zur Verwendung der Argumente extra_arguments und extra_keywords.
Die Funktionen sobel und prewitt passen zur erforderlichen Signatur und können daher direkt mit generic_gradient_magnitude verwendet werden.
Die Funktion
gaussian_gradient_magnitudeberechnet die Gradientenmagnitude unter Verwendung vongaussian_filterzur Berechnung der ersten Ableitungen. Die Standardabweichungen des Gauß-Filters entlang jeder Achse werden über den Parameter sigma als Sequenz oder Zahlen übergeben. Wenn sigma keine Sequenz, sondern eine einzelne Zahl ist, ist die Standardabweichung des Filters in allen Richtungen gleich.
Generische Filterfunktionen#
Zur Implementierung von Filterfunktionen können generische Funktionen verwendet werden, die ein aufrufbares Objekt akzeptieren, das die Filteroperation implementiert. Die Iteration über die Eingabe- und Ausgabearrays wird von diesen generischen Funktionen übernommen, zusammen mit Details wie der Implementierung der Randbedingungen. Nur ein aufrufbares Objekt, das eine Callback-Funktion implementiert, die die eigentliche Filterarbeit leistet, muss bereitgestellt werden. Die Callback-Funktion kann auch in C geschrieben und über eine PyCapsule übergeben werden (siehe Erweiterung von scipy.ndimage in C für weitere Informationen).
Die Funktion
generic_filter1dimplementiert eine generische 1-D-Filterfunktion, wobei die eigentliche Filteroperation als Python-Funktion (oder ein anderes aufrufbares Objekt) bereitgestellt werden muss. Die Funktiongeneric_filter1diteriert über die Zeilen eines Arrays und ruftfunctionfür jede Zeile auf. Die Argumente, die anfunctionübergeben werden, sind 1-D-Arrays vom Typnumpy.float64. Das erste enthält die Werte der aktuellen Zeile. Es wird am Anfang und Ende erweitert, gemäß den Argumenten filter_size und origin. Das zweite Array sollte direkt modifiziert werden, um die Ausgabewerte der Zeile bereitzustellen. Betrachten wir zum Beispiel eine Korrelation entlang einer Dimension>>> a = np.arange(12).reshape(3,4) >>> correlate1d(a, [1, 2, 3]) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
Die gleiche Operation kann auch mit
generic_filter1dimplementiert werden, wie folgt>>> def fnc(iline, oline): ... oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:] ... >>> from scipy.ndimage import generic_filter1d >>> generic_filter1d(a, fnc, 3) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
Hier wurde der Ursprung des Kerns (standardmäßig) in der Mitte des Filters der Länge 3 angenommen. Daher wurde jede Eingabezeile am Anfang und Ende um einen Wert erweitert, bevor die Funktion aufgerufen wurde.
Optional können zusätzliche Argumente definiert und an die Filterfunktion übergeben werden. Die Argumente extra_arguments und extra_keywords können verwendet werden, um ein Tupel zusätzlicher Argumente und/oder ein Dictionary benannter Argumente zu übergeben, die bei jedem Aufruf an derivative übergeben werden. Zum Beispiel können wir die Parameter unseres Filters als Argument übergeben
>>> def fnc(iline, oline, a, b): ... oline[...] = iline[:-2] + a * iline[1:-1] + b * iline[2:] ... >>> generic_filter1d(a, fnc, 3, extra_arguments = (2, 3)) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
oder
>>> generic_filter1d(a, fnc, 3, extra_keywords = {'a':2, 'b':3}) array([[ 3, 8, 14, 17], [27, 32, 38, 41], [51, 56, 62, 65]])
Die Funktion
generic_filterimplementiert eine generische Filterfunktion, bei der die eigentliche Filteroperation als Python-Funktion (oder ein anderes aufrufbares Objekt) bereitgestellt werden muss. Die Funktiongeneric_filteriteriert über das Array und ruftfunctionfür jedes Element auf. Das Argument vonfunctionist ein 1-D-Array vom Typnumpy.float64, das die Werte um das aktuelle Element enthält, die sich innerhalb des Fußabdrucks des Filters befinden. Die Funktion sollte einen einzelnen Wert zurückgeben, der in eine doppelt genaue Zahl konvertiert werden kann. Betrachten wir zum Beispiel eine Korrelation>>> a = np.arange(12).reshape(3,4) >>> correlate(a, [[1, 0], [0, 3]]) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
Die gleiche Operation kann auch mit generic_filter wie folgt implementiert werden
>>> def fnc(buffer): ... return (buffer * np.array([1, 3])).sum() ... >>> from scipy.ndimage import generic_filter >>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]]) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
Hier wurde ein Kern-Fußabdruck angegeben, der nur zwei Elemente enthält. Daher erhält die Filterfunktion einen Puffer der Länge zwei, der mit den entsprechenden Gewichten multipliziert und die Summe gebildet wurde.
Beim Aufruf von
generic_filtermüssen entweder die Größen eines rechteckigen Kerns oder der Fußabdruck des Kerns angegeben werden. Der Parameter size muss, falls angegeben, eine Sequenz von Größen oder eine einzelne Zahl sein, in diesem Fall wird angenommen, dass die Größe des Filters entlang jeder Achse gleich ist. Der Parameter footprint muss, falls angegeben, ein Array sein, das die Form des Kerns durch seine Nicht-Null-Elemente definiert.Optional können zusätzliche Argumente definiert und an die Filterfunktion übergeben werden. Die Argumente extra_arguments und extra_keywords können verwendet werden, um ein Tupel zusätzlicher Argumente und/oder ein Dictionary benannter Argumente zu übergeben, die bei jedem Aufruf an derivative übergeben werden. Zum Beispiel können wir die Parameter unseres Filters als Argument übergeben
>>> def fnc(buffer, weights): ... weights = np.asarray(weights) ... return (buffer * weights).sum() ... >>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_arguments = ([1, 3],)) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
oder
>>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_keywords= {'weights': [1, 3]}) array([[ 0, 3, 7, 11], [12, 15, 19, 23], [28, 31, 35, 39]])
Diese Funktionen iterieren über die Zeilen oder Elemente beginnend mit der letzten Achse, d.h. der letzte Index ändert sich am schnellsten. Diese Iterationsreihenfolge ist für den Fall garantiert, dass es wichtig ist, den Filter je nach räumlicher Position anzupassen. Hier ist ein Beispiel für die Verwendung einer Klasse, die den Filter implementiert und die aktuellen Koordinaten während der Iteration verfolgt. Sie führt die gleiche Filteroperation aus wie oben für generic_filter beschrieben, gibt aber zusätzlich die aktuellen Koordinaten aus
>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc_class:
... def __init__(self, shape):
... # store the shape:
... self.shape = shape
... # initialize the coordinates:
... self.coordinates = [0] * len(shape)
...
... def filter(self, buffer):
... result = (buffer * np.array([1, 3])).sum()
... print(self.coordinates)
... # calculate the next coordinates:
... axes = list(range(len(self.shape)))
... axes.reverse()
... for jj in axes:
... if self.coordinates[jj] < self.shape[jj] - 1:
... self.coordinates[jj] += 1
... break
... else:
... self.coordinates[jj] = 0
... return result
...
>>> fnc = fnc_class(shape = (3,4))
>>> generic_filter(a, fnc.filter, footprint = [[1, 0], [0, 1]])
[0, 0]
[0, 1]
[0, 2]
[0, 3]
[1, 0]
[1, 1]
[1, 2]
[1, 3]
[2, 0]
[2, 1]
[2, 2]
[2, 3]
array([[ 0, 3, 7, 11],
[12, 15, 19, 23],
[28, 31, 35, 39]])
Für die Funktion generic_filter1d funktioniert der gleiche Ansatz, nur dass diese Funktion nicht über die gefilterte Achse iteriert. Das Beispiel für generic_filter1d sieht dann so aus
>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc1d_class:
... def __init__(self, shape, axis = -1):
... # store the filter axis:
... self.axis = axis
... # store the shape:
... self.shape = shape
... # initialize the coordinates:
... self.coordinates = [0] * len(shape)
...
... def filter(self, iline, oline):
... oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
... print(self.coordinates)
... # calculate the next coordinates:
... axes = list(range(len(self.shape)))
... # skip the filter axis:
... del axes[self.axis]
... axes.reverse()
... for jj in axes:
... if self.coordinates[jj] < self.shape[jj] - 1:
... self.coordinates[jj] += 1
... break
... else:
... self.coordinates[jj] = 0
...
>>> fnc = fnc1d_class(shape = (3,4))
>>> generic_filter1d(a, fnc.filter, 3)
[0, 0]
[1, 0]
[2, 0]
array([[ 3, 8, 14, 17],
[27, 32, 38, 41],
[51, 56, 62, 65]])
Fourier-Domänen-Filter#
Die in diesem Abschnitt beschriebenen Funktionen führen Filteroperationen im Fourier-Raum durch. Daher sollte das Eingabearray einer solchen Funktion mit einer inversen Fourier-Transformationsfunktion kompatibel sein, wie z. B. den Funktionen aus dem Modul numpy.fft. Wir haben es daher mit Arrays zu tun, die das Ergebnis einer realen oder komplexen Fourier-Transformation sein können. Bei einer realen Fourier-Transformation wird nur die Hälfte der symmetrischen komplexen Transformation gespeichert. Zusätzlich muss bekannt sein, wie lang die Achse war, die durch die reelle FFT transformiert wurde. Die hier beschriebenen Funktionen bieten einen Parameter n, der im Falle einer reellen Transformation gleich der Länge der reellen Transformationsachse vor der Transformation sein muss. Ist dieser Parameter kleiner als Null, wird angenommen, dass das Eingabearray das Ergebnis einer komplexen Fourier-Transformation war. Der Parameter axis kann verwendet werden, um anzugeben, entlang welcher Achse die reelle Transformation ausgeführt wurde.
Die Funktion
fourier_shiftmultipliziert das Eingabearray mit der mehrdimensionalen Fourier-Transformation einer Verschiebungsoperation für die gegebene Verschiebung. Der Parameter shift ist eine Sequenz von Verschiebungen für jede Dimension oder ein einzelner Wert für alle Dimensionen.Die Funktion
fourier_gaussianmultipliziert das Eingabearray mit der mehrdimensionalen Fourier-Transformation eines Gauß-Filters mit den gegebenen Standardabweichungen sigma. Der Parameter sigma ist eine Sequenz von Werten für jede Dimension oder ein einzelner Wert für alle Dimensionen.Die Funktion
fourier_uniformmultipliziert das Eingabearray mit der mehrdimensionalen Fourier-Transformation eines Gleichverteilungsfilters mit den gegebenen Größen size. Der Parameter size ist eine Sequenz von Werten für jede Dimension oder ein einzelner Wert für alle Dimensionen.Die Funktion
fourier_ellipsoidmultipliziert das Eingabearray mit der mehrdimensionalen Fourier-Transformation eines elliptisch geformten Filters mit den gegebenen Größen size. Der Parameter size ist eine Sequenz von Werten für jede Dimension oder ein einzelner Wert für alle Dimensionen. Diese Funktion ist nur für die Dimensionen 1, 2 und 3 implementiert.
Interpolationsfunktionen#
Dieser Abschnitt beschreibt verschiedene Interpolationsfunktionen, die auf der B-Spline-Theorie basieren. Eine gute Einführung in B-Splines findet sich in [1], mit detaillierten Algorithmen für die Bildinterpolation in [5].
Spline-Vorfilter#
Die Interpolation mit Splines höherer Ordnung als 1 erfordert einen Vorfilterschritt. Die in Abschnitt Interpolationsfunktionen beschriebenen Interpolationsfunktionen führen eine Vorfilterung durch, indem sie spline_filter aufrufen, können aber angewiesen werden, dies nicht zu tun, indem das Schlüsselwort prefilter auf False gesetzt wird. Dies ist nützlich, wenn mehr als eine Interpolationsoperation auf demselben Array durchgeführt wird. In diesem Fall ist es effizienter, die Vorfilterung nur einmal durchzuführen und ein vor-gefiltertes Array als Eingabe für die Interpolationsfunktionen zu verwenden. Die folgenden beiden Funktionen implementieren die Vorfilterung.
Die Funktion
spline_filter1dberechnet einen 1-D-Spline-Filter entlang der gegebenen Achse. Optional kann ein Ausgabearray bereitgestellt werden. Die Ordnung des Splines muss größer als 1 und kleiner als 6 sein.Die Funktion
spline_filterberechnet einen mehrdimensionalen Spline-Filter.Hinweis
Der mehrdimensionale Filter wird als eine Sequenz von 1-D-Spline-Filtern implementiert. Die Zwischenarrays werden im selben Datentyp wie die Ausgabe gespeichert. Daher können die Ergebnisse ungenau sein, wenn eine Ausgabe mit begrenzter Genauigkeit angefordert wird, da Zwischenergebnisse möglicherweise mit unzureichender Genauigkeit gespeichert werden. Dies kann verhindert werden, indem ein Ausgabetyp mit hoher Genauigkeit angegeben wird.
Randbehandlung bei der Interpolation#
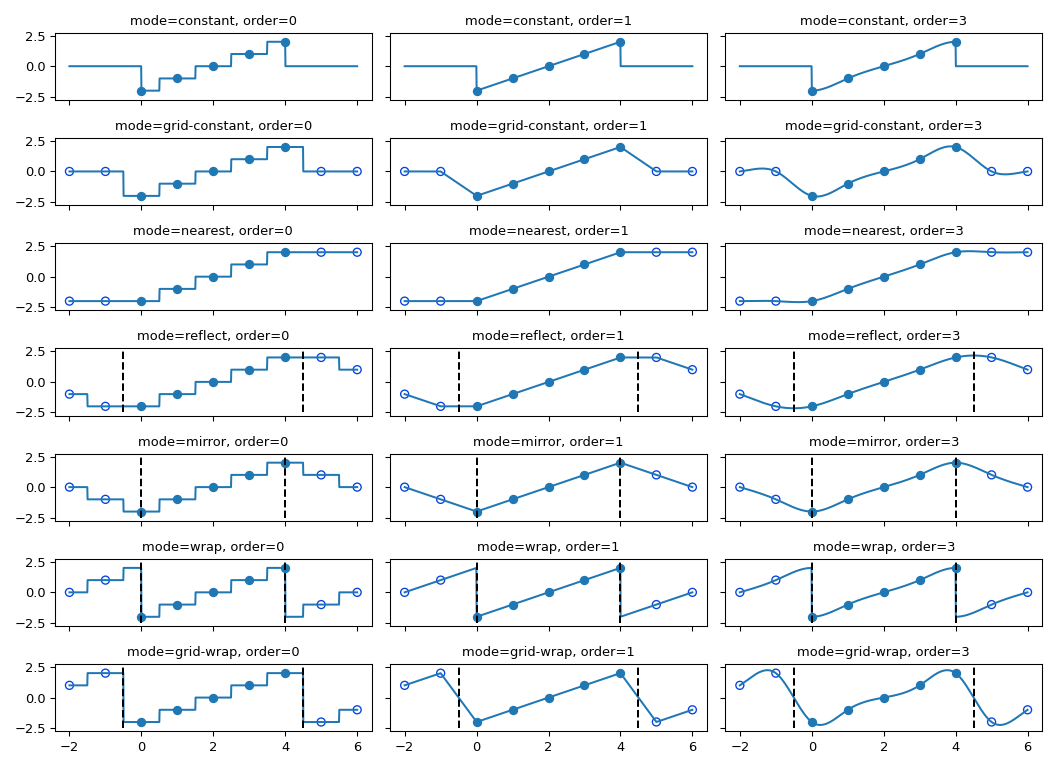
Die Interpolationsfunktionen verwenden alle Spline-Interpolation, um eine Art geometrische Transformation des Eingabearrays zu bewirken. Dies erfordert eine Abbildung der Ausgabekoordinaten auf die Eingabekoordinaten, und daher kann die Möglichkeit entstehen, dass Eingabewerte außerhalb der Grenzen benötigt werden. Dieses Problem wird auf die gleiche Weise gelöst wie in Filterfunktionen für die mehrdimensionalen Filterfunktionen beschrieben. Daher unterstützen alle diese Funktionen einen Parameter mode, der bestimmt, wie die Ränder behandelt werden, und einen Parameter cval, der einen konstanten Wert angibt, falls der Modus 'constant' verwendet wird. Das Verhalten aller Modi, auch an nicht-ganzzahligen Stellen, wird unten veranschaulicht. Beachten Sie, dass die Ränder nicht bei allen Modi gleich behandelt werden; reflect (auch bekannt als grid-mirror) und grid-wrap beinhalten Symmetrie oder Wiederholung um einen Punkt, der sich auf halbem Weg zwischen Bildabtastwerten befindet (gestrichelte vertikale Linien), während die Modi mirror und wrap das Bild so behandeln, als ob seine Ausdehnung genau am ersten und letzten Abtastpunkt endet, anstatt 0,5 Abtastwerte darüber hinaus.
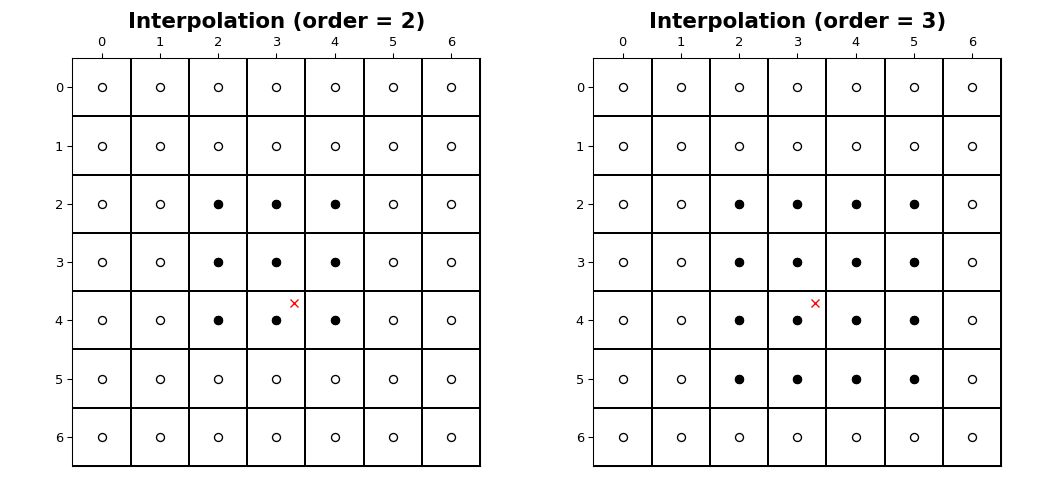
Die Koordinaten der Bildabtastwerte liegen auf ganzzahligen Abtastpositionen im Bereich von 0 bis shape[i] - 1 entlang jeder Achse i. Die folgende Abbildung veranschaulicht die Interpolation eines Punkts an der Position (3.7, 3.3) innerhalb eines Bildes der Form (7, 7). Für eine Interpolation der Ordnung n werden entlang jeder Achse n + 1 Abtastwerte verwendet. Die gefüllten Kreise veranschaulichen die Abtastpositionen, die für die Interpolation des Wertes an der Position des roten X verwendet werden.
Interpolationsfunktionen#
Die Funktion
geometric_transformwendet eine beliebige geometrische Transformation auf die Eingabe an. Die angegebene mapping-Funktion wird an jedem Punkt der Ausgabe aufgerufen, um die entsprechenden Koordinaten in der Eingabe zu finden. mapping muss ein aufrufbares Objekt sein, das ein Tupel der Länge gleich dem Rang des Ausgabearrays akzeptiert und die entsprechenden Eingabekoordinaten als Tupel der Länge gleich dem Rang des Eingabearrays zurückgibt. Die Ausgabegröße und der Ausgabetyp können optional angegeben werden. Wenn sie nicht angegeben werden, sind sie gleich der Eingabegröße und dem Eingabetyp.Zum Beispiel
>>> a = np.arange(12).reshape(4,3).astype(np.float64) >>> def shift_func(output_coordinates): ... return (output_coordinates[0] - 0.5, output_coordinates[1] - 0.5) ... >>> from scipy.ndimage import geometric_transform >>> geometric_transform(a, shift_func) array([[ 0. , 0. , 0. ], [ 0. , 1.3625, 2.7375], [ 0. , 4.8125, 6.1875], [ 0. , 8.2625, 9.6375]])
Optional können zusätzliche Argumente definiert und an die Filterfunktion übergeben werden. Die Argumente extra_arguments und extra_keywords können verwendet werden, um ein Tupel zusätzlicher Argumente und/oder ein Wörterbuch benannter Argumente zu übergeben, die bei jedem Aufruf an die Ableitung weitergegeben werden. Zum Beispiel können wir die Verschiebungen in unserem Beispiel als Argumente übergeben.
>>> def shift_func(output_coordinates, s0, s1): ... return (output_coordinates[0] - s0, output_coordinates[1] - s1) ... >>> geometric_transform(a, shift_func, extra_arguments = (0.5, 0.5)) array([[ 0. , 0. , 0. ], [ 0. , 1.3625, 2.7375], [ 0. , 4.8125, 6.1875], [ 0. , 8.2625, 9.6375]])
oder
>>> geometric_transform(a, shift_func, extra_keywords = {'s0': 0.5, 's1': 0.5}) array([[ 0. , 0. , 0. ], [ 0. , 1.3625, 2.7375], [ 0. , 4.8125, 6.1875], [ 0. , 8.2625, 9.6375]])
Hinweis
Die Mapping-Funktion kann auch in C geschrieben und über ein
scipy.LowLevelCallableübergeben werden. Weitere Informationen finden Sie unter Erweiterung von scipy.ndimage in C.Die Funktion
map_coordinateswendet eine beliebige Koordinatentransformation mithilfe des gegebenen Koordinatenarrays an. Die Form der Ausgabe wird aus der des Koordinatenarrays abgeleitet, indem die erste Achse weggelassen wird. Der Parameter coordinates wird verwendet, um für jeden Punkt in der Ausgabe die entsprechenden Koordinaten in der Eingabe zu finden. Die Werte von coordinates entlang der ersten Achse sind die Koordinaten im Eingabearray, an denen der Ausgabewert gefunden wird. (Siehe auch die Funktion coordinates in numarray.) Da die Koordinaten nicht-ganzzahlige Koordinaten sein können, wird der Wert der Eingabe an diesen Koordinaten durch Spline-Interpolation der angeforderten Ordnung bestimmt.Hier ist ein Beispiel für die Interpolation eines 2D-Arrays an
(0.5, 0.5)und(1, 2).>>> a = np.arange(12).reshape(4,3).astype(np.float64) >>> a array([[ 0., 1., 2.], [ 3., 4., 5.], [ 6., 7., 8.], [ 9., 10., 11.]]) >>> from scipy.ndimage import map_coordinates >>> map_coordinates(a, [[0.5, 2], [0.5, 1]]) array([ 1.3625, 7.])
Die Funktion
affine_transformwendet eine affine Transformation auf das Eingabearray an. Die angegebene Transformationsmatrix und der offset werden verwendet, um für jeden Punkt in der Ausgabe die entsprechenden Koordinaten in der Eingabe zu finden. Der Wert der Eingabe an den berechneten Koordinaten wird durch Spline-Interpolation der angeforderten Ordnung bestimmt. Die Transformationsmatrix muss 2D sein oder kann auch als 1D-Sequenz oder Array angegeben werden. Im letzteren Fall wird angenommen, dass die Matrix diagonal ist. Dann wird ein effizienterer Interpolationsalgorithmus angewendet, der die Trennbarkeit des Problems ausnutzt. Die Ausgabegröße und der Ausgabetyp können optional angegeben werden. Wenn sie nicht angegeben werden, sind sie gleich der Eingabegröße und dem Eingabetyp.Die Funktion
shiftgibt eine verschobene Version der Eingabe zurück, wobei Spline-Interpolation der angeforderten order verwendet wird.Die Funktion
zoomgibt eine skalierte Version der Eingabe zurück, wobei Spline-Interpolation der angeforderten order verwendet wird.Die Funktion
rotategibt das Eingabearray zurück, das in der durch die beiden durch den Parameter axes gegebenen Achsen definierten Ebene gedreht ist, wobei Spline-Interpolation der angeforderten order verwendet wird. Der Winkel muss in Grad angegeben werden. Wenn reshape wahr ist, wird die Größe des Ausgabearrays angepasst, um die gedrehte Eingabe zu enthalten.
Morphologie#
Binäre Morphologie#
Die Funktion
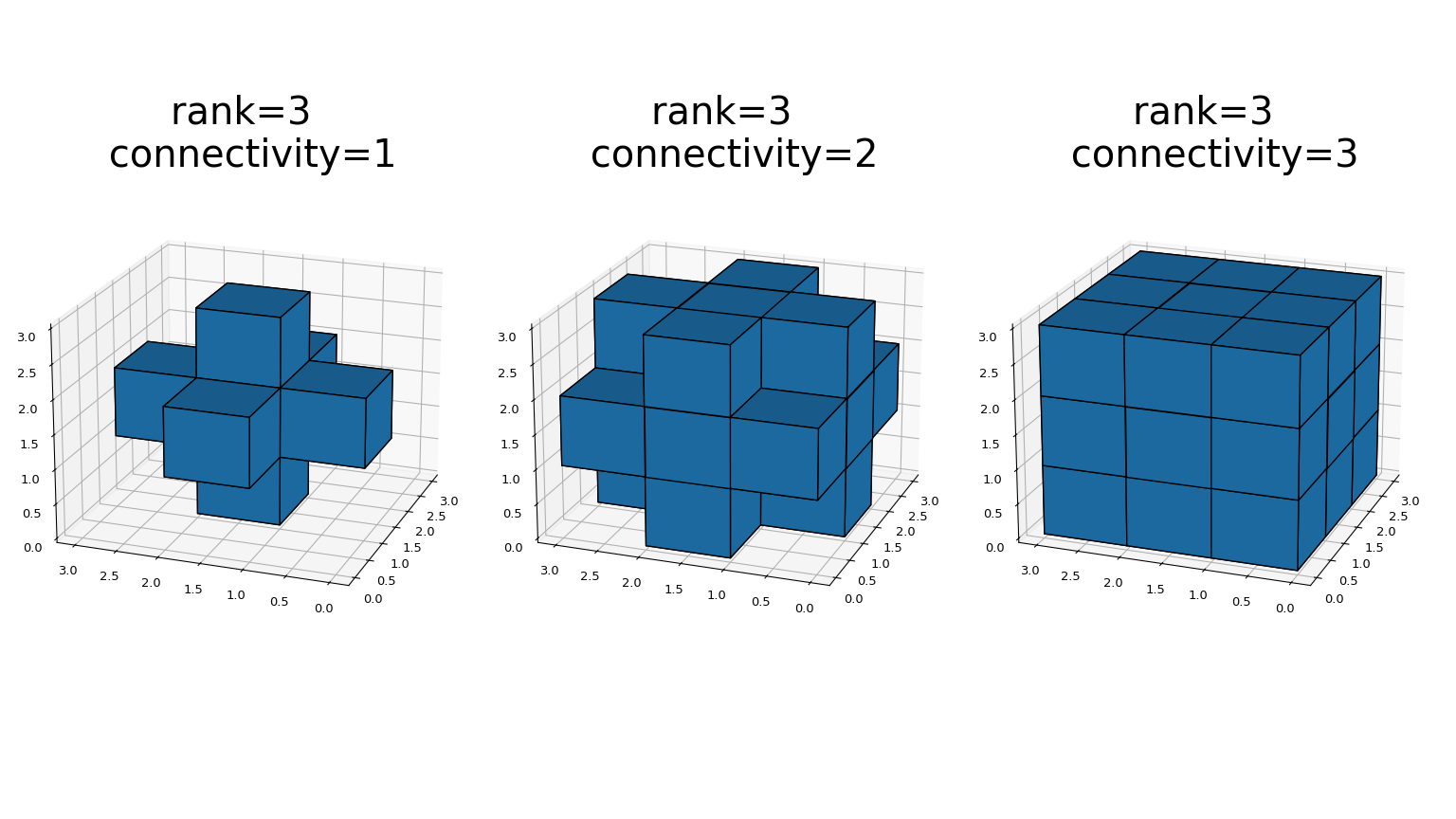
generate_binary_structuregeneriert ein binäres Strukturierungselement für die Verwendung in binären Morphologieoperationen. Der rank der Struktur muss angegeben werden. Die Größe der zurückgegebenen Struktur ist in jeder Richtung gleich drei. Der Wert jedes Elements ist gleich eins, wenn das Quadrat des Euklidischen Abstands vom Element zum Zentrum kleiner oder gleich connectivity ist. Zum Beispiel werden 2D-4-fach und 8-fach verbundene Strukturen wie folgt erzeugt.>>> from scipy.ndimage import generate_binary_structure >>> generate_binary_structure(2, 1) array([[False, True, False], [ True, True, True], [False, True, False]], dtype=bool) >>> generate_binary_structure(2, 2) array([[ True, True, True], [ True, True, True], [ True, True, True]], dtype=bool)
Dies ist eine visuelle Darstellung von generate_binary_structure in 3D.
Die meisten binären Morphologiefunktionen können durch die grundlegenden Operationen Erosion und Dilatation ausgedrückt werden, die hier zu sehen sind.
Die Funktion
binary_erosionimplementiert die binäre Erosion von Arrays beliebigen Rangs mit dem gegebenen Strukturierungselement. Der Parameter origin steuert die Platzierung des Strukturierungselements, wie in Filterfunktionen beschrieben. Wenn kein Strukturierungselement bereitgestellt wird, wird ein Element mit einer Konnektivität von eins mithilfe vongenerate_binary_structuregeneriert. Der Parameter border_value gibt den Wert des Arrays außerhalb der Grenzen an. Die Erosion wird iterations mal wiederholt. Wenn iterations kleiner als eins ist, wird die Erosion wiederholt, bis sich das Ergebnis nicht mehr ändert. Wenn ein mask-Array angegeben wird, werden nur die Elemente geändert, die an der entsprechenden Maskenelement einen wahren Wert haben, bei jeder Iteration.Die Funktion
binary_dilationimplementiert die binäre Dilatation von Arrays beliebigen Rangs mit dem gegebenen Strukturierungselement. Der Parameter origin steuert die Platzierung des Strukturierungselements, wie in Filterfunktionen beschrieben. Wenn kein Strukturierungselement bereitgestellt wird, wird ein Element mit einer Konnektivität von eins mithilfe vongenerate_binary_structuregeneriert. Der Parameter border_value gibt den Wert des Arrays außerhalb der Grenzen an. Die Dilatation wird iterations mal wiederholt. Wenn iterations kleiner als eins ist, wird die Dilatation wiederholt, bis sich das Ergebnis nicht mehr ändert. Wenn ein mask-Array angegeben wird, werden nur die Elemente geändert, die an der entsprechenden Maskenelement einen wahren Wert haben, bei jeder Iteration.
Hier ist ein Beispiel für die Verwendung von binary_dilation, um alle Elemente zu finden, die den Rand berühren, indem ein leeres Array vom Rand aus wiederholt dilatiert wird, wobei das Datenarray als Maske verwendet wird.
>>> struct = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> a = np.array([[1,0,0,0,0], [1,1,0,1,0], [0,0,1,1,0], [0,0,0,0,0]])
>>> a
array([[1, 0, 0, 0, 0],
[1, 1, 0, 1, 0],
[0, 0, 1, 1, 0],
[0, 0, 0, 0, 0]])
>>> from scipy.ndimage import binary_dilation
>>> binary_dilation(np.zeros(a.shape), struct, -1, a, border_value=1)
array([[ True, False, False, False, False],
[ True, True, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False]], dtype=bool)
Die Funktionen binary_erosion und binary_dilation haben beide einen Parameter iterations, der es ermöglicht, die Erosion oder Dilatation mehrmals zu wiederholen. Eine Erosion oder Dilatation mit einer Struktur n mal zu wiederholen, ist gleichbedeutend mit einer Erosion oder Dilatation mit einer Struktur, die n-1 mal mit sich selbst dilatiert wurde. Eine Funktion wird bereitgestellt, die die Berechnung einer Struktur ermöglicht, die mehrmals mit sich selbst dilatiert wurde.
Die Funktion
iterate_structuregibt eine Struktur zurück, indem die Eingabestruktur iteration - 1 Mal mit sich selbst dilatiert wird.Zum Beispiel.
>>> struct = generate_binary_structure(2, 1) >>> struct array([[False, True, False], [ True, True, True], [False, True, False]], dtype=bool) >>> from scipy.ndimage import iterate_structure >>> iterate_structure(struct, 2) array([[False, False, True, False, False], [False, True, True, True, False], [ True, True, True, True, True], [False, True, True, True, False], [False, False, True, False, False]], dtype=bool) If the origin of the original structure is equal to 0, then it is also equal to 0 for the iterated structure. If not, the origin must also be adapted if the equivalent of the *iterations* erosions or dilations must be achieved with the iterated structure. The adapted origin is simply obtained by multiplying with the number of iterations. For convenience, the :func:`iterate_structure` also returns the adapted origin if the *origin* parameter is not ``None``: .. code:: python >>> iterate_structure(struct, 2, -1) (array([[False, False, True, False, False], [False, True, True, True, False], [ True, True, True, True, True], [False, True, True, True, False], [False, False, True, False, False]], dtype=bool), [-2, -2])
Andere Morphologieoperationen können in Bezug auf Erosion und Dilatation definiert werden. Die folgenden Funktionen bieten einige dieser Operationen zur Bequemlichkeit.
Die Funktion
binary_openingimplementiert die binäre Öffnung von Arrays beliebigen Rangs mit dem gegebenen Strukturierungselement. Die binäre Öffnung ist gleichbedeutend mit einer binären Erosion, gefolgt von einer binären Dilatation mit demselben Strukturierungselement. Der Parameter origin steuert die Platzierung des Strukturierungselements, wie in Filterfunktionen beschrieben. Wenn kein Strukturierungselement bereitgestellt wird, wird ein Element mit einer Konnektivität von eins mithilfe vongenerate_binary_structuregeneriert. Der Parameter iterations gibt die Anzahl der durchgeführten Erosionen an, gefolgt von der gleichen Anzahl von Dilatationen.Die Funktion
binary_closingimplementiert die binäre Schließung von Arrays beliebigen Rangs mit dem gegebenen Strukturierungselement. Die binäre Schließung ist gleichbedeutend mit einer binären Dilatation, gefolgt von einer binären Erosion mit demselben Strukturierungselement. Der Parameter origin steuert die Platzierung des Strukturierungselements, wie in Filterfunktionen beschrieben. Wenn kein Strukturierungselement bereitgestellt wird, wird ein Element mit einer Konnektivität von eins mithilfe vongenerate_binary_structuregeneriert. Der Parameter iterations gibt die Anzahl der durchgeführten Dilatationen an, gefolgt von der gleichen Anzahl von Erosionen.Die Funktion
binary_fill_holeswird verwendet, um Löcher in Objekten eines binären Bildes zu schließen, wobei die Struktur die Konnektivität der Löcher definiert. Der Parameter origin steuert die Platzierung des Strukturierungselements, wie in Filterfunktionen beschrieben. Wenn kein Strukturierungselement bereitgestellt wird, wird ein Element mit einer Konnektivität von eins mithilfe vongenerate_binary_structuregeneriert.Die Funktion
binary_hit_or_missimplementiert eine binäre Hit-or-Miss-Transformation von Arrays beliebigen Rangs mit den gegebenen Strukturierungselementen. Die Hit-or-Miss-Transformation wird berechnet durch Erosion der Eingabe mit der ersten Struktur, Erosion des logischen nicht der Eingabe mit der zweiten Struktur, gefolgt vom logischen und dieser beiden Erosionen. Die origin-Parameter steuern die Platzierung der Strukturierungselemente, wie in Filterfunktionen beschrieben. Wenn origin2 gleichNoneist, wird es gleich dem Parameter origin1 gesetzt. Wenn das erste Strukturierungselement nicht bereitgestellt wird, wird ein Strukturierungselement mit einer Konnektivität von eins mithilfe vongenerate_binary_structuregeneriert. Wenn structure2 nicht bereitgestellt wird, wird es gleich dem logischen nicht von structure1 gesetzt.
Graustufenmorphologie#
Graustufenmorphologieoperationen sind die Äquivalente von binären Morphologieoperationen, die auf Arrays mit beliebigen Werten arbeiten. Im Folgenden beschreiben wir die Graustufen-Äquivalente von Erosion, Dilatation, Öffnung und Schließung. Diese Operationen werden auf ähnliche Weise implementiert wie die in Filterfunktionen beschriebenen Filter, und wir verweisen auf diesen Abschnitt für die Beschreibung von Kerneln und Footprints sowie die Behandlung von Array-Rändern. Die Graustufenmorphologieoperationen nehmen optional einen Parameter structure entgegen, der die Werte des Strukturierungselements angibt. Wenn dieser Parameter nicht angegeben wird, wird angenommen, dass das Strukturierungselement flach mit einem Wert von Null ist. Die Form der Struktur kann optional durch den Parameter footprint definiert werden. Wenn dieser Parameter nicht angegeben wird, wird angenommen, dass die Struktur rechteckig ist, mit Größen, die den Dimensionen des structure-Arrays entsprechen, oder durch den Parameter size, wenn structure nicht angegeben ist. Der Parameter size wird nur verwendet, wenn sowohl structure als auch footprint nicht angegeben sind. In diesem Fall wird angenommen, dass das Strukturierungselement rechteckig und flach ist, mit den durch size gegebenen Dimensionen. Der Parameter size muss, wenn er angegeben wird, eine Sequenz von Größen oder eine einzelne Zahl sein, in welchem Fall die Größe des Filters entlang jeder Achse gleich angenommen wird. Der Parameter footprint muss, wenn er angegeben wird, ein Array sein, das die Form des Kernels durch seine Nicht-Null-Elemente definiert.
Ähnlich wie bei binärer Erosion und Dilatation gibt es Operationen für Graustufen-Erosion und -Dilatation.
Die Funktion
grey_erosionberechnet eine mehrdimensionale Graustufen-Erosion.Die Funktion
grey_dilationberechnet eine mehrdimensionale Graustufen-Dilatation.
Graustufen-Öffnungs- und Schließungsoperationen können ähnlich wie ihre binären Gegenstücke definiert werden.
Die Funktion
grey_openingimplementiert Graustufen-Öffnung von Arrays beliebigen Rangs. Graustufen-Öffnung ist gleichbedeutend mit einer Graustufen-Erosion, gefolgt von einer Graustufen-Dilatation.Die Funktion
grey_closingimplementiert Graustufen-Schließung von Arrays beliebigen Rangs. Graustufen-Öffnung ist gleichbedeutend mit einer Graustufen-Dilatation, gefolgt von einer Graustufen-Erosion.Die Funktion
morphological_gradientimplementiert einen Graustufen-Morphologiegradienten von Arrays beliebigen Rangs. Der Graustufen-Morphologiegradient ist gleich der Differenz einer Graustufen-Dilatation und einer Graustufen-Erosion.Die Funktion
morphological_laplaceimplementiert einen Graustufen-Morphologie-Laplace von Arrays beliebigen Rangs. Der Graustufen-Morphologie-Laplace ist gleich der Summe einer Graustufen-Dilatation und einer Graustufen-Erosion minus dem Doppelten der Eingabe.Die Funktion
white_tophatimplementiert einen White-Top-Hat-Filter für Arrays beliebigen Rangs. Der White Top-Hat ist gleich der Differenz der Eingabe und einer Graustufen-Öffnung.Die Funktion
black_tophatimplementiert einen Black-Top-Hat-Filter für Arrays beliebigen Rangs. Der Black Top-Hat ist gleich der Differenz einer Graustufen-Schließung und der Eingabe.
Abstandstransformationen#
Abstandstransformationen werden verwendet, um den minimalen Abstand jedes Elements eines Objekts zum Hintergrund zu berechnen. Die folgenden Funktionen implementieren Abstandstransformationen für drei verschiedene Distanzmetriken: Euklidisch, City-Block und Schachbrett-Distanzen.
Die Funktion
distance_transform_cdtverwendet einen Chamfer-Typ-Algorithmus, um die Abstandstransformation der Eingabe zu berechnen, indem jedes Objektelement (definiert durch Werte größer als Null) durch den kürzesten Abstand zum Hintergrund (alle Nicht-Objektelemente) ersetzt wird. Die Struktur bestimmt die Art des Chamferings, das durchgeführt wird. Wenn die Struktur gleich 'cityblock' ist, wird eine Struktur mithilfe vongenerate_binary_structuremit einem quadrierten Abstand von 1 generiert. Wenn die Struktur gleich 'chessboard' ist, wird eine Struktur mithilfe vongenerate_binary_structuremit einem quadrierten Abstand gleich dem Rang des Arrays generiert. Diese Wahl entspricht den üblichen Interpretationen der City-Block- und der Schachbrett-Distanzmetriken in zwei Dimensionen.Zusätzlich zur Abstandstransformation kann die Merkmalstransformation berechnet werden. In diesem Fall wird der Index des nächstgelegenen Hintergrundelements entlang der ersten Achse des Ergebnisses zurückgegeben. Die Flags return_distances und return_indices können verwendet werden, um anzugeben, ob die Abstandstransformation, die Merkmalstransformation oder beides zurückgegeben werden soll.
Die Argumente distances und indices können verwendet werden, um optionale Ausgabearrays bereitzustellen, die die richtige Größe und den richtigen Typ (beide
numpy.int32) haben müssen. Die Grundlagen des Algorithmus, der zur Implementierung dieser Funktion verwendet wird, sind in [2] beschrieben.Die Funktion
distance_transform_edtberechnet die exakte Euklidische Abstandstransformation der Eingabe, indem jedes Objektelement (definiert durch Werte größer als Null) durch den kürzesten Euklidischen Abstand zum Hintergrund (alle Nicht-Objektelemente) ersetzt wird.Zusätzlich zur Abstandstransformation kann die Merkmalstransformation berechnet werden. In diesem Fall wird der Index des nächstgelegenen Hintergrundelements entlang der ersten Achse des Ergebnisses zurückgegeben. Die Flags return_distances und return_indices können verwendet werden, um anzugeben, ob die Abstandstransformation, die Merkmalstransformation oder beides zurückgegeben werden soll.
Optional kann die Abtastung entlang jeder Achse durch den Parameter sampling angegeben werden, der eine Sequenz mit einer Länge gleich dem Rang der Eingabe sein sollte, oder eine einzelne Zahl, in welchem Fall die Abtastung entlang aller Achsen gleich angenommen wird.
Die Argumente distances und indices können verwendet werden, um optionale Ausgabearrays bereitzustellen, die die richtige Größe und den richtigen Typ (
numpy.float64undnumpy.int32) haben müssen. Der Algorithmus, der zur Implementierung dieser Funktion verwendet wird, ist in [3] beschrieben.Die Funktion
distance_transform_bfverwendet einen Brute-Force-Algorithmus, um die Abstandstransformation der Eingabe zu berechnen, indem jedes Objektelement (definiert durch Werte größer als Null) durch den kürzesten Abstand zum Hintergrund (alle Nicht-Objektelemente) ersetzt wird. Die Metrik muss eine der folgenden sein: "euclidean", "cityblock" oder "chessboard".Zusätzlich zur Abstandstransformation kann die Merkmalstransformation berechnet werden. In diesem Fall wird der Index des nächstgelegenen Hintergrundelements entlang der ersten Achse des Ergebnisses zurückgegeben. Die Flags return_distances und return_indices können verwendet werden, um anzugeben, ob die Abstandstransformation, die Merkmalstransformation oder beides zurückgegeben werden soll.
Optional kann die Abtastung entlang jeder Achse durch den Parameter sampling angegeben werden, der eine Sequenz mit einer Länge gleich dem Rang der Eingabe sein sollte, oder eine einzelne Zahl, in welchem Fall die Abtastung entlang aller Achsen gleich angenommen wird. Dieser Parameter wird nur im Fall der Euklidischen Abstandstransformation verwendet.
Die Argumente distances und indices können verwendet werden, um optionale Ausgabearrays bereitzustellen, die die richtige Größe und den richtigen Typ (
numpy.float64undnumpy.int32) haben müssen.Hinweis
Diese Funktion verwendet einen langsamen Brute-Force-Algorithmus. Die Funktion
distance_transform_cdtkann verwendet werden, um City-Block- und Schachbrett-Abstandstransformationen effizienter zu berechnen. Die Funktiondistance_transform_edtkann verwendet werden, um die exakte Euklidische Abstandstransformation effizienter zu berechnen.
Segmentierung und Beschriftung#
Segmentierung ist der Prozess der Trennung von Objekten von Interesse vom Hintergrund. Der einfachste Ansatz ist wahrscheinlich die Intensitätsschwellenwertbildung, die leicht mit numpy-Funktionen durchgeführt werden kann.
>>> a = np.array([[1,2,2,1,1,0],
... [0,2,3,1,2,0],
... [1,1,1,3,3,2],
... [1,1,1,1,2,1]])
>>> np.where(a > 1, 1, 0)
array([[0, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 0],
[0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 1, 0]])
Das Ergebnis ist ein binäres Bild, in dem die einzelnen Objekte noch identifiziert und beschriftet werden müssen. Die Funktion label generiert ein Array, in dem jedem Objekt eine eindeutige Nummer zugewiesen wird.
Die Funktion
labelgeneriert ein Array, in dem die Objekte der Eingabe mit einem ganzzahligen Index beschriftet werden. Sie gibt ein Tupel zurück, das aus dem Array der Objektbeschriftungen und der Anzahl der gefundenen Objekte besteht, es sei denn, der Parameter output ist angegeben, in welchem Fall nur die Anzahl der Objekte zurückgegeben wird. Die Konnektivität der Objekte wird durch ein Strukturierungselement definiert. Zum Beispiel ergibt in 2D die Verwendung eines 4-fach verbundenen Strukturierungselements.>>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]]) >>> s = [[0, 1, 0], [1,1,1], [0,1,0]] >>> from scipy.ndimage import label >>> label(a, s) (array([[0, 1, 1, 0, 0, 0], [0, 1, 1, 0, 2, 0], [0, 0, 0, 2, 2, 2], [0, 0, 0, 0, 2, 0]], dtype=int32), 2)
Diese beiden Objekte sind nicht verbunden, da es keine Möglichkeit gibt, das Strukturierungselement so zu platzieren, dass es beide Objekte überlappt. Ein 8-fach verbundenes Strukturierungselement führt jedoch nur zu einem einzigen Objekt.
>>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]]) >>> s = [[1,1,1], [1,1,1], [1,1,1]] >>> label(a, s)[0] array([[0, 1, 1, 0, 0, 0], [0, 1, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0]], dtype=int32)
Wenn kein Strukturierungselement angegeben wird, wird eines durch Aufrufen von
generate_binary_structure(siehe Binäre Morphologie) mit einer Konnektivität von eins (was in 2D die 4-fach verbundene Struktur des ersten Beispiels ist) generiert. Die Eingabe kann von jedem Typ sein, jeder Wert ungleich Null wird als Teil eines Objekts betrachtet. Dies ist nützlich, wenn Sie ein Array von Objektindizes "neu beschriften" müssen, z. B. nachdem unerwünschte Objekte entfernt wurden. Wenden Sie die Beschriftungsfunktion einfach erneut auf das Index-Array an. Zum Beispiel>>> l, n = label([1, 0, 1, 0, 1]) >>> l array([1, 0, 2, 0, 3], dtype=int32) >>> l = np.where(l != 2, l, 0) >>> l array([1, 0, 0, 0, 3], dtype=int32) >>> label(l)[0] array([1, 0, 0, 0, 2], dtype=int32)
Hinweis
Es wird angenommen, dass das von
labelverwendete Strukturierungselement symmetrisch ist.
Es gibt eine große Anzahl anderer Ansätze zur Segmentierung, zum Beispiel aus einer Schätzung der Grenzen der Objekte, die durch Ableitungsfilter erhalten werden können. Ein solcher Ansatz ist die Watershed-Segmentierung. Die Funktion watershed_ift generiert ein Array, in dem jedem Objekt ein eindeutiges Label zugewiesen wird, aus einem Array, das die Objektgrenzen lokalisiert, die zum Beispiel durch einen Gradientenbetragsfilter generiert wurden. Es verwendet ein Array, das anfängliche Markierungen für die Objekte enthält
Die Funktion
watershed_iftwendet einen Watershed-from-Markers-Algorithmus unter Verwendung der Image Foresting Transform an, wie in [4] beschrieben.Die Eingaben dieser Funktion sind das Array, auf das die Transformation angewendet wird, und ein Array von Markern, die die Objekte durch ein eindeutiges Label kennzeichnen, wobei jeder Wert ungleich Null eine Markierung ist. Zum Beispiel
>>> input = np.array([[0, 0, 0, 0, 0, 0, 0], ... [0, 1, 1, 1, 1, 1, 0], ... [0, 1, 0, 0, 0, 1, 0], ... [0, 1, 0, 0, 0, 1, 0], ... [0, 1, 0, 0, 0, 1, 0], ... [0, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 0]], np.uint8) >>> markers = np.array([[1, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 2, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0]], np.int8) >>> from scipy.ndimage import watershed_ift >>> watershed_ift(input, markers) array([[1, 1, 1, 1, 1, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 2, 2, 2, 2, 2, 1], [1, 2, 2, 2, 2, 2, 1], [1, 2, 2, 2, 2, 2, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1]], dtype=int8)
Hier wurden zwei Markierungen verwendet, um ein Objekt (marker = 2) und den Hintergrund (marker = 1) zu kennzeichnen. Die Reihenfolge, in der diese verarbeitet werden, ist beliebig: Wenn die Markierung für den Hintergrund in die untere rechte Ecke des Arrays verschoben wird, ergibt sich ein anderes Ergebnis
>>> markers = np.array([[0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 2, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 1]], np.int8) >>> watershed_ift(input, markers) array([[1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1]], dtype=int8)
Das Ergebnis ist, dass das Objekt (marker = 2) kleiner ist, da die zweite Markierung früher verarbeitet wurde. Dies ist möglicherweise nicht der gewünschte Effekt, wenn die erste Markierung ein Hintergrundobjekt bezeichnen sollte. Daher behandelt
watershed_iftMarkierungen mit negativem Wert explizit als Hintergrundmarkierungen und verarbeitet sie nach den normalen Markierungen. Wenn zum Beispiel die erste Markierung durch eine negative Markierung ersetzt wird, ergibt sich ein Ergebnis, das dem ersten Beispiel ähnelt>>> markers = np.array([[0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 2, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, -1]], np.int8) >>> watershed_ift(input, markers) array([[-1, -1, -1, -1, -1, -1, -1], [-1, -1, 2, 2, 2, -1, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, -1, 2, 2, 2, -1, -1], [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)
Die Konnektivität der Objekte wird durch ein Strukturierungselement definiert. Wenn kein Strukturierungselement angegeben wird, wird eines durch Aufrufen von
generate_binary_structure(siehe Binäre Morphologie) mit einer Konnektivität von eins (was in 2D eine 4-fach verbundene Struktur ist) generiert. Wenn zum Beispiel eine 8-fach verbundene Struktur mit dem letzten Beispiel verwendet wird, ergibt sich ein anderes Objekt>>> watershed_ift(input, markers, ... structure = [[1,1,1], [1,1,1], [1,1,1]]) array([[-1, -1, -1, -1, -1, -1, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, 2, 2, 2, 2, 2, -1], [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)
Hinweis
Die Implementierung von
watershed_iftbeschränkt die Datentypen der Eingabe aufnumpy.uint8undnumpy.uint16.
Objektmessungen#
Bei einem Array von beschrifteten Objekten können die Eigenschaften der einzelnen Objekte gemessen werden. Die Funktion find_objects kann verwendet werden, um eine Liste von Slices zu generieren, die für jedes Objekt das kleinste Unterarray angeben, das das Objekt vollständig umschließt
Die Funktion
find_objectsfindet alle Objekte in einem beschrifteten Array und gibt eine Liste von Slices zurück, die den kleinsten Regionen im Array entsprechen, die das Objekt enthalten.Zum Beispiel.
>>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]]) >>> l, n = label(a) >>> from scipy.ndimage import find_objects >>> f = find_objects(l) >>> a[f[0]] array([[1, 1], [1, 1]]) >>> a[f[1]] array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
Die Funktion
find_objectsgibt Slices für alle Objekte zurück, es sei denn, der Parameter max_label ist größer als Null, in diesem Fall werden nur die ersten max_label Objekte zurückgegeben. Wenn ein Index im label-Array fehlt, wird stattdessenNoneanstelle eines Slices zurückgegeben. Zum Beispiel>>> from scipy.ndimage import find_objects >>> find_objects([1, 0, 3, 4], max_label = 3) [(slice(0, 1, None),), None, (slice(2, 3, None),)]
Die von find_objects generierte Liste von Slices ist nützlich, um die Position und die Dimensionen der Objekte im Array zu finden, kann aber auch verwendet werden, um Messungen an den einzelnen Objekten durchzuführen. Nehmen wir an, wir möchten die Summe der Intensitäten eines Objekts im Bild finden
>>> image = np.arange(4 * 6).reshape(4, 6)
>>> mask = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> labels = label(mask)[0]
>>> slices = find_objects(labels)
Dann können wir die Summe der Elemente des zweiten Objekts berechnen
>>> np.where(labels[slices[1]] == 2, image[slices[1]], 0).sum()
80
Das ist jedoch nicht besonders effizient und kann auch für andere Arten von Messungen komplizierter sein. Daher sind einige Messfunktionen definiert, die das Array der Objektlabels und den Index des zu messenden Objekts akzeptieren. Zum Beispiel kann die Summe der Intensitäten berechnet werden durch
>>> from scipy.ndimage import sum as ndi_sum
>>> ndi_sum(image, labels, 2)
80
Bei großen Arrays und kleinen Objekten ist es effizienter, die Messfunktionen nach dem Slicing des Arrays aufzurufen
>>> ndi_sum(image[slices[1]], labels[slices[1]], 2)
80
Alternativ können wir die Messungen für eine Anzahl von Labels mit einem einzigen Funktionsaufruf durchführen, der eine Liste von Ergebnissen zurückgibt. Zum Beispiel, um die Summe der Werte des Hintergrunds und des zweiten Objekts in unserem Beispiel zu messen, geben wir eine Liste von Labels an
>>> ndi_sum(image, labels, [0, 2])
array([178.0, 80.0])
Die unten beschriebenen Messfunktionen unterstützen alle den Parameter index, um anzugeben, welche Objekte gemessen werden sollen. Der Standardwert von index ist None. Dies bedeutet, dass alle Elemente mit einem Label größer als Null als einzelnes Objekt behandelt und gemessen werden. In diesem Fall wird das labels-Array als Maske behandelt, die durch die Elemente größer als Null definiert ist. Wenn index eine Zahl oder eine Folge von Zahlen ist, werden die Labels der zu messenden Objekte angegeben. Wenn index eine Folge ist, wird eine Liste der Ergebnisse zurückgegeben. Funktionen, die mehr als ein Ergebnis zurückgeben, geben ihr Ergebnis als Tupel zurück, wenn index eine einzelne Zahl ist, oder als Tupel von Listen, wenn index eine Folge ist.
Die Funktion
sumberechnet die Summe der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
meanberechnet den Mittelwert der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
varianceberechnet die Varianz der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
standard_deviationberechnet die Standardabweichung der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
minimumberechnet das Minimum der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
maximumberechnet das Maximum der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
minimum_positionberechnet die Position des Minimums der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
maximum_positionberechnet die Position des Maximums der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
extremaberechnet das Minimum, das Maximum und ihre Positionen der Elemente des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen. Das Ergebnis ist ein Tupel, das das Minimum, das Maximum, die Position des Minimums und die Position des Maximums angibt. Das Ergebnis ist dasselbe wie ein Tupel, das aus den Ergebnissen der oben beschriebenen Funktionen minimum, maximum, minimum_position und maximum_position gebildet wird.Die Funktion
center_of_massberechnet den Schwerpunkt des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen.Die Funktion
histogramberechnet ein Histogramm des Objekts mit dem/den durch index angegebenen Label(s) unter Verwendung des labels-Arrays für die Objektlabels. Wenn indexNoneist, werden alle Elemente mit einem Label-Wert ungleich Null als einzelnes Objekt behandelt. Wenn labelNoneist, werden alle Elemente von input in die Berechnung einbezogen. Histogramme werden durch ihr Minimum (min), ihr Maximum (max) und die Anzahl der Bins (bins) definiert. Sie werden als 1-D-Arrays vom Typnumpy.int32zurückgegeben.
Erweiterung von scipy.ndimage in C#
Einige Funktionen in scipy.ndimage nehmen ein Callback-Argument entgegen. Dies kann entweder eine Python-Funktion oder ein scipy.LowLevelCallable sein, das einen Zeiger auf eine C-Funktion enthält. Die Verwendung einer C-Funktion ist in der Regel effizienter, da sie den Overhead des Aufrufs einer Python-Funktion für viele Elemente eines Arrays vermeidet. Um eine C-Funktion zu verwenden, müssen Sie eine C-Erweiterung schreiben, die die Callback-Funktion und eine Python-Funktion enthält, die ein scipy.LowLevelCallable mit einem Zeiger auf den Callback zurückgibt.
Ein Beispiel für eine Funktion, die Callbacks unterstützt, ist geometric_transform, die eine Callback-Funktion akzeptiert, die eine Abbildung von allen Ausgabekoordinaten auf entsprechende Koordinaten im Eingabearray definiert. Betrachten Sie das folgende Python-Beispiel, das geometric_transform verwendet, um eine Verschiebungsfunktion zu implementieren.
from scipy import ndimage
def transform(output_coordinates, shift):
input_coordinates = output_coordinates[0] - shift, output_coordinates[1] - shift
return input_coordinates
im = np.arange(12).reshape(4, 3).astype(np.float64)
shift = 0.5
print(ndimage.geometric_transform(im, transform, extra_arguments=(shift,)))
Wir können die Callback-Funktion auch mit dem folgenden C-Code implementieren
/* example.c */
#include <Python.h>
#include <numpy/npy_common.h>
static int
_transform(npy_intp *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data)
{
npy_intp i;
double shift = *(double *)user_data;
for (i = 0; i < input_rank; i++) {
input_coordinates[i] = output_coordinates[i] - shift;
}
return 1;
}
static char *transform_signature = "int (npy_intp *, double *, int, int, void *)";
static PyObject *
py_get_transform(PyObject *obj, PyObject *args)
{
if (!PyArg_ParseTuple(args, "")) return NULL;
return PyCapsule_New(_transform, transform_signature, NULL);
}
static PyMethodDef ExampleMethods[] = {
{"get_transform", (PyCFunction)py_get_transform, METH_VARARGS, ""},
{NULL, NULL, 0, NULL}
};
/* Initialize the module */
static struct PyModuleDef example = {
PyModuleDef_HEAD_INIT,
"example",
NULL,
-1,
ExampleMethods,
NULL,
NULL,
NULL,
NULL
};
PyMODINIT_FUNC
PyInit_example(void)
{
return PyModule_Create(&example);
}
Weitere Informationen zum Schreiben von Python-Erweiterungsmodulen finden Sie hier. Wenn sich der C-Code in der Datei example.c befindet, kann er kompiliert werden, nachdem er zu meson.build hinzugefügt wurde (siehe Beispiele in .build-Dateien) und folgen Sie dem dortigen Vorgehen. Danach erzeugt das Ausführen des Skripts
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable
from example import get_transform
shift = 0.5
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(get_transform(), ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
liefert das gleiche Ergebnis wie das ursprüngliche Python-Skript.
In der C-Version ist _transform die Callback-Funktion und die Parameter output_coordinates und input_coordinates spielen dieselbe Rolle wie in der Python-Version, während output_rank und input_rank die Äquivalente von len(output_coordinates) und len(input_coordinates) liefern. Die Variable shift wird über user_data statt über extra_arguments übergeben. Schließlich gibt die C-Callback-Funktion einen Integer-Status zurück, der bei Erfolg eins und andernfalls null ist.
Die Funktion py_transform wickelt die Callback-Funktion in eine PyCapsule. Die wichtigsten Schritte sind
Initialisieren Sie eine
PyCapsule. Das erste Argument ist ein Zeiger auf die Callback-Funktion.Das zweite Argument ist die Funktionssignatur, die exakt mit der von
ndimageerwarteten übereinstimmen muss.Oben haben wir
scipy.LowLevelCallableverwendet, umuser_dataanzugeben, das wir mitctypesgeneriert haben.Ein anderer Ansatz wäre, die Daten im Kapselkontext bereitzustellen, der mit PyCapsule_SetContext gesetzt werden kann, und
user_datainscipy.LowLevelCallablewegzulassen. In diesem Ansatz müssten wir uns jedoch um die Zuweisung/Freigabe der Daten kümmern — die Freigabe der Daten nach der Zerstörung der Kapsel kann durch Angabe einer nicht-NULL-Callback-Funktion im dritten Argument von PyCapsule_New erfolgen.
C-Callback-Funktionen für ndimage folgen alle diesem Schema. Der nächste Abschnitt listet die ndimage-Funktionen auf, die eine C-Callback-Funktion akzeptieren, und gibt den Prototyp der Funktion an.
Siehe auch
Die Funktionen, die Low-Level-Callback-Argumente unterstützen, sind
Unten zeigen wir alternative Möglichkeiten, den Code zu schreiben, indem wir Numba, Cython, ctypes oder cffi anstelle des Schreibens von Wrapper-Code in C verwenden.
Numba
Numba bietet eine Möglichkeit, Low-Level-Funktionen einfach in Python zu schreiben. Wir können das obige mit Numba wie folgt schreiben
# example.py
import numpy as np
import ctypes
from scipy import ndimage, LowLevelCallable
from numba import cfunc, types, carray
@cfunc(types.intc(types.CPointer(types.intp),
types.CPointer(types.double),
types.intc,
types.intc,
types.voidptr))
def transform(output_coordinates_ptr, input_coordinates_ptr,
output_rank, input_rank, user_data):
input_coordinates = carray(input_coordinates_ptr, (input_rank,))
output_coordinates = carray(output_coordinates_ptr, (output_rank,))
shift = carray(user_data, (1,), types.double)[0]
for i in range(input_rank):
input_coordinates[i] = output_coordinates[i] - shift
return 1
shift = 0.5
# Then call the function
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(transform.ctypes, ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
Cython
Funktionell kann derselbe Code wie oben in Cython mit etwas weniger Boilerplate wie folgt geschrieben werden
# example.pyx
from numpy cimport npy_intp as intp
cdef api int transform(intp *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data):
cdef intp i
cdef double shift = (<double *>user_data)[0]
for i in range(input_rank):
input_coordinates[i] = output_coordinates[i] - shift
return 1
# script.py
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable
import example
shift = 0.5
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable.from_cython(example, "transform", ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
cffi
Mit cffi können Sie mit einer C-Funktion interagieren, die sich in einer gemeinsam genutzten Bibliothek (DLL) befindet. Zuerst müssen wir die gemeinsam genutzte Bibliothek schreiben, was wir in C tun — dieses Beispiel ist für Linux/OSX
/*
example.c
Needs to be compiled with "gcc -std=c99 -shared -fPIC -o example.so example.c"
or similar
*/
#include <stdint.h>
int
_transform(intptr_t *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data)
{
int i;
double shift = *(double *)user_data;
for (i = 0; i < input_rank; i++) {
input_coordinates[i] = output_coordinates[i] - shift;
}
return 1;
}
Der Python-Code, der die Bibliothek aufruft, ist
import os
import numpy as np
from scipy import ndimage, LowLevelCallable
import cffi
# Construct the FFI object, and copypaste the function declaration
ffi = cffi.FFI()
ffi.cdef("""
int _transform(intptr_t *output_coordinates, double *input_coordinates,
int output_rank, int input_rank, void *user_data);
""")
# Open library
lib = ffi.dlopen(os.path.abspath("example.so"))
# Do the function call
user_data = ffi.new('double *', 0.5)
callback = LowLevelCallable(lib._transform, user_data)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
Weitere Informationen finden Sie in der Dokumentation von cffi.
ctypes
Mit ctypes ist der C-Code und die Kompilierung der so/DLL wie bei cffi oben. Der Python-Code ist anders
# script.py
import os
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable
lib = ctypes.CDLL(os.path.abspath('example.so'))
shift = 0.5
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
# Ctypes has no built-in intptr type, so override the signature
# instead of trying to get it via ctypes
callback = LowLevelCallable(lib._transform, ptr,
"int _transform(intptr_t *, double *, int, int, void *)")
# Perform the call
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))
Weitere Informationen finden Sie in der Dokumentation von ctypes.