Spezialfunktionen (scipy.special)

Das Hauptmerkmal des Pakets scipy.special ist die Definition zahlreicher Spezialfunktionen der mathematischen Physik. Verfügbare Funktionen sind Airy, elliptische, Bessel, Gamma, Beta, hypergeometrische, parabolische Zylinder, Mathieu, sphäroidale Wellen, Struve und Kelvin. Es gibt auch einige Low-Level-Statistikfunktionen, die nicht für den allgemeinen Gebrauch bestimmt sind, da das Modul stats eine einfachere Schnittstelle zu diesen Funktionen bietet. Die meisten dieser Funktionen können Array-Argumente entgegennehmen und Array-Ergebnisse zurückgeben, die denselben Broadcasting-Regeln wie andere mathematische Funktionen in Numerical Python folgen. Viele dieser Funktionen akzeptieren auch komplexe Zahlen als Eingabe. Für eine vollständige Liste der verfügbaren Funktionen mit einer einzeiligen Beschreibung geben Sie >>> help(special). ein. Jede Funktion hat auch ihre eigene Dokumentation, die über help aufgerufen werden kann. Wenn Sie eine benötigte Funktion nicht finden, sollten Sie in Erwägung ziehen, sie zu schreiben und zur Bibliothek beizutragen. Sie können die Funktion entweder in C, Fortran oder Python schreiben. Schauen Sie im Quellcode der Bibliothek nach Beispielen für jede dieser Arten von Funktionen.

Bessel-Funktionen reeller Ordnung(jv, jn_zeros)

Bessel-Funktionen sind eine Familie von Lösungen der Bessel'schen Differentialgleichung mit reeller oder komplexer Ordnung alpha

\[x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]

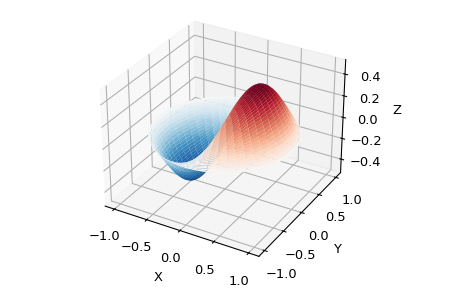
Unter anderem treten diese Funktionen bei Wellenausbreitungsproblemen auf, wie z. B. bei den Schwingungsmoden einer dünnen Trommelhaut. Hier ist ein Beispiel für eine am Rand fixierte kreisförmige Trommelhaut

>>> from scipy import special
>>> import numpy as np
>>> def drumhead_height(n, k, distance, angle, t):
...    kth_zero = special.jn_zeros(n, k)[-1]
...    return np.cos(t) * np.cos(n*angle) * special.jn(n, distance*kth_zero)
>>> theta = np.r_[0:2*np.pi:50j]
>>> radius = np.r_[0:1:50j]
>>> x = np.array([r * np.cos(theta) for r in radius])
>>> y = np.array([r * np.sin(theta) for r in radius])
>>> z = np.array([drumhead_height(1, 1, r, theta, 0.5) for r in radius])

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_axes(rect=(0, 0.05, 0.95, 0.95), projection='3d')
>>> ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='RdBu_r', vmin=-0.5, vmax=0.5)
>>> ax.set_xlabel('X')
>>> ax.set_ylabel('Y')
>>> ax.set_xticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_yticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_zlabel('Z')
>>> plt.show()

Cython-Bindings für Spezialfunktionen (scipy.special.cython_special)

SciPy bietet auch Cython-Bindings für skalare, typisierte Versionen vieler Funktionen in special. Der folgende Cython-Code gibt ein einfaches Beispiel, wie diese Funktionen verwendet werden können

cimport scipy.special.cython_special as csc

cdef:
    double x = 1
    double complex z = 1 + 1j
    double si, ci, rgam
    double complex cgam

rgam = csc.gamma(x)
print(rgam)
cgam = csc.gamma(z)
print(cgam)
csc.sici(x, &si, &ci)
print(si, ci)

(Hilfe zur Kompilierung von Cython finden Sie in der Cython-Dokumentation.) Im Beispiel funktioniert die Funktion csc.gamma im Wesentlichen wie ihr Ufunc-Gegenstück gamma, obwohl sie C-Typen anstelle von NumPy-Arrays als Argumente nimmt. Beachten Sie insbesondere, dass die Funktion für die Unterstützung von reellen und komplexen Argumenten überladen ist; die korrekte Variante wird zur Kompilierzeit ausgewählt. Die Funktion csc.sici funktioniert etwas anders als sici; für das Ufunc konnten wir ai, bi = sici(x) schreiben, während in der Cython-Version mehrere Rückgabewerte über Zeiger übergeben werden. Man könnte dies als analog zur Aufrufung eines Ufuncs mit einem Ausgabe-Array betrachten: sici(x, out=(si, ci)).

Es gibt zwei potenzielle Vorteile bei der Verwendung der Cython-Bindings

• sie vermeiden Python-Funktions-Overhead

• sie erfordern nicht die globale Python-Interpreter-Sperre (GIL)

Die folgenden Abschnitte erörtern, wie diese Vorteile genutzt werden können, um Ihren Code potenziell zu beschleunigen. Natürlich sollte man den Code immer zuerst profilieren, um sicherzustellen, dass sich der zusätzliche Aufwand lohnt.

Vermeidung von Python-Funktions-Overhead

Bei den Ufuncs in special wird der Python-Funktions-Overhead durch Vektorisierung vermieden, d.h. durch Übergabe eines Arrays an die Funktion. Typischerweise funktioniert dieser Ansatz recht gut, aber manchmal ist es bequemer, eine Spezialfunktion mit skalaren Eingaben innerhalb einer Schleife aufzurufen, z.B. bei der Implementierung einer eigenen Ufunc. In diesem Fall kann der Python-Funktions-Overhead erheblich werden. Betrachten Sie das folgende Beispiel

import scipy.special as sc
cimport scipy.special.cython_special as csc

def python_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        sc.jv(n, x)

def cython_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        csc.jv(n, x)

Auf einem Computer dauerte die Ausführung von python_tight_loop etwa 131 Mikrosekunden und die von cython_tight_loop etwa 18,2 Mikrosekunden. Offensichtlich ist dieses Beispiel konstruiert: Man könnte einfach special.jv(np.arange(100), 1) aufrufen und Ergebnisse genauso schnell wie in cython_tight_loop erhalten. Der Punkt ist, dass, wenn der Python-Funktions-Overhead in Ihrem Code signifikant wird, die Cython-Bindings nützlich sein könnten.

Freigabe der GIL

Man muss oft eine Spezialfunktion an vielen Punkten auswerten, und typischerweise sind die Auswertungen trivial parallelisierbar. Da die Cython-Bindings die GIL nicht erfordern, ist es einfach, sie parallel mit Cythons prange-Funktion auszuführen. Angenommen, wir wollten die Fundamentallösung der Helmholtz-Gleichung berechnen

\[\Delta_x G(x, y) + k^2G(x, y) = \delta(x - y),\]

wobei \(k\) die Wellenzahl und \(\delta\) die Diracsche Delta-Funktion ist. In zwei Dimensionen ist die eindeutige (abstrahlende) Lösung bekannt als

\[G(x, y) = \frac{i}{4}H_0^{(1)}(k|x - y|),\]

wobei \(H_0^{(1)}\) die Hankel-Funktion der ersten Art ist, d.h. die Funktion hankel1. Das folgende Beispiel zeigt, wie wir diese Funktion parallel berechnen könnten

from libc.math cimport fabs
cimport cython
from cython.parallel cimport prange

import numpy as np
import scipy.special as sc
cimport scipy.special.cython_special as csc

def serial_G(k, x, y):
    return 0.25j*sc.hankel1(0, k*np.abs(x - y))

@cython.boundscheck(False)
@cython.wraparound(False)
cdef void _parallel_G(double k, double[:,:] x, double[:,:] y,
                      double complex[:,:] out) nogil:
    cdef int i, j

    for i in prange(x.shape[0]):
        for j in range(y.shape[0]):
            out[i,j] = 0.25j*csc.hankel1(0, k*fabs(x[i,j] - y[i,j]))

def parallel_G(k, x, y):
    out = np.empty_like(x, dtype='complex128')
    _parallel_G(k, x, y, out)
    return out

(Hilfe zur Kompilierung parallelen Codes in Cython finden Sie hier.) Wenn der obige Cython-Code in einer Datei test.pyx steht, können wir ein informelles Benchmark schreiben, das die parallele und serielle Version der Funktion vergleicht

import timeit

import numpy as np

from test import serial_G, parallel_G

def main():
    k = 1
    x, y = np.linspace(-100, 100, 1000), np.linspace(-100, 100, 1000)
    x, y = np.meshgrid(x, y)

    def serial():
        serial_G(k, x, y)

    def parallel():
        parallel_G(k, x, y)

    time_serial = timeit.timeit(serial, number=3)
    time_parallel = timeit.timeit(parallel, number=3)
    print("Serial method took {:.3} seconds".format(time_serial))
    print("Parallel method took {:.3} seconds".format(time_parallel))

if __name__ == "__main__":
    main()

Auf einem Quad-Core-Computer dauerte die serielle Methode 1,29 Sekunden und die parallele Methode 0,29 Sekunden.

Funktionen, die nicht in scipy.special enthalten sind

Einige Funktionen sind nicht in special enthalten, da sie sich einfach mit vorhandenen Funktionen in NumPy und SciPy implementieren lassen. Um zu verhindern, dass das Rad neu erfunden wird, bietet dieser Abschnitt Implementierungen mehrerer solcher Funktionen, die hoffentlich veranschaulichen, wie ähnliche Funktionen behandelt werden können. In allen Beispielen ist NumPy als np und special als sc importiert.

Die binäre Entropiefunktion

def binary_entropy(x):
    return -(sc.xlogy(x, x) + sc.xlog1py(1 - x, -x))/np.log(2)

Eine rechteckige Sprungfunktion auf [0, 1]

def step(x):
    return 0.5*(np.sign(x) + np.sign(1 - x))

Durch Translation und Skalierung kann eine beliebige Sprungfunktion erhalten werden.

Die Rampenfunktion

def ramp(x):
    return np.maximum(0, x)