Optimierung (scipy.optimize)

Das Paket scipy.optimize stellt mehrere gängige Optimierungsalgorithmen zur Verfügung. Eine detaillierte Auflistung finden Sie unter: scipy.optimize (kann auch über help(scipy.optimize) gefunden werden).

Lokale Minimierung von multivariaten Skalarfunktionen (minimize)

Die Funktion minimize bietet eine gemeinsame Schnittstelle zu unbeschränkten und beschränkten Minimierungsalgorithmen für multivariate Skalarfunktionen in scipy.optimize. Um die Minimierungsfunktion zu demonstrieren, betrachten wir das Problem der Minimierung der Rosenbrock-Funktion von \(N\) Variablen

\[f\left(\mathbf{x}\right)=\sum_{i=1}^{N-1}100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}.\]

Der minimale Wert dieser Funktion ist 0, der erreicht wird, wenn \(x_{i}=1.\)

Beachten Sie, dass die Rosenbrock-Funktion und ihre Ableitungen in scipy.optimize enthalten sind. Die in den folgenden Abschnitten gezeigten Implementierungen liefern Beispiele dafür, wie eine Zielfunktion sowie ihre Jacobi- und Hesse-Matrizen definiert werden. Zielfunktionen in scipy.optimize erwarten ein numpy-Array als ersten Parameter, der optimiert werden soll, und müssen einen Float-Wert zurückgeben. Die genaue Aufrufsignatur muss f(x, *args) lauten, wobei x ein numpy-Array und args ein Tupel zusätzlicher Argumente darstellt, die an die Zielfunktion übergeben werden.

Unbeschränkte Minimierung

Nelder-Mead Simplex-Algorithmus (method='Nelder-Mead')

Im folgenden Beispiel wird die Routine minimize mit dem *Nelder-Mead*-Simplex-Algorithmus verwendet (ausgewählt über den Parameter method)

>>> import numpy as np
>>> from scipy.optimize import minimize

>>> def rosen(x):
...     """The Rosenbrock function"""
...     return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)

>>> x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
>>> res = minimize(rosen, x0, method='nelder-mead',
...                options={'xatol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 339
         Function evaluations: 571

>>> print(res.x)
[1. 1. 1. 1. 1.]

Der Simplex-Algorithmus ist wahrscheinlich die einfachste Methode, um eine relativ gutmütige Funktion zu minimieren. Er erfordert nur Funktionsauswertungen und ist eine gute Wahl für einfache Minimierungsprobleme. Da er jedoch keine Gradientenauswertungen verwendet, kann es länger dauern, das Minimum zu finden.

Ein weiterer Optimierungsalgorithmus, der nur Funktionsaufrufe benötigt, um das Minimum zu finden, ist Powells Methode, die durch Setzen von method='powell' in minimize verfügbar ist.

Um zu demonstrieren, wie zusätzliche Argumente an eine Zielfunktion übergeben werden, minimieren wir die Rosenbrock-Funktion mit einem zusätzlichen Skalierungsfaktor a und einem Offset b

\[f\left(\mathbf{x}, a, b\right)=\sum_{i=1}^{N-1}a\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2} + b.\]

Mit der Routine minimize kann dies mit dem folgenden Codeblock für die Beispielparameter a=0.5 und b=1 gelöst werden.

>>> def rosen_with_args(x, a, b):
...     """The Rosenbrock function with additional arguments"""
...     return sum(a*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0) + b

>>> x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
>>> res = minimize(rosen_with_args, x0, method='nelder-mead',
...                args=(0.5, 1.), options={'xatol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 1.000000
         Iterations: 319 # may vary
         Function evaluations: 525 # may vary

>>> print(res.x)
[1.         1.         1.         1.         0.99999999]

Als Alternative zur Verwendung des Parameters args von minimize können Sie die Zielfunktion einfach in eine neue Funktion verpacken, die nur x akzeptiert. Dieser Ansatz ist auch nützlich, wenn zusätzliche Parameter als Schlüsselwortargumente an die Zielfunktion übergeben werden müssen.

>>> def rosen_with_args(x, a, *, b):  # b is a keyword-only argument
...     return sum(a*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0) + b
>>> def wrapped_rosen_without_args(x):
...     return rosen_with_args(x, 0.5, b=1.)  # pass in `a` and `b`
>>> x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
>>> res = minimize(wrapped_rosen_without_args, x0, method='nelder-mead',
...                options={'xatol': 1e-8,})
>>> print(res.x)
[1.         1.         1.         1.         0.99999999]

Eine weitere Alternative ist die Verwendung von functools.partial.

>>> from functools import partial
>>> partial_rosen = partial(rosen_with_args, a=0.5, b=1.)
>>> res = minimize(partial_rosen, x0, method='nelder-mead',
...                options={'xatol': 1e-8,})
>>> print(res.x)
[1.         1.         1.         1.         0.99999999]

Broyden-Fletcher-Goldfarb-Shanno-Algorithmus (method='BFGS')

Um schneller zur Lösung zu konvergieren, verwendet diese Routine den Gradienten der Zielfunktion. Wenn der Gradient nicht vom Benutzer angegeben wird, wird er mittels Differenzen erster Ordnung geschätzt. Die Broyden-Fletcher-Goldfarb-Shanno (BFGS)-Methode erfordert typischerweise weniger Funktionsauswertungen als der Simplex-Algorithmus, auch wenn der Gradient geschätzt werden muss.

Zur Demonstration dieses Algorithmus wird wieder die Rosenbrock-Funktion verwendet. Der Gradient der Rosenbrock-Funktion ist der Vektor

\begin{eqnarray*} \frac{\partial f}{\partial x_{j}} & = & \sum_{i=1}^{N}200\left(x_{i}-x_{i-1}^{2}\right)\left(\delta_{i,j}-2x_{i-1}\delta_{i-1,j}\right)-2\left(1-x_{i-1}\right)\delta_{i-1,j}.\\ & = & 200\left(x_{j}-x_{j-1}^{2}\right)-400x_{j}\left(x_{j+1}-x_{j}^{2}\right)-2\left(1-x_{j}\right).\end{eqnarray*}

Dieser Ausdruck gilt für die inneren Ableitungen. Sonderfälle sind

\begin{eqnarray*} \frac{\partial f}{\partial x_{0}} & = & -400x_{0}\left(x_{1}-x_{0}^{2}\right)-2\left(1-x_{0}\right),\\ \frac{\partial f}{\partial x_{N-1}} & = & 200\left(x_{N-1}-x_{N-2}^{2}\right).\end{eqnarray*}

Eine Python-Funktion, die diesen Gradienten berechnet, wird durch den Code-Abschnitt erstellt

>>> def rosen_der(x):
...     xm = x[1:-1]
...     xm_m1 = x[:-2]
...     xm_p1 = x[2:]
...     der = np.zeros_like(x)
...     der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)
...     der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])
...     der[-1] = 200*(x[-1]-x[-2]**2)
...     return der

Diese Gradienteninformationen werden in der Funktion minimize über den Parameter jac angegeben, wie unten gezeigt.

>>> res = minimize(rosen, x0, method='BFGS', jac=rosen_der,
...                options={'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 25                     # may vary
         Function evaluations: 30
         Gradient evaluations: 30
>>> res.x
array([1., 1., 1., 1., 1.])

Vermeidung redundanter Berechnungen

Es ist üblich, dass die Zielfunktion und ihr Gradient Teile der Berechnung gemeinsam nutzen. Betrachten Sie beispielsweise das folgende Problem.

>>> def f(x):
...    return -expensive(x[0])**2
>>>
>>> def df(x):
...     return -2 * expensive(x[0]) * dexpensive(x[0])
>>>
>>> def expensive(x):
...     # this function is computationally expensive!
...     expensive.count += 1  # let's keep track of how many times it runs
...     return np.sin(x)
>>> expensive.count = 0
>>>
>>> def dexpensive(x):
...     return np.cos(x)
>>>
>>> res = minimize(f, 0.5, jac=df)
>>> res.fun
-0.9999999999999174
>>> res.nfev, res.njev
6, 6
>>> expensive.count
12

Hier wird expensive 12 Mal aufgerufen: sechsmal in der Zielfunktion und sechsmal aus dem Gradienten. Eine Möglichkeit, redundante Berechnungen zu reduzieren, besteht darin, eine einzige Funktion zu erstellen, die sowohl die Zielfunktion als auch ihren Gradienten zurückgibt.

>>> def f_and_df(x):
...     expensive_value = expensive(x[0])
...     return (-expensive_value**2,  # objective function
...             -2*expensive_value*dexpensive(x[0]))  # gradient
>>>
>>> expensive.count = 0  # reset the counter
>>> res = minimize(f_and_df, 0.5, jac=True)
>>> res.fun
-0.9999999999999174
>>> expensive.count
6

Wenn wir minimieren, geben wir jac==True an, um anzuzeigen, dass die bereitgestellte Funktion sowohl die Zielfunktion als auch ihren Gradienten zurückgibt. Obwohl praktisch, unterstützen nicht alle scipy.optimize-Funktionen diese Funktion, und darüber hinaus dient sie nur zur gemeinsamen Nutzung von Berechnungen zwischen der Funktion und ihrem Gradienten, während in einigen Problemen Berechnungen mit der Hesse-Matrix (zweite Ableitung der Zielfunktion) und Nebenbedingungen gemeinsam genutzt werden müssen. Ein allgemeinerer Ansatz ist die Memoisation der aufwendigen Teile der Berechnung. In einfachen Situationen kann dies mit dem Wrapper functools.lru_cache erreicht werden.

>>> from functools import lru_cache
>>> expensive.count = 0  # reset the counter
>>> expensive = lru_cache(expensive)
>>> res = minimize(f, 0.5, jac=df)
>>> res.fun
-0.9999999999999174
>>> expensive.count
6

Newton-Conjugate-Gradient-Algorithmus (method='Newton-CG')

Der Newton-Conjugate-Gradient-Algorithmus ist eine modifizierte Newton-Methode und verwendet einen Conjugate-Gradient-Algorithmus, um die lokale Hesse-Matrix zu (ungefähren) invertieren [NW]. Die Newton-Methode basiert auf der lokalen Anpassung der Funktion an eine quadratische Form

\[f\left(\mathbf{x}\right)\approx f\left(\mathbf{x}_{0}\right)+\nabla f\left(\mathbf{x}_{0}\right)\cdot\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2}\left(\mathbf{x}-\mathbf{x}_{0}\right)^{T}\mathbf{H}\left(\mathbf{x}_{0}\right)\left(\mathbf{x}-\mathbf{x}_{0}\right).\]

wobei \(\mathbf{H}\left(\mathbf{x}_{0}\right)\) eine Matrix von zweiten Ableitungen (die Hesse-Matrix) ist. Wenn die Hesse-Matrix positiv definit ist, kann das lokale Minimum dieser Funktion gefunden werden, indem der Gradient der quadratischen Form auf Null gesetzt wird, was zu

\[\mathbf{x}_{\textrm{opt}}=\mathbf{x}_{0}-\mathbf{H}^{-1}\nabla f.\]

führt. Die Inverse der Hesse-Matrix wird mittels des Conjugate-Gradient-Verfahrens ausgewertet. Ein Beispiel für die Anwendung dieser Methode zur Minimierung der Rosenbrock-Funktion ist unten angegeben. Um die Newton-CG-Methode voll auszuschöpfen, muss eine Funktion bereitgestellt werden, die die Hesse-Matrix berechnet. Die Hesse-Matrix selbst muss nicht konstruiert werden, nur ein Vektor, der das Produkt der Hesse-Matrix mit einem beliebigen Vektor ist, muss dem Minimierungsalgorithmus zur Verfügung stehen. Infolgedessen kann der Benutzer entweder eine Funktion zur Berechnung der Hesse-Matrix oder eine Funktion zur Berechnung des Produkts der Hesse-Matrix mit einem beliebigen Vektor bereitstellen.

Beispiel für die vollständige Hesse-Matrix

Die Hesse-Matrix der Rosenbrock-Funktion ist

\begin{eqnarray*} H_{ij}=\frac{\partial^{2}f}{\partial x_{i}\partial x_{j}} & = & 200\left(\delta_{i,j}-2x_{i-1}\delta_{i-1,j}\right)-400x_{i}\left(\delta_{i+1,j}-2x_{i}\delta_{i,j}\right)-400\delta_{i,j}\left(x_{i+1}-x_{i}^{2}\right)+2\delta_{i,j},\\ & = & \left(202+1200x_{i}^{2}-400x_{i+1}\right)\delta_{i,j}-400x_{i}\delta_{i+1,j}-400x_{i-1}\delta_{i-1,j},\end{eqnarray*}

wenn \(i,j\in\left[1,N-2\right]\) mit \(i,j\in\left[0,N-1\right]\) die \(N\times N\)-Matrix definieren. Andere Nicht-Null-Einträge der Matrix sind

\begin{eqnarray*} \frac{\partial^{2}f}{\partial x_{0}^{2}} & = & 1200x_{0}^{2}-400x_{1}+2,\\ \frac{\partial^{2}f}{\partial x_{0}\partial x_{1}}=\frac{\partial^{2}f}{\partial x_{1}\partial x_{0}} & = & -400x_{0},\\ \frac{\partial^{2}f}{\partial x_{N-1}\partial x_{N-2}}=\frac{\partial^{2}f}{\partial x_{N-2}\partial x_{N-1}} & = & -400x_{N-2},\\ \frac{\partial^{2}f}{\partial x_{N-1}^{2}} & = & 200.\end{eqnarray*}

Zum Beispiel ist die Hesse-Matrix für \(N=5\)

\[\begin{split}\mathbf{H}=\begin{bmatrix} 1200x_{0}^{2}+2\mkern-2em\\&1200x_{1}^{2}+202\mkern-2em\\&&1200x_{1}^{2}+202\mkern-2em\\&&&1200x_{3}^{2}+202\mkern-1em\\&&&&200\end{bmatrix}-400\begin{bmatrix} x_1 & x_0 \\ x_0 & x_2 & x_1 \\ & x_1 & x_3 & x_2\\ & & x_2 & x_4 & x_3 \\ & & & x_3 & 0\end{bmatrix}.\end{split}\]

Der Code, der diese Hesse-Matrix berechnet, zusammen mit dem Code zur Minimierung der Funktion unter Verwendung der Newton-CG-Methode ist im folgenden Beispiel dargestellt

>>> def rosen_hess(x):
...     x = np.asarray(x)
...     H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)
...     diagonal = np.zeros_like(x)
...     diagonal[0] = 1200*x[0]**2-400*x[1]+2
...     diagonal[-1] = 200
...     diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]
...     H = H + np.diag(diagonal)
...     return H

>>> res = minimize(rosen, x0, method='Newton-CG',
...                jac=rosen_der, hess=rosen_hess,
...                options={'xtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19                       # may vary
         Function evaluations: 22
         Gradient evaluations: 19
         Hessian evaluations: 19
>>> res.x
array([1.,  1.,  1.,  1.,  1.])

Beispiel für Hesse-Produkt

Bei größeren Minimierungsproblemen kann das Speichern der gesamten Hesse-Matrix erhebliche Zeit und Speicher beanspruchen. Der Newton-CG-Algorithmus benötigt nur das Produkt der Hesse-Matrix mit einem beliebigen Vektor. Daher kann der Benutzer Code zur Berechnung dieses Produkts anstelle der vollständigen Hesse-Matrix bereitstellen, indem er eine hess-Funktion angibt, die den Minimierungsvektor als erstes Argument und den beliebigen Vektor als zweites Argument (zusammen mit zusätzlichen Argumenten, die an die zu minimierende Funktion übergeben werden) erhält. Wenn möglich, ist die Verwendung von Newton-CG mit der Option für das Hesse-Produkt wahrscheinlich der schnellste Weg, die Funktion zu minimieren.

In diesem Fall ist das Produkt der Rosenbrock-Hesse-Matrix mit einem beliebigen Vektor nicht schwierig zu berechnen. Wenn \(\mathbf{p}\) der beliebige Vektor ist, dann hat \(\mathbf{H}\left(\mathbf{x}\right)\mathbf{p}\) die Elemente

\[\begin{split}\mathbf{H}\left(\mathbf{x}\right)\mathbf{p}=\begin{bmatrix} \left(1200x_{0}^{2}-400x_{1}+2\right)p_{0}-400x_{0}p_{1}\\ \vdots\\ -400x_{i-1}p_{i-1}+\left(202+1200x_{i}^{2}-400x_{i+1}\right)p_{i}-400x_{i}p_{i+1}\\ \vdots\\ -400x_{N-2}p_{N-2}+200p_{N-1}\end{bmatrix}.\end{split}\]

Code, der dieses Hesse-Produkt zur Minimierung der Rosenbrock-Funktion unter Verwendung von minimize verwendet, folgt

>>> def rosen_hess_p(x, p):
...     x = np.asarray(x)
...     Hp = np.zeros_like(x)
...     Hp[0] = (1200*x[0]**2 - 400*x[1] + 2)*p[0] - 400*x[0]*p[1]
...     Hp[1:-1] = -400*x[:-2]*p[:-2]+(202+1200*x[1:-1]**2-400*x[2:])*p[1:-1] \
...                -400*x[1:-1]*p[2:]
...     Hp[-1] = -400*x[-2]*p[-2] + 200*p[-1]
...     return Hp

>>> res = minimize(rosen, x0, method='Newton-CG',
...                jac=rosen_der, hessp=rosen_hess_p,
...                options={'xtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20                    # may vary
         Function evaluations: 23
         Gradient evaluations: 20
         Hessian evaluations: 44
>>> res.x
array([1., 1., 1., 1., 1.])

Gemäß [NW] S. 170 kann der Algorithmus Newton-CG ineffizient sein, wenn die Hesse-Matrix schlecht konditioniert ist, da die Suchrichtungen, die von der Methode in diesen Situationen geliefert werden, von schlechter Qualität sind. Die Methode trust-ncg, so die Autoren, geht effektiver mit dieser problematischen Situation um und wird als nächstes beschrieben.

Trust-Region Newton-Conjugate-Gradient-Algorithmus (method='trust-ncg')

Die Methode Newton-CG ist eine Liniensuchmethode: Sie findet eine Suchrichtung, die eine quadratische Annäherung der Funktion minimiert, und verwendet dann einen Liniensuchalgorithmus, um die (nahezu) optimale Schrittgröße in dieser Richtung zu finden. Ein alternativer Ansatz besteht darin, zunächst die Schrittgrößenbegrenzung \(\Delta\) festzulegen und dann den optimalen Schritt \(\mathbf{p}\) innerhalb des gegebenen Vertrauensradius durch Lösen des folgenden quadratischen Teilproblems zu finden

\begin{eqnarray*} \min_{\mathbf{p}} f\left(\mathbf{x}_{k}\right)+\nabla f\left(\mathbf{x}_{k}\right)\cdot\mathbf{p}+\frac{1}{2}\mathbf{p}^{T}\mathbf{H}\left(\mathbf{x}_{k}\right)\mathbf{p};&\\ \text{subject to: } \|\mathbf{p}\|\le \Delta.& \end{eqnarray*}

Die Lösung wird dann aktualisiert \(\mathbf{x}_{k+1} = \mathbf{x}_{k} + \mathbf{p}\) und der Vertrauensradius \(\Delta\) wird entsprechend dem Grad der Übereinstimmung des quadratischen Modells mit der tatsächlichen Funktion angepasst. Diese Familie von Methoden wird als Vertrauensbereichsmethoden bezeichnet. Der Algorithmus trust-ncg ist eine Vertrauensbereichsmethode, die einen Conjugate-Gradient-Algorithmus zur Lösung des Vertrauensbereichsteilproblems verwendet [NW].

Beispiel für die vollständige Hesse-Matrix

>>> res = minimize(rosen, x0, method='trust-ncg',
...                jac=rosen_der, hess=rosen_hess,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20                    # may vary
         Function evaluations: 21
         Gradient evaluations: 20
         Hessian evaluations: 19
>>> res.x
array([1., 1., 1., 1., 1.])

Beispiel für Hesse-Produkt

>>> res = minimize(rosen, x0, method='trust-ncg',
...                jac=rosen_der, hessp=rosen_hess_p,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20                    # may vary
         Function evaluations: 21
         Gradient evaluations: 20
         Hessian evaluations: 0
>>> res.x
array([1., 1., 1., 1., 1.])

Trust-Region Truncated Generalized Lanczos / Conjugate Gradient-Algorithmus (method='trust-krylov')

Ähnlich wie die Methode trust-ncg ist die Methode trust-krylov eine Methode, die für große Probleme geeignet ist, da sie die Hesse-Matrix nur als linearen Operator mittels Matrix-Vektor-Produkten verwendet. Sie löst das quadratische Teilproblem genauer als die Methode trust-ncg.

\begin{eqnarray*} \min_{\mathbf{p}} f\left(\mathbf{x}_{k}\right)+\nabla f\left(\mathbf{x}_{k}\right)\cdot\mathbf{p}+\frac{1}{2}\mathbf{p}^{T}\mathbf{H}\left(\mathbf{x}_{k}\right)\mathbf{p};&\\ \text{subject to: } \|\mathbf{p}\|\le \Delta.& \end{eqnarray*}

Diese Methode umschließt die Implementierung [TRLIB] der Methode [GLTR], die exakt ein auf einen trunkierten Krylov-Unterraum beschränktes Vertrauensbereichsteilproblem löst. Für indefinite Probleme ist es in der Regel besser, diese Methode zu verwenden, da sie die Anzahl der nichtlinearen Iterationen auf Kosten von wenigen weiteren Matrix-Vektor-Produkten pro Teilproblem-Lösung im Vergleich zur Methode trust-ncg reduziert.

Beispiel für die vollständige Hesse-Matrix

>>> res = minimize(rosen, x0, method='trust-krylov',
...                jac=rosen_der, hess=rosen_hess,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19                    # may vary
         Function evaluations: 20
         Gradient evaluations: 20
         Hessian evaluations: 18
>>> res.x
array([1., 1., 1., 1., 1.])

Beispiel für Hesse-Produkt

>>> res = minimize(rosen, x0, method='trust-krylov',
...                jac=rosen_der, hessp=rosen_hess_p,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19                    # may vary
         Function evaluations: 20
         Gradient evaluations: 20
         Hessian evaluations: 0
>>> res.x
array([1., 1., 1., 1., 1.])

[TRLIB]

F. Lenders, C. Kirches, A. Potschka: “trlib: A vector-free implementation of the GLTR method for iterative solution of the trust region problem”, arXiv:1611.04718

[GLTR]

N. Gould, S. Lucidi, M. Roma, P. Toint: “Solving the Trust-Region Subproblem using the Lanczos Method”, SIAM J. Optim., 9(2), 504–525, (1999). DOI:10.1137/S1052623497322735

Trust-Region Nearly Exact-Algorithmus (method='trust-exact')

Alle Methoden Newton-CG, trust-ncg und trust-krylov eignen sich für die Bewältigung großer Probleme (Probleme mit Tausenden von Variablen). Das liegt daran, dass der Conjugate-Gradient-Algorithmus das Vertrauensbereichsteilproblem (oder die Invertierung der Hesse-Matrix) durch Iterationen ohne explizite Faktorisierung der Hesse-Matrix annähernd löst. Da nur das Produkt der Hesse-Matrix mit einem beliebigen Vektor benötigt wird, eignet sich der Algorithmus besonders gut für dünnbesetzte Hesse-Matrizen, was geringe Speicheranforderungen und erhebliche Zeitersparnis für diese dünnbesetzten Probleme ermöglicht.

Für mittelgroße Probleme, bei denen die Speicherung und Faktorisierung der Hesse-Matrix nicht kritisch sind, ist es möglich, eine Lösung mit weniger Iterationen zu erhalten, indem die Vertrauensbereichsteilprobleme nahezu exakt gelöst werden. Um dies zu erreichen, wird ein bestimmtes nichtlineares Gleichungssystem iterativ für jedes quadratische Teilproblem gelöst [CGT]. Diese Lösung erfordert normalerweise 3 oder 4 Cholesky-Faktorisierungen der Hesse-Matrix. Infolgedessen konvergiert die Methode in weniger Iterationen und benötigt weniger Auswertungen der Zielfunktion als die anderen implementierten Vertrauensbereichsmethoden. Die Option für das Hesse-Produkt wird von diesem Algorithmus nicht unterstützt. Ein Beispiel mit der Rosenbrock-Funktion folgt

>>> res = minimize(rosen, x0, method='trust-exact',
...                jac=rosen_der, hess=rosen_hess,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 13                    # may vary
         Function evaluations: 14
         Gradient evaluations: 13
         Hessian evaluations: 14
>>> res.x
array([1., 1., 1., 1., 1.])

[NW] (1,2,3)

J. Nocedal, S.J. Wright “Numerical optimization.” 2nd edition. Springer Science (2006).

[CGT]

Conn, A. R., Gould, N. I., & Toint, P. L. “Trust region methods”. Siam. (2000). pp. 169-200.

Beschränkte Minimierung

Die Funktion minimize bietet mehrere Algorithmen für die beschränkte Minimierung, nämlich 'trust-constr' , 'SLSQP', 'COBYLA' und 'COBYQA'. Sie erfordern, dass die Nebenbedingungen mit leicht unterschiedlichen Strukturen definiert werden. Die Methoden 'trust-constr', 'COBYQA' und 'COBYLA' erfordern, dass die Nebenbedingungen als Sequenz von Objekten LinearConstraint und NonlinearConstraint definiert werden. Die Methode 'SLSQP' hingegen erfordert, dass die Nebenbedingungen als Sequenz von Dictionaries definiert werden, mit den Schlüsseln type, fun und jac.

Als Beispiel betrachten wir die beschränkte Minimierung der Rosenbrock-Funktion

\begin{eqnarray*} \min_{x_0, x_1} & ~~100\left(x_{1}-x_{0}^{2}\right)^{2}+\left(1-x_{0}\right)^{2} &\\ \text{subject to: } & x_0 + 2 x_1 \leq 1 & \\ & x_0^2 + x_1 \leq 1 & \\ & x_0^2 - x_1 \leq 1 & \\ & 2 x_0 + x_1 = 1 & \\ & 0 \leq x_0 \leq 1 & \\ & -0.5 \leq x_1 \leq 2.0. & \end{eqnarray*}

Dieses Optimierungsproblem hat die eindeutige Lösung \([x_0, x_1] = [0.4149,~ 0.1701]\), für die nur die erste und vierte Nebenbedingung aktiv sind.

Trust-Region Constrained-Algorithmus (method='trust-constr')

Die Trust-Region Constrained-Methode befasst sich mit beschränkten Minimierungsproblemen der Form

\begin{eqnarray*} \min_x & f(x) & \\ \text{subject to: } & ~~~ c^l \leq c(x) \leq c^u, &\\ & x^l \leq x \leq x^u. & \end{eqnarray*}

Wenn \(c^l_j = c^u_j\) ist, liest die Methode die \(j\)-te Nebenbedingung als Gleichheitsnebenbedingung und behandelt sie entsprechend. Darüber hinaus können einseitige Nebenbedingungen durch Setzen der oberen oder unteren Schranke auf np.inf mit dem entsprechenden Vorzeichen angegeben werden.

Die Implementierung basiert auf [EQSQP] für Gleichheitsnebenbedingungsprobleme und auf [TRIP] für Probleme mit Ungleichheitsnebenbedingungen. Beide sind Algorithmen vom Typ Trust-Region, die für große Probleme geeignet sind.

Definieren von Grenzbedingungsbeschränkungen

Die Grenzbedingungsbeschränkungen \(0 \leq x_0 \leq 1\) und \(-0.5 \leq x_1 \leq 2.0\) werden mithilfe eines Bounds-Objekts definiert.

>>> from scipy.optimize import Bounds
>>> bounds = Bounds([0, -0.5], [1.0, 2.0])

Definieren von linearen Nebenbedingungen

Die Nebenbedingungen \(x_0 + 2 x_1 \leq 1\) und \(2 x_0 + x_1 = 1\) können im Standardformat für lineare Nebenbedingungen geschrieben werden

\begin{equation*} \begin{bmatrix}-\infty \\1\end{bmatrix} \leq \begin{bmatrix} 1& 2 \\ 2& 1\end{bmatrix} \begin{bmatrix} x_0 \\x_1\end{bmatrix} \leq \begin{bmatrix} 1 \\ 1\end{bmatrix},\end{equation*}

und mit einem LinearConstraint-Objekt definiert werden.

>>> from scipy.optimize import LinearConstraint
>>> linear_constraint = LinearConstraint([[1, 2], [2, 1]], [-np.inf, 1], [1, 1])

Definieren von nichtlinearen Nebenbedingungen Die nichtlineare Nebenbedingung

\begin{equation*} c(x) = \begin{bmatrix} x_0^2 + x_1 \\ x_0^2 - x_1\end{bmatrix} \leq \begin{bmatrix} 1 \\ 1\end{bmatrix}, \end{equation*}

mit der Jacobi-Matrix

\begin{equation*} J(x) = \begin{bmatrix} 2x_0 & 1 \\ 2x_0 & -1\end{bmatrix},\end{equation*}

und der linearen Kombination der Hesse-Matrizen

\begin{equation*} H(x, v) = \sum_{i=0}^1 v_i \nabla^2 c_i(x) = v_0\begin{bmatrix} 2 & 0 \\ 0 & 0\end{bmatrix} + v_1\begin{bmatrix} 2 & 0 \\ 0 & 0\end{bmatrix}, \end{equation*}

wird mit einem NonlinearConstraint-Objekt definiert.

>>> def cons_f(x):
...     return [x[0]**2 + x[1], x[0]**2 - x[1]]
>>> def cons_J(x):
...     return [[2*x[0], 1], [2*x[0], -1]]
>>> def cons_H(x, v):
...     return v[0]*np.array([[2, 0], [0, 0]]) + v[1]*np.array([[2, 0], [0, 0]])
>>> from scipy.optimize import NonlinearConstraint
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess=cons_H)

Alternativ ist es auch möglich, die Hesse-Matrix \(H(x, v)\) als dünnbesetzte Matrix zu definieren,

>>> from scipy.sparse import csc_matrix
>>> def cons_H_sparse(x, v):
...     return v[0]*csc_matrix([[2, 0], [0, 0]]) + v[1]*csc_matrix([[2, 0], [0, 0]])
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1,
...                                            jac=cons_J, hess=cons_H_sparse)

oder als ein LinearOperator-Objekt.

>>> from scipy.sparse.linalg import LinearOperator
>>> def cons_H_linear_operator(x, v):
...     def matvec(p):
...         return np.array([p[0]*2*(v[0]+v[1]), 0])
...     return LinearOperator((2, 2), matvec=matvec)
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1,
...                                           jac=cons_J, hess=cons_H_linear_operator)

Wenn die Auswertung der Hesse-Matrix \(H(x, v)\) schwierig zu implementieren oder rechnerisch nicht durchführbar ist, kann man HessianUpdateStrategy verwenden. Derzeit verfügbare Strategien sind BFGS und SR1.

>>> from scipy.optimize import BFGS
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess=BFGS())

Alternativ kann die Hesse-Matrix mittels endlicher Differenzen angenähert werden.

>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess='2-point')

Die Jacobi-Matrix der Nebenbedingungen kann ebenfalls mittels endlicher Differenzen angenähert werden. In diesem Fall kann die Hesse-Matrix jedoch nicht mit endlichen Differenzen berechnet werden und muss vom Benutzer bereitgestellt oder mittels HessianUpdateStrategy definiert werden.

>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac='2-point', hess=BFGS())

Lösen des Optimierungsproblems Das Optimierungsproblem wird gelöst mit

>>> x0 = np.array([0.5, 0])
>>> res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hess=rosen_hess,
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 8, CG iterations: 7, optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 0.016 s.
>>> print(res.x)
[0.41494531 0.17010937]

Wenn nötig, kann die Hesse-Matrix der Zielfunktion mittels eines LinearOperator-Objekts definiert werden,

>>> def rosen_hess_linop(x):
...     def matvec(p):
...         return rosen_hess_p(x, p)
...     return LinearOperator((2, 2), matvec=matvec)
>>> res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hess=rosen_hess_linop,
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 8, CG iterations: 7, optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 0.018 s.
>>> print(res.x)
[0.41494531 0.17010937]

oder eines Hesse-Vektor-Produkts über den Parameter hessp.

>>> res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hessp=rosen_hess_p,
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 8, CG iterations: 7, optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 0.018 s.
>>> print(res.x)
[0.41494531 0.17010937]

Alternativ können die erste und zweite Ableitung der Zielfunktion angenähert werden. Beispielsweise kann die Hesse-Matrix mit einer quasi-Newton-Näherung nach SR1 und der Gradient mit endlichen Differenzen angenähert werden.

>>> from scipy.optimize import SR1
>>> res = minimize(rosen, x0, method='trust-constr',  jac="2-point", hess=SR1(),
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 24, CG iterations: 7, optimality: 4.48e-09, constraint violation: 0.00e+00, execution time: 0.016 s.
>>> print(res.x)
[0.41494531 0.17010937]

[TRIP]

Byrd, Richard H., Mary E. Hribar, and Jorge Nocedal. 1999. An interior point algorithm for large-scale nonlinear programming. SIAM Journal on Optimization 9.4: 877-900.

[EQSQP]

Lalee, Marucha, Jorge Nocedal, and Todd Plantega. 1998. On the implementation of an algorithm for large-scale equality constrained optimization. SIAM Journal on Optimization 8.3: 682-706.

Sequential Least SQuares Programming (SLSQP)-Algorithmus (method='SLSQP')

Die SLSQP-Methode befasst sich mit beschränkten Minimierungsproblemen der Form

\begin{eqnarray*} \min_x & f(x) \\ \text{subject to: } & c_j(x) = 0 , &j \in \mathcal{E}\\ & c_j(x) \geq 0 , &j \in \mathcal{I}\\ & \text{lb}_i \leq x_i \leq \text{ub}_i , &i = 1,...,N. \end{eqnarray*}

wobei \(\mathcal{E}\) oder \(\mathcal{I}\) Mengen von Indizes sind, die Gleichheits- und Ungleichheitsnebenbedingungen enthalten.

Sowohl lineare als auch nichtlineare Nebenbedingungen werden als Dictionaries mit den Schlüsseln type, fun und jac definiert.

>>> ineq_cons = {'type': 'ineq',
...              'fun' : lambda x: np.array([1 - x[0] - 2*x[1],
...                                          1 - x[0]**2 - x[1],
...                                          1 - x[0]**2 + x[1]]),
...              'jac' : lambda x: np.array([[-1.0, -2.0],
...                                          [-2*x[0], -1.0],
...                                          [-2*x[0], 1.0]])}
>>> eq_cons = {'type': 'eq',
...            'fun' : lambda x: np.array([2*x[0] + x[1] - 1]),
...            'jac' : lambda x: np.array([2.0, 1.0])}

Und das Optimierungsproblem wird gelöst mit

>>> x0 = np.array([0.5, 0])
>>> res = minimize(rosen, x0, method='SLSQP', jac=rosen_der,
...                constraints=[eq_cons, ineq_cons], options={'ftol': 1e-9, 'disp': True},
...                bounds=bounds)
# may vary
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 0.342717574857755
            Iterations: 5
            Function evaluations: 6
            Gradient evaluations: 5
>>> print(res.x)
[0.41494475 0.1701105 ]

Die meisten Optionen, die für die Methode 'trust-constr' verfügbar sind, sind für 'SLSQP' nicht verfügbar.

Vergleich von lokalen Minimierern

Finden Sie einen Solver, der Ihren Anforderungen entspricht, anhand der folgenden Tabelle. Wenn es mehrere Kandidaten gibt, probieren Sie mehrere aus und sehen Sie, welche Ihre Bedürfnisse am besten erfüllen (z. B. Ausführungszeit, Zielfunktionswert).

Solver	Grenzenbeschränkungen	Nichtlineare Beschränkungen	Verwendet Gradient	Verwendet Hesse-Matrix	Nutzt Sparsity
CG			✓
BFGS			✓
dogleg			✓	✓
trust-ncg			✓	✓
trust-krylov			✓	✓
trust-exact			✓	✓
Newton-CG			✓	✓	✓
Nelder-Mead	✓
Powell	✓
L-BFGS-B	✓		✓
TNC	✓		✓
COBYLA	✓	✓
COBYQA	✓	✓
SLSQP	✓	✓	✓
trust-constr	✓	✓	✓	✓	✓

Globale Optimierung

Die globale Optimierung zielt darauf ab, das globale Minimum einer Funktion innerhalb gegebener Grenzen zu finden, wobei potenziell viele lokale Minima vorhanden sind. Typischerweise durchsuchen globale Minimierer den Parameterraum effizient, während sie im Hintergrund einen lokalen Minimierer (z.B. minimize) verwenden. SciPy enthält eine Reihe guter globaler Optimierer. Hier werden wir diese auf dieselbe Zielfunktion anwenden, nämlich die (passend benannte) eggholder Funktion

>>> def eggholder(x):
...     return (-(x[1] + 47) * np.sin(np.sqrt(abs(x[0]/2 + (x[1]  + 47))))
...             -x[0] * np.sin(np.sqrt(abs(x[0] - (x[1]  + 47)))))

>>> bounds = [(-512, 512), (-512, 512)]

Diese Funktion sieht aus wie ein Eierkarton

>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D

>>> x = np.arange(-512, 513)
>>> y = np.arange(-512, 513)
>>> xgrid, ygrid = np.meshgrid(x, y)
>>> xy = np.stack([xgrid, ygrid])

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> ax.view_init(45, -45)
>>> ax.plot_surface(xgrid, ygrid, eggholder(xy), cmap='terrain')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('y')
>>> ax.set_zlabel('eggholder(x, y)')
>>> plt.show()

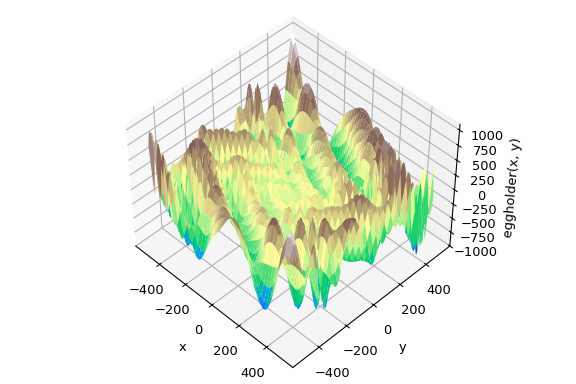
Wir verwenden nun die globalen Optimierer, um das Minimum und den Funktionswert am Minimum zu ermitteln. Wir speichern die Ergebnisse in einem Dictionary, damit wir die verschiedenen Optimierungsergebnisse später vergleichen können.

>>> from scipy import optimize
>>> results = dict()
>>> results['shgo'] = optimize.shgo(eggholder, bounds)
>>> results['shgo']
     fun: -935.3379515604197  # may vary
    funl: array([-935.33795156])
 message: 'Optimization terminated successfully.'
    nfev: 42
     nit: 2
   nlfev: 37
   nlhev: 0
   nljev: 9
 success: True
       x: array([439.48096952, 453.97740589])
      xl: array([[439.48096952, 453.97740589]])

>>> results['DA'] = optimize.dual_annealing(eggholder, bounds)
>>> results['DA']
     fun: -956.9182316237413  # may vary
 message: ['Maximum number of iteration reached']
    nfev: 4091
    nhev: 0
     nit: 1000
    njev: 0
       x: array([482.35324114, 432.87892901])

Alle Optimierer geben ein OptimizeResult zurück, das neben der Lösung Informationen über die Anzahl der Funktionsauswertungen, ob die Optimierung erfolgreich war und mehr enthält. Der Kürze halber werden wir die vollständige Ausgabe der anderen Optimierer nicht zeigen

>>> results['DE'] = optimize.differential_evolution(eggholder, bounds)

shgo hat eine zweite Methode, die alle lokalen Minima zurückgibt, anstatt nur das, was es für das globale Minimum hält

>>> results['shgo_sobol'] = optimize.shgo(eggholder, bounds, n=200, iters=5,
...                                       sampling_method='sobol')

Wir werden nun alle gefundenen Minima auf einer Heatmap der Funktion plotten

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> im = ax.imshow(eggholder(xy), interpolation='bilinear', origin='lower',
...                cmap='gray')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('y')
>>>
>>> def plot_point(res, marker='o', color=None):
...     ax.plot(512+res.x[0], 512+res.x[1], marker=marker, color=color, ms=10)

>>> plot_point(results['DE'], color='c')  # differential_evolution - cyan
>>> plot_point(results['DA'], color='w')  # dual_annealing.        - white

>>> # SHGO produces multiple minima, plot them all (with a smaller marker size)
>>> plot_point(results['shgo'], color='r', marker='+')
>>> plot_point(results['shgo_sobol'], color='r', marker='x')
>>> for i in range(results['shgo_sobol'].xl.shape[0]):
...     ax.plot(512 + results['shgo_sobol'].xl[i, 0],
...             512 + results['shgo_sobol'].xl[i, 1],
...             'ro', ms=2)

>>> ax.set_xlim([-4, 514*2])
>>> ax.set_ylim([-4, 514*2])
>>> plt.show()

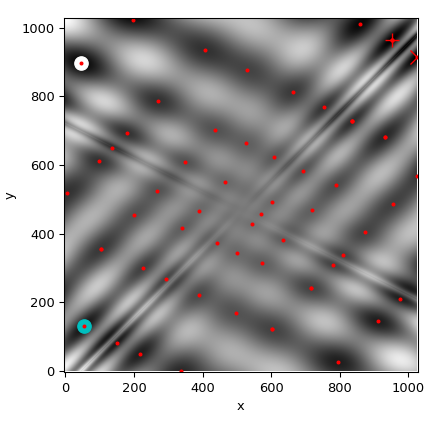
Vergleich globaler Optimierer

Finden Sie einen Solver, der Ihren Anforderungen entspricht, anhand der folgenden Tabelle. Wenn es mehrere Kandidaten gibt, probieren Sie mehrere aus und sehen Sie, welche Ihre Bedürfnisse am besten erfüllen (z. B. Ausführungszeit, Zielfunktionswert).

Solver	Grenzenbeschränkungen	Nichtlineare Beschränkungen	Verwendet Gradient	Verwendet Hesse-Matrix
basinhopping			(✓)	(✓)
direct	✓
dual_annealing	✓		(✓)	(✓)
differential_evolution	✓	✓
shgo	✓	✓	(✓)	(✓)

(✓) = Abhängig vom gewählten lokalen Minimierer

Kleinste-Quadrate-Minimierung (least_squares)

SciPy kann robustifizierte, nichtlineare kleinste-Quadrate-Probleme mit Bereichsbeschränkungen lösen

\begin{align} &\min_\mathbf{x} \frac{1}{2} \sum_{i = 1}^m \rho\left(f_i(\mathbf{x})^2\right) \\ &\text{unter den Bedingungen }\mathbf{lb} \leq \mathbf{x} \leq \mathbf{ub} \end{align}

Hier sind \(f_i(\mathbf{x})\) glatte Funktionen von \(\mathbb{R}^n\) nach \(\mathbb{R}\), wir bezeichnen sie als Residuen. Der Zweck einer skalarwertigen Funktion \(\rho(\cdot)\) ist es, den Einfluss von Ausreißer-Residuen zu reduzieren und zur Robustheit der Lösung beizutragen, wir bezeichnen sie als Verlustfunktion. Eine lineare Verlustfunktion ergibt ein Standard-Problem der kleinsten Quadrate. Zusätzlich sind Beschränkungen in Form von unteren und oberen Grenzen für einige \(x_j\) zulässig.

Alle Methoden, die spezifisch für die Kleinste-Quadrate-Minimierung sind, nutzen eine \(m \times n\) Matrix von partiellen Ableitungen, die Jacobi-Matrix genannt wird und definiert ist als \(J_{ij} = \partial f_i / \partial x_j\). Es wird dringend empfohlen, diese Matrix analytisch zu berechnen und sie an least_squares zu übergeben, andernfalls wird sie durch finite Differenzen geschätzt, was viel zusätzliche Zeit in Anspruch nimmt und in schwierigen Fällen sehr ungenau sein kann.

Die Funktion least_squares kann zur Anpassung einer Funktion \(\varphi(t; \mathbf{x})\) an empirische Daten \(\{(t_i, y_i), i = 0, \ldots, m-1\}\) verwendet werden. Um dies zu tun, sollte man die Residuen einfach als \(f_i(\mathbf{x}) = w_i (\varphi(t_i; \mathbf{x}) - y_i)\) vorausberechnen, wobei \(w_i\) den jeweiligen Beobachtungen zugewiesene Gewichte sind.

Beispiel für die Lösung eines Anpassungsproblems

Hier betrachten wir eine enzymatische Reaktion [1]. Es gibt 11 Residuen, die wie folgt definiert sind:

\[f_i(x) = \frac{x_0 (u_i^2 + u_i x_1)}{u_i^2 + u_i x_2 + x_3} - y_i, \quad i = 0, \ldots, 10,\]

wobei \(y_i\) Messwerte und \(u_i\) Werte der unabhängigen Variable sind. Der unbekannte Parametervektor ist \(\mathbf{x} = (x_0, x_1, x_2, x_3)^T\). Wie bereits erwähnt, wird empfohlen, die Jacobi-Matrix in geschlossener Form zu berechnen

\begin{align} &J_{i0} = \frac{\partial f_i}{\partial x_0} = \frac{u_i^2 + u_i x_1}{u_i^2 + u_i x_2 + x_3} \\ &J_{i1} = \frac{\partial f_i}{\partial x_1} = \frac{u_i x_0}{u_i^2 + u_i x_2 + x_3} \\ &J_{i2} = \frac{\partial f_i}{\partial x_2} = -\frac{x_0 (u_i^2 + u_i x_1) u_i}{(u_i^2 + u_i x_2 + x_3)^2} \\ &J_{i3} = \frac{\partial f_i}{\partial x_3} = -\frac{x_0 (u_i^2 + u_i x_1)}{(u_i^2 + u_i x_2 + x_3)^2} \end{align}

Wir werden den in [2] definierten "harten" Startpunkt verwenden. Um eine physikalisch sinnvolle Lösung zu finden, potenzielle Divisionen durch Null zu vermeiden und die Konvergenz zum globalen Minimum zu gewährleisten, legen wir die Beschränkungen \(0 \leq x_j \leq 100, j = 0, 1, 2, 3\) fest.

Der folgende Code implementiert die Kleinste-Quadrate-Schätzung von \(\mathbf{x}\) und plottet schließlich die Originaldaten und die angepasste Modellfunktion

>>> from scipy.optimize import least_squares

>>> def model(x, u):
...     return x[0] * (u ** 2 + x[1] * u) / (u ** 2 + x[2] * u + x[3])

>>> def fun(x, u, y):
...     return model(x, u) - y

>>> def jac(x, u, y):
...     J = np.empty((u.size, x.size))
...     den = u ** 2 + x[2] * u + x[3]
...     num = u ** 2 + x[1] * u
...     J[:, 0] = num / den
...     J[:, 1] = x[0] * u / den
...     J[:, 2] = -x[0] * num * u / den ** 2
...     J[:, 3] = -x[0] * num / den ** 2
...     return J

>>> u = np.array([4.0, 2.0, 1.0, 5.0e-1, 2.5e-1, 1.67e-1, 1.25e-1, 1.0e-1,
...               8.33e-2, 7.14e-2, 6.25e-2])
>>> y = np.array([1.957e-1, 1.947e-1, 1.735e-1, 1.6e-1, 8.44e-2, 6.27e-2,
...               4.56e-2, 3.42e-2, 3.23e-2, 2.35e-2, 2.46e-2])
>>> x0 = np.array([2.5, 3.9, 4.15, 3.9])
>>> res = least_squares(fun, x0, jac=jac, bounds=(0, 100), args=(u, y), verbose=1)
# may vary
`ftol` termination condition is satisfied.
Function evaluations 130, initial cost 4.4383e+00, final cost 1.5375e-04, first-order optimality 4.92e-08.
>>> res.x
array([ 0.19280596,  0.19130423,  0.12306063,  0.13607247])

>>> import matplotlib.pyplot as plt
>>> u_test = np.linspace(0, 5)
>>> y_test = model(res.x, u_test)
>>> plt.plot(u, y, 'o', markersize=4, label='data')
>>> plt.plot(u_test, y_test, label='fitted model')
>>> plt.xlabel("u")
>>> plt.ylabel("y")
>>> plt.legend(loc='lower right')
>>> plt.show()

[1]

J. Kowalik und J. F. Morrison, „Analysis of kinetic data for allosteric enzyme reactions as a nonlinear regression problem“, Math. Biosci., vol. 2, pp. 57-66, 1968.

[2]

2. 13. Averick et al., „The MINPACK-2 Test Problem Collection“.

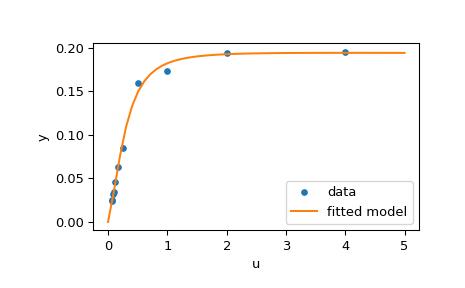
Weitere Beispiele

Drei interaktive Beispiele unten veranschaulichen die Verwendung von least_squares im Detail.

1. Large-scale bundle adjustment in scipy demonstriert die Fähigkeiten von least_squares für große Probleme und wie man die Differentienschätzung einer sparsen Jacobi-Matrix effizient berechnet.

2. Robust nonlinear regression in scipy zeigt, wie man Ausreißer mit einer robusten Verlustfunktion in der nichtlinearen Regression behandelt.

3. Solving a discrete boundary-value problem in scipy untersucht, wie man ein großes Gleichungssystem löst und Beschränkungen verwendet, um gewünschte Eigenschaften der Lösung zu erzielen.

Details zu den mathematischen Algorithmen hinter der Implementierung finden Sie in der Dokumentation von least_squares.

Minimierer für univariaten Funktionen (minimize_scalar)

Oft wird nur das Minimum einer univariaten Funktion (d.h. einer Funktion, die einen Skalar als Eingabe nimmt) benötigt. Unter diesen Umständen wurden andere Optimierungstechniken entwickelt, die schneller arbeiten können. Diese sind über die Funktion minimize_scalar zugänglich, die mehrere Algorithmen vorschlägt.

Unbeschränkte Minimierung (method='brent')

Es gibt tatsächlich zwei Methoden, mit denen eine univariate Funktion minimiert werden kann: brent und golden, aber golden ist nur zu akademischen Zwecken enthalten und sollte selten verwendet werden. Diese können durch den Parameter method in minimize_scalar ausgewählt werden. Die Methode brent verwendet Brents Algorithmus zur Lokalisierung eines Minimums. Optimalerweise sollte eine Klammer (der Parameter bracket) gegeben werden, die das gewünschte Minimum enthält. Eine Klammer ist ein Tripel \(\left( a, b, c \right)\) so dass \(f \left( a \right) > f \left( b \right) < f \left( c \right)\) und \(a < b < c\). Wenn dies nicht gegeben ist, können alternativ zwei Startpunkte gewählt werden und eine Klammer wird aus diesen Punkten mit einem einfachen Marsch-Algorithmus gefunden. Wenn diese beiden Startpunkte nicht angegeben werden, werden 0 und 1 verwendet (dies ist möglicherweise nicht die richtige Wahl für Ihre Funktion und führt zur Rückgabe eines unerwarteten Minimums).

Hier ist ein Beispiel

>>> from scipy.optimize import minimize_scalar
>>> f = lambda x: (x - 2) * (x + 1)**2
>>> res = minimize_scalar(f, method='brent')
>>> print(res.x)
1.0

Beschränkte Minimierung (method='bounded')

Sehr oft gibt es Einschränkungen, die vor der Minimierung auf den Lösungsraum angewendet werden können. Die Methode bounded in minimize_scalar ist ein Beispiel für ein eingeschränktes Minimierungsverfahren, das rudimentäre Intervallbeschränkungen für skalare Funktionen bietet. Die Intervallbeschränkung ermöglicht die Minimierung nur zwischen zwei festen Endpunkten, die mit dem obligatorischen Parameter bounds angegeben werden.

Um beispielsweise das Minimum von \(J_{1}\left( x \right)\) nahe \(x=5\) zu finden, kann minimize_scalar unter Verwendung des Intervalls \(\left[ 4, 7 \right]\) als Beschränkung aufgerufen werden. Das Ergebnis ist \(x_{\textrm{min}}=5.3314\)

>>> from scipy.special import j1
>>> res = minimize_scalar(j1, bounds=(4, 7), method='bounded')
>>> res.x
5.33144184241

Benutzerdefinierte Minimierer

Manchmal kann es nützlich sein, eine benutzerdefinierte Methode als (multivariaten oder univariaten) Minimierer zu verwenden, zum Beispiel bei der Verwendung von Bibliotheks-Wrappern von minimize (z.B. basinhopping).

Dies können wir erreichen, indem wir anstelle eines Methodennamens einen aufrufbaren Wert (entweder eine Funktion oder ein Objekt, das eine __call__ Methode implementiert) als Parameter method übergeben.

Betrachten wir einen (zugegebenermaßen eher virtuellen) Bedarf an einer trivialen benutzerdefinierten multivariaten Minimierungsmethode, die einfach die Nachbarschaft in jeder Dimension unabhängig mit einer festen Schrittgröße durchsucht.

>>> from scipy.optimize import OptimizeResult
>>> def custmin(fun, x0, args=(), maxfev=None, stepsize=0.1,
...         maxiter=100, callback=None, **options):
...     bestx = x0
...     besty = fun(x0)
...     funcalls = 1
...     niter = 0
...     improved = True
...     stop = False
...
...     while improved and not stop and niter < maxiter:
...         improved = False
...         niter += 1
...         for dim in range(np.size(x0)):
...             for s in [bestx[dim] - stepsize, bestx[dim] + stepsize]:
...                 testx = np.copy(bestx)
...                 testx[dim] = s
...                 testy = fun(testx, *args)
...                 funcalls += 1
...                 if testy < besty:
...                     besty = testy
...                     bestx = testx
...                     improved = True
...             if callback is not None:
...                 callback(bestx)
...             if maxfev is not None and funcalls >= maxfev:
...                 stop = True
...                 break
...
...     return OptimizeResult(fun=besty, x=bestx, nit=niter,
...                           nfev=funcalls, success=(niter > 1))
>>> x0 = [1.35, 0.9, 0.8, 1.1, 1.2]
>>> res = minimize(rosen, x0, method=custmin, options=dict(stepsize=0.05))
>>> res.x
array([1., 1., 1., 1., 1.])

Dies funktioniert ebenso gut im Falle einer univariaten Optimierung

>>> def custmin(fun, bracket, args=(), maxfev=None, stepsize=0.1,
...         maxiter=100, callback=None, **options):
...     bestx = (bracket[1] + bracket[0]) / 2.0
...     besty = fun(bestx)
...     funcalls = 1
...     niter = 0
...     improved = True
...     stop = False
...
...     while improved and not stop and niter < maxiter:
...         improved = False
...         niter += 1
...         for testx in [bestx - stepsize, bestx + stepsize]:
...             testy = fun(testx, *args)
...             funcalls += 1
...             if testy < besty:
...                 besty = testy
...                 bestx = testx
...                 improved = True
...         if callback is not None:
...             callback(bestx)
...         if maxfev is not None and funcalls >= maxfev:
...             stop = True
...             break
...
...     return OptimizeResult(fun=besty, x=bestx, nit=niter,
...                           nfev=funcalls, success=(niter > 1))
>>> def f(x):
...    return (x - 2)**2 * (x + 2)**2
>>> res = minimize_scalar(f, bracket=(-3.5, 0), method=custmin,
...                       options=dict(stepsize = 0.05))
>>> res.x
-2.0

Wurzelfindung

Skalare Funktionen

Wenn man eine Gleichung mit einer Variablen hat, gibt es mehrere verschiedene Algorithmen zur Wurzelfindung, die ausprobiert werden können. Die meisten dieser Algorithmen erfordern die Endpunkte eines Intervalls, in dem eine Wurzel erwartet wird (da die Funktion das Vorzeichen wechselt). Im Allgemeinen ist brentq die beste Wahl, aber die anderen Methoden können unter bestimmten Umständen oder zu akademischen Zwecken nützlich sein. Wenn eine Klammer nicht verfügbar ist, aber eine oder mehrere Ableitungen vorhanden sind, dann können newton (oder halley, secant) angewendet werden. Dies ist besonders der Fall, wenn die Funktion auf einer Teilmenge der komplexen Ebene definiert ist und die Klammerungsmethoden nicht verwendet werden können.

Fixpunkt-Lösung

Ein Problem, das eng mit der Suche nach Nullstellen einer Funktion zusammenhängt, ist die Suche nach einem Fixpunkt einer Funktion. Ein Fixpunkt einer Funktion ist der Punkt, an dem die Auswertung der Funktion den Punkt selbst zurückgibt: \(g\left(x\right)=x.\) Klarerweise ist der Fixpunkt von \(g\) die Wurzel von \(f\left(x\right)=g\left(x\right)-x.\) Äquivalent dazu ist die Wurzel von \(f\) der Fixpunkt von \(g\left(x\right)=f\left(x\right)+x.\) Die Routine fixed_point bietet eine einfache iterative Methode mit Aitkens-Sequenzbeschleunigung zur Schätzung des Fixpunkts von \(g\), gegeben einen Startpunkt.

Mengensysteme von Gleichungen

Das Finden einer Wurzel eines Systems nichtlinearer Gleichungen kann mit der Funktion root erreicht werden. Mehrere Methoden sind verfügbar, darunter hybr (der Standard) und lm, die jeweils die Hybridmethode von Powell und die Levenberg-Marquardt-Methode von MINPACK verwenden.

Das folgende Beispiel betrachtet die transzendente Gleichung mit einer Variablen

\[x+2\cos\left(x\right)=0,\]

deren Wurzel wie folgt gefunden werden kann

>>> import numpy as np
>>> from scipy.optimize import root
>>> def func(x):
...     return x + 2 * np.cos(x)
>>> sol = root(func, 0.3)
>>> sol.x
array([-1.02986653])
>>> sol.fun
array([ -6.66133815e-16])

Betrachten wir nun ein System nichtlinearer Gleichungen

\begin{eqnarray*} x_{0}\cos\left(x_{1}\right) & = & 4,\\ x_{0}x_{1}-x_{1} & = & 5. \end{eqnarray*}

Wir definieren die Zielfunktion so, dass sie auch die Jacobi-Matrix zurückgibt, und kennzeichnen dies durch Setzen des Parameters jac auf True. Hier wird auch der Levenberg-Marquardt-Solver verwendet.

>>> def func2(x):
...     f = [x[0] * np.cos(x[1]) - 4,
...          x[1]*x[0] - x[1] - 5]
...     df = np.array([[np.cos(x[1]), -x[0] * np.sin(x[1])],
...                    [x[1], x[0] - 1]])
...     return f, df
>>> sol = root(func2, [1, 1], jac=True, method='lm')
>>> sol.x
array([ 6.50409711,  0.90841421])

Wurzelfindung für große Probleme

Die Methoden hybr und lm in root können nicht mit einer sehr großen Anzahl von Variablen (N) umgehen, da sie bei jedem Newton-Schritt eine dichte N x N Jacobi-Matrix berechnen und invertieren müssen. Dies wird ziemlich ineffizient, wenn N wächst.

Betrachten wir zum Beispiel das folgende Problem: Wir müssen die folgende integrodifferentiale Gleichung im Quadrat \([0,1]\times[0,1]\) lösen

\[(\partial_x^2 + \partial_y^2) P + 5 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2 = 0\]

mit der Randbedingung \(P(x,1) = 1\) am oberen Rand und \(P=0\) anderswo am Rand des Quadrats. Dies kann durch Annäherung der kontinuierlichen Funktion P durch ihre Werte auf einem Gitter erfolgen, \(P_{n,m}\approx{}P(n h, m h)\), mit einem kleinen Gitterabstand h. Die Ableitungen und Integrale können dann angenähert werden; zum Beispiel \(\partial_x^2 P(x,y)\approx{}(P(x+h,y) - 2 P(x,y) + P(x-h,y))/h^2\). Das Problem ist dann äquivalent zum Finden der Wurzel einer Funktion residual(P), wobei P ein Vektor der Länge \(N_x N_y\) ist.

Da nun \(N_x N_y\) groß sein kann, werden die Methoden hybr oder lm in root lange dauern, um dieses Problem zu lösen. Die Lösung kann jedoch mit einem der großen Solver, z.B. krylov, broyden2 oder anderson, gefunden werden. Diese verwenden die sogenannte inexakte Newton-Methode, die anstatt die Jacobi-Matrix exakt zu berechnen, eine Annäherung daran bildet.

Das Problem, das wir haben, kann nun wie folgt gelöst werden

import numpy as np
from scipy.optimize import root
from numpy import cosh, zeros_like, mgrid, zeros

# parameters
nx, ny = 75, 75
hx, hy = 1./(nx-1), 1./(ny-1)

P_left, P_right = 0, 0
P_top, P_bottom = 1, 0

def residual(P):
   d2x = zeros_like(P)
   d2y = zeros_like(P)

   d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2]) / hx/hx
   d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
   d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx

   d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
   d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
   d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy

   return d2x + d2y + 5*cosh(P).mean()**2

# solve
guess = zeros((nx, ny), float)
sol = root(residual, guess, method='krylov', options={'disp': True})
#sol = root(residual, guess, method='broyden2', options={'disp': True, 'max_rank': 50})
#sol = root(residual, guess, method='anderson', options={'disp': True, 'M': 10})
print('Residual: %g' % abs(residual(sol.x)).max())

# visualize
import matplotlib.pyplot as plt
x, y = mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
plt.pcolormesh(x, y, sol.x, shading='gouraud')
plt.colorbar()
plt.show()

Immer noch zu langsam? Vorbehandlung.

Bei der Suche nach der Nullstelle der Funktionen \(f_i({\bf x}) = 0\), i = 1, 2, …, N, verbringt der Solver krylov die meiste Zeit mit der Invertierung der Jacobi-Matrix,

\[J_{ij} = \frac{\partial f_i}{\partial x_j} .\]

Wenn Sie eine Annäherung an die inverse Matrix \(M\approx{}J^{-1}\) haben, können Sie diese zur Vorbehandlung des linearen Invertierungsproblems verwenden. Die Idee ist, dass man anstelle von \(\boldsymbol{J}\mathbf{s}=\mathbf{y}\) zu lösen, \(\boldsymbol{M}\boldsymbol{J}\mathbf{s}=M\mathbf{y}\) löst: Da die Matrix \(\boldsymbol{M}\boldsymbol{J}\) "näher" an der Identitätsmatrix ist als \(\boldsymbol{J}\), sollte die Gleichung für die Krylov-Methode leichter zu handhaben sein.

Die Matrix M kann mit root mit der Methode krylov als Option options['jac_options']['inner_M'] übergeben werden. Sie kann eine (sparse) Matrix oder eine Instanz von scipy.sparse.linalg.LinearOperator sein.

Für das Problem im vorherigen Abschnitt stellen wir fest, dass die zu lösende Funktion aus zwei Teilen besteht: Der erste ist die Anwendung des Laplace-Operators, \([\partial_x^2 + \partial_y^2] P\), und der zweite ist das Integral. Wir können tatsächlich leicht die Jacobi-Matrix für den Laplace-Operator-Teil berechnen: Wir wissen, dass in 1-D

\[\begin{split}\partial_x^2 \approx \frac{1}{h_x^2} \begin{pmatrix} -2 & 1 & 0 & 0 \cdots \\ 1 & -2 & 1 & 0 \cdots \\ 0 & 1 & -2 & 1 \cdots \\ \ldots \end{pmatrix} = h_x^{-2} L\end{split}\]

so dass der gesamte 2-D-Operator dargestellt wird durch

\[J_1 = \partial_x^2 + \partial_y^2 \simeq h_x^{-2} L \otimes I + h_y^{-2} I \otimes L\]

Die Matrix \(J_2\) der Jacobi-Matrix für das Integral ist schwieriger zu berechnen, und da alle ihre Einträge ungleich Null sind, wird sie schwer zu invertieren sein. \(J_1\) hingegen ist eine relativ einfache Matrix und kann durch scipy.sparse.linalg.splu invertiert werden (oder die Inverse kann durch scipy.sparse.linalg.spilu angenähert werden). Wir begnügen uns also damit, \(\boldsymbol{M}\approx{}J_1^{-1}\) zu setzen und auf das Beste zu hoffen.

Im folgenden Beispiel verwenden wir den Vorbehandlungsoperator \(\boldsymbol{M}=J_1^{-1}\).

from scipy.optimize import root
from scipy.sparse import dia_array, kron
from scipy.sparse.linalg import spilu, LinearOperator
from numpy import cosh, zeros_like, mgrid, zeros, eye

# parameters
nx, ny = 75, 75
hx, hy = 1./(nx-1), 1./(ny-1)

P_left, P_right = 0, 0
P_top, P_bottom = 1, 0

def get_preconditioner():
    """Compute the preconditioner M"""
    diags_x = zeros((3, nx))
    diags_x[0,:] = 1/hx/hx
    diags_x[1,:] = -2/hx/hx
    diags_x[2,:] = 1/hx/hx
    Lx = dia_array((diags_x, [-1,0,1]), shape=(nx, nx))

    diags_y = zeros((3, ny))
    diags_y[0,:] = 1/hy/hy
    diags_y[1,:] = -2/hy/hy
    diags_y[2,:] = 1/hy/hy
    Ly = dia_array((diags_y, [-1,0,1]), shape=(ny, ny))

    J1 = kron(Lx, eye(ny)) + kron(eye(nx), Ly)

    # Now we have the matrix `J_1`. We need to find its inverse `M` --
    # however, since an approximate inverse is enough, we can use
    # the *incomplete LU* decomposition

    J1_ilu = spilu(J1)

    # This returns an object with a method .solve() that evaluates
    # the corresponding matrix-vector product. We need to wrap it into
    # a LinearOperator before it can be passed to the Krylov methods:

    M = LinearOperator(shape=(nx*ny, nx*ny), matvec=J1_ilu.solve)
    return M

def solve(preconditioning=True):
    """Compute the solution"""
    count = [0]

    def residual(P):
        count[0] += 1

        d2x = zeros_like(P)
        d2y = zeros_like(P)

        d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2])/hx/hx
        d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
        d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx

        d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
        d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
        d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy

        return d2x + d2y + 5*cosh(P).mean()**2

    # preconditioner
    if preconditioning:
        M = get_preconditioner()
    else:
        M = None

    # solve
    guess = zeros((nx, ny), float)

    sol = root(residual, guess, method='krylov',
               options={'disp': True,
                        'jac_options': {'inner_M': M}})
    print('Residual', abs(residual(sol.x)).max())
    print('Evaluations', count[0])

    return sol.x

def main():
    sol = solve(preconditioning=True)

    # visualize
    import matplotlib.pyplot as plt
    x, y = mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
    plt.clf()
    plt.pcolor(x, y, sol)
    plt.clim(0, 1)
    plt.colorbar()
    plt.show()


if __name__ == "__main__":
    main()

Ergebnis des Laufs, zuerst ohne Vorbehandlung

0:  |F(x)| = 803.614; step 1; tol 0.000257947
1:  |F(x)| = 345.912; step 1; tol 0.166755
2:  |F(x)| = 139.159; step 1; tol 0.145657
3:  |F(x)| = 27.3682; step 1; tol 0.0348109
4:  |F(x)| = 1.03303; step 1; tol 0.00128227
5:  |F(x)| = 0.0406634; step 1; tol 0.00139451
6:  |F(x)| = 0.00344341; step 1; tol 0.00645373
7:  |F(x)| = 0.000153671; step 1; tol 0.00179246
8:  |F(x)| = 6.7424e-06; step 1; tol 0.00173256
Residual 3.57078908664e-07
Evaluations 317

und dann mit Vorbehandlung

0:  |F(x)| = 136.993; step 1; tol 7.49599e-06
1:  |F(x)| = 4.80983; step 1; tol 0.00110945
2:  |F(x)| = 0.195942; step 1; tol 0.00149362
3:  |F(x)| = 0.000563597; step 1; tol 7.44604e-06
4:  |F(x)| = 1.00698e-09; step 1; tol 2.87308e-12
Residual 9.29603061195e-11
Evaluations 77

Die Verwendung eines Vorbehandlungsoperators hat die Anzahl der Auswertungen der Funktion residual um den Faktor 4 reduziert. Bei Problemen, bei denen die Berechnung des Residuums teuer ist, kann eine gute Vorbehandlung entscheidend sein – sie kann sogar darüber entscheiden, ob das Problem praktisch lösbar ist oder nicht.

Vorbehandlung ist eine Kunst, Wissenschaft und Industrie. Hier hatten wir Glück, eine einfache Wahl zu treffen, die vernünftig gut funktionierte, aber dieses Thema ist vielschichtiger, als hier gezeigt wird.

Lineare Programmierung (linprog)

Die Funktion linprog kann eine lineare Zielfunktion unter linearen Gleichheits- und Ungleichheitsbeschränkungen minimieren. Diese Art von Problem ist als lineare Programmierung bekannt. Lineare Programmierung löst Probleme der folgenden Form

\[\begin{split}\min_x \ & c^T x \\ \mbox{so dass} \ & A_{ub} x \leq b_{ub},\\ & A_{eq} x = b_{eq},\\ & l \leq x \leq u ,\end{split}\]

wobei \(x\) ein Vektor von Entscheidungsvariablen ist; \(c\), \(b_{ub}\), \(b_{eq}\), \(l\) und \(u\) Vektoren sind; und \(A_{ub}\) und \(A_{eq}\) Matrizen sind.

In diesem Tutorial versuchen wir, ein typisches lineares Programmierproblem mit linprog zu lösen.

Beispiel für lineare Programmierung

Betrachten Sie das folgende einfache lineare Programmierproblem

\[\begin{split}\max_{x_1, x_2, x_3, x_4} \ & 29x_1 + 45x_2 \\ \text{so dass} \ & x_1 -x_2 -3x_3 \leq 5\\ & 2x_1 -3x_2 -7x_3 + 3x_4 \geq 10\\ & 2x_1 + 8x_2 + x_3 = 60\\ & 4x_1 + 4x_2 + x_4 = 60\\ & 0 \leq x_0\\ & 0 \leq x_1 \leq 5\\ & x_2 \leq 0.5\\ & -3 \leq x_3\\\end{split}\]

Wir benötigen einige mathematische Manipulationen, um das Zielproblem in das von linprog akzeptierte Format zu konvertieren.

Zunächst betrachten wir die Zielfunktion. Wir wollen die Zielfunktion maximieren, aber linprog kann nur ein Minimierungsproblem akzeptieren. Dies ist leicht zu beheben, indem das Maximieren von \(29x_1 + 45x_2\) in das Minimieren von \(-29x_1 -45x_2\) umgewandelt wird. Außerdem werden \(x_3, x_4\) in der Zielfunktion nicht angezeigt. Das bedeutet, dass die Gewichte, die mit \(x_3, x_4\) korrespondieren, null sind. Die Zielfunktion kann also umgewandelt werden in

\[\min_{x_1, x_2, x_3, x_4} \ -29x_1 -45x_2 + 0x_3 + 0x_4\]

Wenn wir den Vektor der Entscheidungsvariablen \(\boldsymbol{x} = [x_1, x_2, x_3, x_4]^T\) definieren, sollte der Gewichtsvektor der Zielfunktion \(\boldsymbol{c}\) von linprog in diesem Problem sein

\[c = [-29, -45, 0, 0]^T\]

Als nächstes betrachten wir die beiden Ungleichheitsbeschränkungen. Die erste ist eine "Kleiner-als"-Ungleichung, also ist sie bereits in dem von linprog akzeptierten Format. Die zweite ist eine "Größer-als"-Ungleichung, also müssen wir beide Seiten mit \(-1\) multiplizieren, um sie in eine "Kleiner-als"-Ungleichung umzuwandeln. Explizit Nullkoeffizienten zeigend, haben wir

\[\begin{split}x_1 -x_2 -3x_3 + 0x_4 &\leq 5\\ -2x_1 + 3x_2 + 7x_3 - 3x_4 &\leq -10\\\end{split}\]

Diese Gleichungen können in Matrixform umgewandelt werden

\[\begin{split}A_{ub} x \leq b_{ub}\\\end{split}\]

wo

\begin{equation*} A_{ub} = \begin{bmatrix} 1 & -1 & -3 & 0 \\ -2 & 3 & 7 & -3 \end{bmatrix} \end{equation*}

\begin{equation*} b_{ub} = \begin{bmatrix} 5 \\ -10 \end{bmatrix} \end{equation*}

Als nächstes betrachten wir die beiden Gleichheitsbeschränkungen. Explizit Nullgewichte zeigend, sind dies

\[\begin{split}2x_1 + 8x_2 + 1x_3 + 0x_4 &= 60\\ 4x_1 + 4x_2 + 0x_3 + 1x_4 &= 60\\\end{split}\]

Diese Gleichungen können in Matrixform umgewandelt werden

\[\begin{split}A_{eq} x = b_{eq}\\\end{split}\]

wo

\begin{equation*} A_{eq} = \begin{bmatrix} 2 & 8 & 1 & 0 \\ 4 & 4 & 0 & 1 \end{bmatrix} \end{equation*}

\begin{equation*} b_{eq} = \begin{bmatrix} 60 \\ 60 \end{bmatrix} \end{equation*}

Schließlich betrachten wir die separaten Ungleichheitsbeschränkungen für einzelne Entscheidungsvariablen, die als "Box-Beschränkungen" oder "einfache Grenzen" bekannt sind. Diese Beschränkungen können mit dem Argument bounds von linprog angewendet werden. Wie in der Dokumentation von linprog angegeben, ist der Standardwert von bounds (0, None), was bedeutet, dass die untere Grenze für jede Entscheidungsvariable 0 und die obere Grenze für jede Entscheidungsvariable unendlich ist: Alle Entscheidungsvariablen sind nicht-negativ. Unsere Grenzen sind anders, daher müssen wir die untere und obere Grenze für jede Entscheidungsvariable als Tupel angeben und diese Tupel in einer Liste zusammenfassen.

Schließlich können wir das transformierte Problem mit linprog lösen.

>>> import numpy as np
>>> from scipy.optimize import linprog
>>> c = np.array([-29.0, -45.0, 0.0, 0.0])
>>> A_ub = np.array([[1.0, -1.0, -3.0, 0.0],
...                 [-2.0, 3.0, 7.0, -3.0]])
>>> b_ub = np.array([5.0, -10.0])
>>> A_eq = np.array([[2.0, 8.0, 1.0, 0.0],
...                 [4.0, 4.0, 0.0, 1.0]])
>>> b_eq = np.array([60.0, 60.0])
>>> x0_bounds = (0, None)
>>> x1_bounds = (0, 5.0)
>>> x2_bounds = (-np.inf, 0.5)  # +/- np.inf can be used instead of None
>>> x3_bounds = (-3.0, None)
>>> bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]
>>> result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
>>> print(result.message)
The problem is infeasible. (HiGHS Status 8: model_status is Infeasible; primal_status is None)

Das Ergebnis besagt, dass unser Problem unzulässig ist, was bedeutet, dass es keinen Lösungsvektor gibt, der alle Beschränkungen erfüllt. Das bedeutet nicht unbedingt, dass wir etwas falsch gemacht haben; einige Probleme sind tatsächlich unzulässig. Angenommen jedoch, wir entscheiden, dass unsere Bereichsbeschränkung für \(x_1\) zu eng war und sie auf \(0 \leq x_1 \leq 6\) gelockert werden könnte. Nachdem wir unseren Code x1_bounds = (0, 6) angepasst und erneut ausgeführt haben

>>> x1_bounds = (0, 6)
>>> bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]
>>> result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
>>> print(result.message)
Optimization terminated successfully. (HiGHS Status 7: Optimal)

Das Ergebnis zeigt, dass die Optimierung erfolgreich war. Wir können überprüfen, ob der Zielfunktionswert (result.fun) gleich \(c^Tx\) ist.

>>> x = np.array(result.x)
>>> obj = result.fun
>>> print(c @ x)
-505.97435889013434  # may vary
>>> print(obj)
-505.97435889013434  # may vary

Wir können auch überprüfen, ob alle Beschränkungen innerhalb vernünftiger Toleranzen erfüllt sind

>>> print(b_ub - (A_ub @ x).flatten())  # this is equivalent to result.slack
[ 6.52747190e-10, -2.26730279e-09]  # may vary
>>> print(b_eq - (A_eq @ x).flatten())  # this is equivalent to result.con
[ 9.78840831e-09, 1.04662945e-08]]  # may vary
>>> print([0 <= result.x[0], 0 <= result.x[1] <= 6.0, result.x[2] <= 0.5, -3.0 <= result.x[3]])
[True, True, True, True]

Zuordnungsprobleme

Beispiel für ein lineares Summenzuordnungsproblem

Betrachten Sie das Problem der Auswahl von Schwimmern für eine Schwimmstaffel. Wir haben eine Tabelle, die die Zeiten für jeden Schwimmstil von fünf Schülern zeigt

Schüler	Rückenschwimmen	Brustschwimmen	Schmetterling	Freistil
A	43.5	47.1	48.4	38.2
B	45.5	42.1	49.6	36.8
C	43.4	39.1	42.1	43.2
D	46.5	44.1	44.5	41.2
E	46.3	47.8	50.4	37.2

Wir müssen einen Schüler für jede der vier Schwimmstile auswählen, so dass die Gesamtzeit der Staffel minimiert wird. Dies ist ein typisches lineares Summenzuordnungsproblem. Wir können linear_sum_assignment verwenden, um es zu lösen.

Das lineare Summenzuordnungsproblem ist eines der berühmtesten Probleme der kombinatorischen Optimierung. Gegeben eine "Kostenmatrix" \(\boldsymbol{C}\), besteht das Problem darin, Folgendes auszuwählen:

• genau ein Element aus jeder Zeile

• ohne mehr als ein Element aus jeder Spalte zu wählen

• damit die Summe der ausgewählten Elemente minimiert wird

Mit anderen Worten, wir müssen jede Zeile einer Spalte zuordnen, so dass die Summe der entsprechenden Einträge minimiert wird.

Formal, sei \(\boldsymbol{X}\) eine boolesche Matrix, wobei \(\boldsymbol{X}[i,j] = 1\) genau dann, wenn Zeile \(\boldsymbol{i}\) der Spalte \(\boldsymbol{j}\) zugeordnet wird. Dann hat die optimale Zuordnung die Kosten

\[\min \sum_i \sum_j C_{i,j} X_{i,j}\]

Der erste Schritt ist die Definition der Kostenmatrix. In diesem Beispiel wollen wir jedem Schwimmstil einen Schüler zuordnen. linear_sum_assignment kann jede Zeile einer Kostenmatrix einer Spalte zuordnen. Daher muss die obige Tabelle zur Bildung der Kostenmatrix transponiert werden, so dass die Zeilen den Schwimmstilen und die Spalten den Schülern entsprechen.

>>> import numpy as np
>>> cost = np.array([[43.5, 45.5, 43.4, 46.5, 46.3],
...                  [47.1, 42.1, 39.1, 44.1, 47.8],
...                  [48.4, 49.6, 42.1, 44.5, 50.4],
...                  [38.2, 36.8, 43.2, 41.2, 37.2]])

Wir können das Zuweisungsproblem mit linear_sum_assignment lösen.

>>> from scipy.optimize import linear_sum_assignment
>>> row_ind, col_ind = linear_sum_assignment(cost)

Die row_ind und col_ind sind optimale zugewiesene Matrixindizes der Kostenmatrix.

>>> row_ind
array([0, 1, 2, 3])
>>> col_ind
array([0, 2, 3, 1])

Die optimale Zuweisung ist

>>> styles = np.array(["backstroke", "breaststroke", "butterfly", "freestyle"])[row_ind]
>>> students = np.array(["A", "B", "C", "D", "E"])[col_ind]
>>> dict(zip(styles, students))
{'backstroke': 'A', 'breaststroke': 'C', 'butterfly': 'D', 'freestyle': 'B'}

Die optimale Gesamt-Medley-Zeit ist

>>> cost[row_ind, col_ind].sum()
163.89999999999998

Beachten Sie, dass dieses Ergebnis nicht dasselbe ist wie die Summe der minimalen Zeiten für jeden Schwimmstil.

>>> np.min(cost, axis=1).sum()
161.39999999999998

da Schüler „C“ sowohl im „Brustschwimmen“ als auch im „Schmetterlingsstil“ der beste Schwimmer ist. Wir können Schüler „C“ nicht beiden Stilen zuweisen, daher haben wir Schüler C dem „Brustschwimmen“-Stil und D dem „Schmetterlingsstil“ zugewiesen, um die Gesamtzeit zu minimieren.

Referenzen

Einige weiterführende Lektüren und verwandte Software, wie Newton-Krylov [KK], PETSc [PP] und PyAMG [AMG].

[KK]

D.A. Knoll und D.E. Keyes, „Jacobian-free Newton-Krylov methods“, J. Comp. Phys. 193, 357 (2004). DOI:10.1016/j.jcp.2003.08.010

[PP]

PETSc https://www.mcs.anl.gov/petsc/ und seine Python-Bindungen https://bitbucket.org/petsc/petsc4py/.

[AMG]

PyAMG (algebraische Mehrgitter-Präkonditionierer/Löser) pyamg/pyamg#issues

Gemischte ganzzahlige lineare Programmierung

Rucksackproblem-Beispiel

Das Rucksackproblem ist ein bekanntes kombinatorisches Optimierungsproblem. Angenommen, wir haben eine Menge von Gegenständen, von denen jeder eine Größe und einen Wert hat, dann besteht das Problem darin, die Gegenstände so auszuwählen, dass der Gesamtwert maximiert wird, unter der Bedingung, dass die Gesamtgröße einen bestimmten Schwellenwert nicht überschreitet.

Formal sei

• \(x_i\) eine boolesche Variable, die angibt, ob Gegenstand \(i\) in den Rucksack aufgenommen wird,

• \(n\) die Gesamtzahl der Gegenstände,

• \(v_i\) der Wert von Gegenstand \(i\),

• \(s_i\) die Größe von Gegenstand \(i\) und

• \(C\) die Kapazität des Rucksacks.

Dann ist das Problem:

\[\max \sum_i^n v_{i} x_{i}\]

\[\text{unter der Bedingung} \sum_i^n s_{i} x_{i} \leq C, x_{i} \in {0, 1}\]

Obwohl die Zielfunktion und die Ungleichheitsnebenbedingungen linear in den *Entscheidungsvariablen* \(x_i\) sind, unterscheidet sich dies von einem typischen linearen Programmierproblem dadurch, dass die Entscheidungsvariablen nur ganzzahlige Werte annehmen können. Insbesondere können unsere Entscheidungsvariablen nur \(0\) oder \(1\) sein, daher ist dies als *binäres ganzzahliges lineares Programm* (BILP) bekannt. Ein solches Problem fällt in die größere Klasse der *gemischten ganzzahligen linearen Programme* (MILPs), die wir mit milp lösen können.

In unserem Beispiel gibt es 8 zur Auswahl stehende Gegenstände, und Größe und Wert jedes einzelnen sind wie folgt angegeben.

>>> import numpy as np
>>> from scipy import optimize
>>> sizes = np.array([21, 11, 15, 9, 34, 25, 41, 52])
>>> values = np.array([22, 12, 16, 10, 35, 26, 42, 53])

Wir müssen unsere acht Entscheidungsvariablen auf binär beschränken. Dies tun wir, indem wir eine Bounds-Beschränkung hinzufügen, um sicherzustellen, dass sie zwischen \(0\) und \(1\) liegen, und wir wenden „Ganzzahligkeitsbeschränkungen“ an, um sicherzustellen, dass sie *entweder* \(0\) *oder* \(1\) sind.

>>> bounds = optimize.Bounds(0, 1)  # 0 <= x_i <= 1
>>> integrality = np.full_like(values, True)  # x_i are integers

Die Rucksackkapazitätsbeschränkung wird mit LinearConstraint angegeben.

>>> capacity = 100
>>> constraints = optimize.LinearConstraint(A=sizes, lb=0, ub=capacity)

Wenn wir den üblichen Regeln der linearen Algebra folgen, sollte die Eingabe A eine zweidimensionale Matrix sein, und die unteren und oberen Schranken lb und ub sollten eindimensionale Vektoren sein, aber LinearConstraint ist nachgiebig, solange die Eingaben auf konsistente Formen übertragen werden können.

Unter Verwendung der oben definierten Variablen können wir das Rucksackproblem mit milp lösen. Beachten Sie, dass milp die Zielfunktion minimiert, wir aber den Gesamtwert maximieren wollen, daher setzen wir c auf das Negative der Werte.

>>> from scipy.optimize import milp
>>> res = milp(c=-values, constraints=constraints,
...            integrality=integrality, bounds=bounds)

Überprüfen wir das Ergebnis.

>>> res.success
True
>>> res.x
array([1., 1., 0., 1., 1., 1., 0., 0.])

Dies bedeutet, dass wir die Gegenstände 1, 2, 4, 5, 6 auswählen sollten, um den Gesamtwert unter der Größenbeschränkung zu optimieren. Beachten Sie, dass dies von dem abweicht, was wir erhalten hätten, wenn wir die *lineare Relaxierung* (ohne Ganzzahligkeitsbeschränkungen) gelöst und versucht hätten, die Entscheidungsvariablen zu runden.

>>> from scipy.optimize import milp
>>> res = milp(c=-values, constraints=constraints,
...            integrality=False, bounds=bounds)
>>> res.x
array([1.        , 1.        , 1.        , 1.        ,
       0.55882353, 1.        , 0.        , 0.        ])

Wenn wir diese Lösung auf array([1., 1., 1., 1., 1., 1., 0., 0.]) aufrunden würden, würde unser Rucksack die Kapazitätsbeschränkung überschreiten, während wir, wenn wir auf array([1., 1., 1., 1., 0., 1., 0., 0.]) abrunden würden, eine suboptimale Lösung hätten.

Weitere MILP-Tutorials finden Sie in den Jupyter-Notebooks auf SciPy Cookbooks.

• Kompression-Sensing L1-Programm

• Kompression-Sensing L0-Programm

Unterstützung für parallele Ausführung

Einige SciPy-Optimierungsmethoden, wie z. B. differential_evolution, bieten Parallelisierung durch die Verwendung eines workers-Schlüsselworts.

Für differential_evolution gibt es zwei Schleifen (Iterationen) auf der Algorithmusebene. Die äußere Schleife repräsentiert aufeinanderfolgende Generationen einer Population. Diese Schleife kann nicht parallelisiert werden. Für eine gegebene Generation müssen Kandidatenlösungen generiert werden, die mit bestehenden Populationsmitgliedern verglichen werden. Die Fitness der Kandidatenlösung kann in einer Schleife erfolgen, aber es ist auch möglich, die Berechnung zu parallelisieren.

Parallelisierung ist auch in anderen Optimierungsalgorithmen möglich. Beispielsweise wird bei verschiedenen minimize-Methoden numerische Differenzierung zur Schätzung von Ableitungen verwendet. Für eine einfache Gradientenberechnung mit zweipunktigen Vorwärtsdifferenzen müssen insgesamt N + 1 Zielfunktionsberechnungen durchgeführt werden, wobei N die Anzahl der Parameter ist. Dies sind nur kleine Störungen um einen gegebenen Punkt (das +1). Diese N + 1 Berechnungen sind ebenfalls parallelisierbar. Die Berechnung numerischer Ableitungen wird vom Minimierungsalgorithmus verwendet, um neue Schritte zu generieren.

Jeder Optimierungsalgorithmus funktioniert auf unterschiedliche Weise, aber sie haben oft Stellen, an denen mehrere Zielfunktionsberechnungen erforderlich sind, bevor der Algorithmus etwas anderes tut. Diese Stellen sind das, was parallelisiert werden kann. Es gibt daher gemeinsame Merkmale, wie workers verwendet wird. Diese Gemeinsamkeiten werden im Folgenden beschrieben.

Wenn eine Ganzzahl angegeben wird, wird ein multiprocessing.Pool erstellt, dessen map-Methode verwendet wird, um Lösungen parallel auszuwerten. Mit diesem Ansatz ist es zwingend erforderlich, dass die Zielfunktion serialisierbar (pickleable) ist. Lambda-Funktionen erfüllen diese Anforderung nicht.

>>> import numpy as np
>>> from scipy.optimize import rosen, differential_evolution, Bounds
>>> bnds = Bounds([0., 0., 0.], [10., 10., 10.])
>>> res = differential_evolution(rosen, bnds, workers=2, updating='deferred')

Es ist auch möglich, eine aufrufbar-ähnliche Map-Funktion als Worker zu verwenden. Hier wird der Map-ähnlichen Funktion eine Reihe von Vektoren übergeben, die der Optimierungsalgorithmus bereitstellt. Die Map-ähnliche Funktion muss jeden Vektor anhand der Zielfunktion auswerten. Im folgenden Beispiel verwenden wir multiprocessing.Pool als Map-ähnliches Objekt. Wie zuvor muss die Zielfunktion immer noch serialisierbar sein. Dieses Beispiel ist semantisch identisch mit dem vorherigen Beispiel.

>>> from multiprocessing import Pool
>>> with Pool(2) as pwl:
...     res = differential_evolution(rosen, bnds, workers=pwl.map, updating='deferred')

Es kann vorteilhaft sein, dieses Muster zu verwenden, da der Pool für weitere Berechnungen wiederverwendet werden kann – die Erstellung dieser Objekte ist mit erheblichem Aufwand verbunden. Alternativen zu multiprocessing.Pool sind das Paket mpi4py, das parallele Verarbeitung auf Clustern ermöglicht.

In Scipy 1.16.0 wurde das Schlüsselwort workers für ausgewählte minimize-Methoden eingeführt. Hier wird die Parallelisierung typischerweise während der numerischen Differenzierung angewendet. Beide oben beschriebenen Ansätze können verwendet werden, es wird jedoch dringend empfohlen, die Map-ähnliche aufrufbar zu übergeben, da die Erstellung neuer Prozesse mit Aufwand verbunden ist. Leistungsgewinne werden nur erzielt, wenn die Zielfunktion teuer zu berechnen ist. Vergleichen wir, wie viel Parallelisierung im Vergleich zur seriellen Version helfen kann. Um eine langsame Funktion zu simulieren, verwenden wir das Paket time.

>>> import time
>>> def slow_func(x):
...     time.sleep(0.0002)
...     return rosen(x)

Untersuchen Sie zuerst die serielle Minimierung.

In [1]: rng = np.random.default_rng()

In [2]: x0 = rng.uniform(low=0.0, high=10.0, size=(20,))

In [3]: %timeit minimize(slow_func, x0, method='L-BFGS-B')  # serial approach
365 ms ± 6.17 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)  # may vary

Nun die parallele Version.

In [4]: with Pool() as pwl:  # parallel approach
...         %timeit minimize(slow_func, x0, method='L-BFGS-B', options={'workers':pwl.map})
70.5 ms ± 146 μs per loop (mean ± std. dev. of 7 runs, 1 loop each)  # may vary

Wenn die Zielfunktion vektorisiert werden kann, kann eine Map-ähnliche Funktion verwendet werden, um die Vektorisierung bei der Funktionsauswertung zu nutzen. Vektorisierung bedeutet, dass die Zielfunktion die erforderlichen Berechnungen in einem einzigen (anstatt mehreren) Aufruf durchführen kann, was typischerweise sehr effizient ist.

In [5]: def vectorized_maplike(fun, iterable):
...         arr = np.array([i for i in iter(iterable)])   # arr.shape = (S, N)
...         arr_t = arr.T                                 # arr_t.shape = (N, S)
...         r = slow_func(arr_t)                          # calculation vectorized over S
...         return r

In [6]: %timeit minimize(slow_func, x0, method='L-BFGS-B', options={'workers':vectorized_maplike})
38.9 ms ± 734 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)  # may vary

Es gibt mehrere wichtige Punkte, die bei diesem Beispiel zu beachten sind.

• Das Iterable repräsentiert die Reihe von Parametervektoren, die der Algorithmus ausgewertet haben möchte.

• Das Iterable wird zunächst in einen Iterator konvertiert, bevor es über eine Listen-Komprehension in ein Array umgewandelt wird. Dies ermöglicht es, dass das Iterable ein Generator, eine Liste, ein Array usw. sein kann.

• Innerhalb der Map-ähnlichen Funktion wird die Berechnung mit slow_func anstelle von fun durchgeführt. Die Map-ähnliche Funktion wird tatsächlich mit einer verpackten Version der Zielfunktion bereitgestellt. Die Verpackung wird verwendet, um verschiedene Arten von häufigen Benutzerfehlern zu erkennen, einschließlich der Überprüfung, ob die Zielfunktion einen Skalar zurückgibt. Wenn fun verwendet wird, führt dies zu einem RuntimeError, da fun(arr_t) ein 1D-Array und kein Skalar ist. Wir verwenden daher slow_func direkt.

• arr.T wird an die Zielfunktion übergeben. Dies liegt daran, dass arr.shape == (S, N) ist, wobei S die Anzahl der auszuwertenden Parametervektoren und N die Anzahl der Variablen ist. Für slow_func tritt Vektorisierung bei Arrays der Form (N, S) auf.

• Dieser Ansatz ist für differential_evolution nicht erforderlich, da dieser Minimierer bereits ein Schlüsselwort für die Vektorisierung besitzt.