scipy.signal.ShortTimeFFT.

from_dual

classmethod ShortTimeFFT.from_dual(dual_win, hop, fs, *, fft_mode='onesided', mfft=None, scale_to=None, phase_shift=0)

Instanziiert ein ShortTimeFFT, indem nur ein Dualfenster angegeben wird.

Wenn eine STFT invertierbar ist, ist es möglich, das Fenster win aus einem gegebenen Dualfenster dual_win zu berechnen. Alle anderen Parameter haben die gleiche Bedeutung wie im Initialisierer von ShortTimeFFT.

Wie im Abschnitt Short-Time Fourier Transform des SciPy User Guide erläutert, kann eine invertierbare STFT als Reihenentwicklung von zeitverschobenen und frequenzmodulierten Dualfenstern interpretiert werden. Z. B. gehört der Reihenkoeffizient S[q,p] zu dem Term, der dual_win um p * delta_t verschoben und mit exp( 2 * j * pi * t * q * delta_f) multipliziert hat.

Siehe auch

from_window

Instanz durch Umschließen von get_window erstellen.

ShortTimeFFT

Instanz über den Standardinitialisierer erstellen.

Beispiele

Probieren Sie es in Ihrem Browser aus!

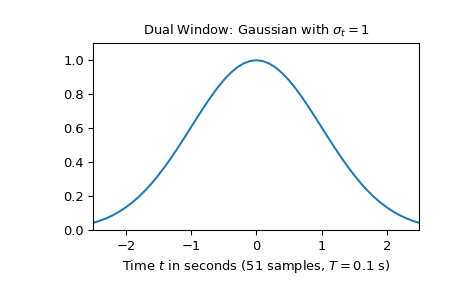
Das folgende Beispiel behandelt die Zerlegung eines Signals in zeit- und frequenzverschobene Gauß-Funktionen. Eine Gauß-Funktion mit einer Standardabweichung von eins, die aus 51 Samples besteht, wird verwendet

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T, N = 0.1, 51
>>> d_win = gaussian(N, std=1/T, sym=True)  # symmetric Gaussian window
>>> t = T * (np.arange(N) - N//2)
...
>>> fg1, ax1 = plt.subplots()
>>> ax1.set_title(r"Dual Window: Gaussian with $\sigma_t=1$")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...        xlim=(t[0], t[-1]), ylim=(0, 1.1*np.max(d_win)))
>>> ax1.plot(t, d_win, 'C0-')

Die folgende Darstellung mit der Überlappung von 41, 11 und 2 Samples zeigt, wie das hop-Intervall die Form des Fensters win beeinflusst

>>> fig2, axx = plt.subplots(3, 1, sharex='all')
...
>>> axx[0].set_title(r"Windows for hop$\in\{10, 40, 49\}$")
>>> for c_, h_ in enumerate([10, 40, 49]):
...     SFT = ShortTimeFFT.from_dual(d_win, h_, 1/T)
...     axx[c_].plot(t + h_ * T, SFT.win, 'k--', alpha=.3, label=None)
...     axx[c_].plot(t - h_ * T, SFT.win, 'k:', alpha=.3, label=None)
...     axx[c_].plot(t, SFT.win, f'C{c_+1}',
...                     label=r"$\Delta t=%0.1f\,$s" % SFT.delta_t)
...     axx[c_].set_ylim(0, 1.1*max(SFT.win))
...     axx[c_].legend(loc='center')
>>> axx[-1].set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...             xlim=(t[0], t[-1]))
>>> plt.show()

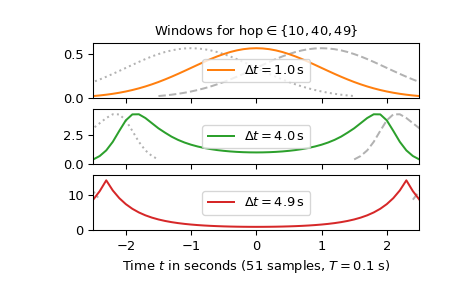
Neben dem Fenster win, das bei t = 0 zentriert ist, sind das vorherige (t = -delta_t) und das nachfolgende Fenster (t = delta_t) dargestellt. Man erkennt, dass bei kleinen hop-Intervallen das Fenster kompakt und glatt ist und eine gute Zeit-Frequenz-Konzentration in der STFT aufweist. Für das große hop-Intervall von 4,9 s hat das Fenster kleine Werte um t = 0, die nicht von der Überlappung der benachbarten Fenster abgedeckt werden, was zu numerischen Ungenauigkeiten führen kann. Darüber hinaus deutet die spitze Form am Anfang und Ende des Fensters auf eine höhere Bandbreite hin, was zu einer schlechteren Zeit-Frequenz-Auflösung der STFT führt. Daher wird die Wahl des hop-Intervalls ein Kompromiss zwischen der Zeit-Frequenz-Auflösung und den Speicheranforderungen sein, die durch kleine hop-Größen bedingt sind.

ZurückIn Tab öffnen