scipy.signal.

gammatone

scipy.signal.gammatone(freq, ftype, order=None, numtaps=None, fs=None)

Design eines Gammatone-Filters.

Diese Funktion berechnet die Koeffizienten eines FIR- oder IIR-Gammatone-Digitalfilters [1].

Parameter:

freqfloat

Mittenfrequenz des Filters (ausgedrückt in denselben Einheiten wie fs).

ftype{‘fir’, ‘iir’}

Der Typ des vom Funktionen generierten Filters. Wenn ‘fir’, generiert die Funktion einen FIR-Gammatone-Filter n-ter Ordnung. Wenn ‘iir’, generiert die Funktion einen digitalen IIR-Filter 8. Ordnung, der als Gammatone-Filter 4. Ordnung modelliert ist.

orderint, optional

Die Ordnung des Filters. Wird nur verwendet, wenn ftype='fir'. Standard ist 4 zur Modellierung des menschlichen auditorischen Systems. Muss zwischen 0 und 24 liegen.

numtapsint, optional

Länge des Filters. Wird nur verwendet, wenn ftype='fir'. Standard ist fs*0.015, wenn fs größer als 1000 ist, und 15, wenn fs kleiner oder gleich 1000 ist.

fsfloat, optional

Die Abtastfrequenz des Signals. freq muss zwischen 0 und fs/2 liegen. Standard ist 2.

Rückgabe:

b, andarray, ndarray

Zählerpolynom (b) und Nennerpolynom (a) des Filters.

Löst aus:

ValueError

Wenn freq kleiner oder gleich 0 oder größer oder gleich fs/2 ist, wenn ftype nicht ‘fir’ oder ‘iir’ ist, wenn order kleiner oder gleich 0 oder größer als 24 ist, wenn ftype='fir'

Siehe auch

firwin

iirfilter

Referenzen

[1]

Slaney, Malcolm, „An Efficient Implementation of the Patterson-Holdsworth Auditory Filter Bank“, Apple Computer Technical Report 35, 1993, S. 3-8, 34-39.

Beispiele

Probieren Sie es in Ihrem Browser aus!

16-Tap FIR Gammatone-Filter 4. Ordnung, zentriert bei 440 Hz

>>> from scipy import signal
>>> signal.gammatone(440, 'fir', numtaps=16, fs=16000)
(array([ 0.00000000e+00,  2.22196719e-07,  1.64942101e-06,  4.99298227e-06,
    1.01993969e-05,  1.63125770e-05,  2.14648940e-05,  2.29947263e-05,
    1.76776931e-05,  2.04980537e-06, -2.72062858e-05, -7.28455299e-05,
   -1.36651076e-04, -2.19066855e-04, -3.18905076e-04, -4.33156712e-04]),
   [1.0])

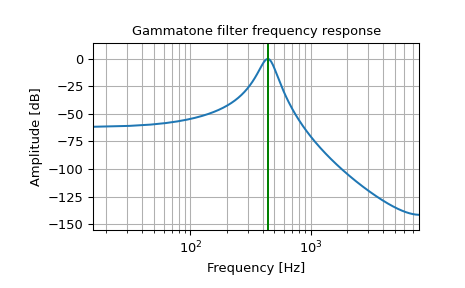
IIR Gammatone-Filter, zentriert bei 440 Hz

>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> fc, fs = 440, 16000
>>> b, a = signal.gammatone(fc, 'iir', fs=fs)
>>> w, h = signal.freqz(b, a)
>>> plt.plot(w * fs / (2 * np.pi), 20 * np.log10(abs(h)))
>>> plt.xscale('log')
>>> plt.title('Gammatone filter frequency response')
>>> plt.xlabel('Frequency [Hz]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(fc, color='green') # cutoff frequency
>>> plt.show()

ZurückIn Tab öffnen