scipy.signal.

iirfilter#

scipy.signal.iirfilter(N, Wn, rp=None, rs=None, btype='band', analog=False, ftype='butter', output='ba', fs=None)[Quelle]#

IIR-Filterdesign für digitale und analoge Filter anhand von Ordnung und kritischen Punkten.

Entwirft einen digitalen oder analogen Filter der Ordnung N und gibt die Filterkoeffizienten zurück.

Parameter:
Nint

Die Ordnung des Filters.

Wnarray_like

Eine Skalar oder eine Sequenz der Länge 2, die die kritischen Frequenzen angibt.

Für digitale Filter sind Wn in derselben Einheit wie fs angegeben. Standardmäßig ist fs 2 Halbzyklen/Sample, daher sind diese von 0 bis 1 normalisiert, wobei 1 die Nyquist-Frequenz ist. (Wn sind somit in Halbzyklen / Sample.)

Für analoge Filter ist Wn eine Winkelfrequenz (z. B. rad/s).

Wenn Wn eine Sequenz der Länge 2 ist, muss Wn[0] kleiner als Wn[1] sein.

rpfloat, optional

Für Tschebyscheff- und Elliptische Filter gibt dies die maximale Welligkeit im Durchlassbereich an. (dB)

rsfloat, optional

Für Tschebyscheff- und Elliptische Filter gibt dies die minimale Dämpfung im Sperrbereich an. (dB)

btype{‘bandpass’, ‘lowpass’, ‘highpass’, ‘bandstop’}, optional

Der Filtertyp. Standard ist 'bandpass'.

analogbool, optional

Wenn True, wird ein analoger Filter zurückgegeben, andernfalls ein digitaler Filter.

ftypestr, optional

Der Typ des zu entwerfenden IIR-Filters

  • Butterworth : ‘butter’

  • Tschebyscheff I : ‘cheby1’

  • Tschebyscheff II : ‘cheby2’

  • Cauer/Elliptisch: ‘ellip’

  • Bessel/Thomson: ‘bessel’

output{‘ba’, ‘zpk’, ‘sos’}, optional

Filterform der Ausgabe

  • Zweite-Ordnung-Abschnitte (empfohlen): ‘sos’

  • Zähler/Nenner (Standard): ‘ba’

  • Pol-Nullstelle : ‘zpk’

Im Allgemeinen wird die Form der zweite-Ordnung-Abschnitte (‘sos’) empfohlen, da die Ableitung der Koeffizienten für die Zähler/Nenner-Form (‘ba’) numerischen Instabilitäten unterliegt. Aus Gründen der Abwärtskompatibilität ist die Standardform die Zähler/Nenner-Form (‘ba’), wobei sich das ‚b‘ und das ‚a‘ in ‚ba‘ auf die üblicherweise verwendeten Namen der Koeffizienten beziehen.

Hinweis: Die Verwendung der zweite-Ordnung-Abschnitte-Form (‘sos’) ist manchmal mit zusätzlichen Rechenkosten verbunden: Für datenintensive Anwendungsfälle wird daher empfohlen, auch die Zähler/Nenner-Form (‘ba’) zu untersuchen.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems.

Hinzugefügt in Version 1.2.0.

Rückgabe:
b, andarray, ndarray

Zähler- (b) und Nenner- (a) Polynome des IIR-Filters. Nur zurückgegeben, wenn output='ba'.

z, p, kndarray, ndarray, float

Nullstellen, Pole und Systemverstärkung der Übertragungsfunktion des IIR-Filters. Nur zurückgegeben, wenn output='zpk'.

sosndarray

Zweistufige Abschnittsdarstellung des IIR-Filters. Nur zurückgegeben, wenn output='sos'.

Siehe auch

butter

Filterentwurf unter Verwendung von Ordnung und kritischen Punkten

cheby1, cheby2, ellip, bessel
buttord

Ordnung und kritische Punkte aus Durchlass- und Sperrbereichsspezifikationen ermitteln

cheb1ord, cheb2ord, ellipord
iirdesign

Allgemeines Filterdesign mit Spezifikationen für Durchlass- und Sperrbereich

Hinweise

Der Parameter output='sos' wurde in 0.16.0 hinzugefügt.

Beispiele

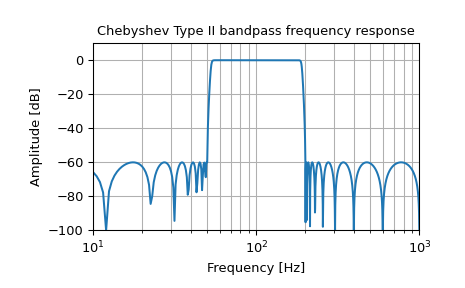
Generiert einen Tschebyscheff II Analog-Bandpassfilter der 17. Ordnung zwischen 50 Hz und 200 Hz und plottet die Frequenzantwort.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirfilter(17, [2*np.pi*50, 2*np.pi*200], rs=60,
...                         btype='band', analog=True, ftype='cheby2')
>>> w, h = signal.freqs(b, a, 1000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1)
>>> ax.semilogx(w / (2*np.pi), 20 * np.log10(np.maximum(abs(h), 1e-5)))
>>> ax.set_title('Chebyshev Type II bandpass frequency response')
>>> ax.set_xlabel('Frequency [Hz]')
>>> ax.set_ylabel('Amplitude [dB]')
>>> ax.axis((10, 1000, -100, 10))
>>> ax.grid(which='both', axis='both')
>>> plt.show()
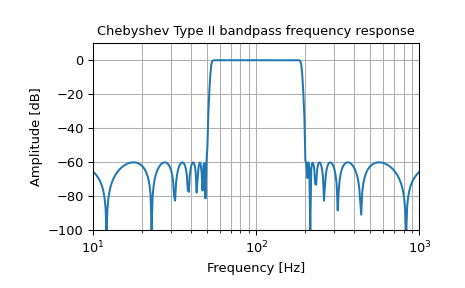
../../_images/scipy-signal-iirfilter-1_00_00.png

Erstellt einen digitalen Filter mit denselben Eigenschaften in einem System mit einer Abtastrate von 2000 Hz und plottet die Frequenzantwort. (Die Implementierung mit zweite-Ordnung-Abschnitten ist erforderlich, um die Stabilität eines Filters dieser Ordnung zu gewährleisten)

>>> sos = signal.iirfilter(17, [50, 200], rs=60, btype='band',
...                        analog=False, ftype='cheby2', fs=2000,
...                        output='sos')
>>> w, h = signal.freqz_sos(sos, 2000, fs=2000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1)
>>> ax.semilogx(w, 20 * np.log10(np.maximum(abs(h), 1e-5)))
>>> ax.set_title('Chebyshev Type II bandpass frequency response')
>>> ax.set_xlabel('Frequency [Hz]')
>>> ax.set_ylabel('Amplitude [dB]')
>>> ax.axis((10, 1000, -100, 10))
>>> ax.grid(which='both', axis='both')
>>> plt.show()
../../_images/scipy-signal-iirfilter-1_01_00.png
Auf dieser Seite