scipy.signal.

stft#

scipy.signal.stft(x, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, boundary='zeros', padded=True, axis=-1, scaling='spectrum')[Quelle]#

Berechnet die Short Time Fourier Transform (Legacy-Funktion).

STFTs können verwendet werden, um die Veränderung des Frequenz- und Phaseninhalts eines nichtstationären Signals über die Zeit zu quantifizieren.

Veraltet

Diese Funktion gilt als Legacy und wird keine Updates mehr erhalten. Obwohl wir derzeit keine Pläne haben, sie zu entfernen, empfehlen wir, dass neuer Code modernere Alternativen verwendet. ShortTimeFFT ist eine neuere STFT / ISTFT-Implementierung mit mehr Funktionen. Ein Vergleich zwischen den Implementierungen finden Sie im Abschnitt Short-Time Fourier Transform des SciPy User Guide.

Parameter:

xarray_like: Zeitreihen von Messwerten
fsfloat, optional: Abtastfrequenz der Zeitreihe x. Standardwert ist 1.0.
windowstr oder Tupel oder Array_like, optional: Gewünschtes Fenster zur Verwendung. Wenn window eine Zeichenkette oder ein Tupel ist, wird es an get_window übergeben, um die Fensterwerte zu generieren, die standardmäßig DFT-gerade sind. Siehe get_window für eine Liste von Fenstern und erforderliche Parameter. Wenn window Array_like ist, wird es direkt als Fenster verwendet und seine Länge muss nperseg sein. Standard ist ein Hann-Fenster.
npersegint, optional: Länge jedes Segments. Standardwert ist 256.
noverlapint, optional: Anzahl der Punkte, die zwischen den Segmenten überlappen. Wenn None, dann noverlap = nperseg // 2. Standardwert ist None. Wenn angegeben, muss die COLA-Bedingung erfüllt sein (siehe Hinweise unten).
nfftint, optional: Länge der FFT, die verwendet wird, wenn eine Null-gepolsterte FFT gewünscht wird. Wenn None, ist die FFT-Länge nperseg. Standard ist None.
detrendstr oder Funktion oder False, optional: Gibt an, wie jedes Segment entzerrt werden soll. Wenn detrend ein String ist, wird er als type-Argument an die Funktion detrend übergeben. Wenn es eine Funktion ist, nimmt sie ein Segment und gibt ein entzerrtes Segment zurück. Wenn detrend False ist, wird keine Entzerrung durchgeführt. Standardwert ist False.
return_onesidedbool, optional: Wenn True, wird ein einseitiges Spektrum für reale Daten zurückgegeben. Wenn False, wird ein zweiseitiges Spektrum zurückgegeben. Standard ist True, aber für komplexe Daten wird immer ein zweiseitiges Spektrum zurückgegeben.
boundarystr oder None, optional: Gibt an, ob das Eingabesignal an beiden Enden erweitert wird und wie die neuen Werte generiert werden, um das erste Fenstersegment am ersten Eingabepunkt zu zentrieren. Dies hat den Vorteil, dass der erste Eingabepunkt rekonstruiert werden kann, wenn die verwendete Fensterfunktion bei Null beginnt. Gültige Optionen sind ['even', 'odd', 'constant', 'zeros', None]. Standard ist 'zeros' für eine Erweiterung mit Nullauffüllung. D.h. [1, 2, 3, 4] wird zu [0, 1, 2, 3, 4, 0] für nperseg=3 erweitert.
paddedbool, optional: Gibt an, ob das Eingabesignal am Ende mit Nullen aufgefüllt wird, damit das Signal genau in eine ganze Anzahl von Fenstersegmenten passt, sodass das gesamte Signal in die Ausgabe einbezogen wird. Standardwert ist True. Die Auffüllung erfolgt nach der Randverlängerung, wenn boundary nicht None ist und padded True ist, was dem Standard entspricht.
axisint, optional: Achse, entlang derer die STFT berechnet wird; Standard ist die letzte Achse (d.h. axis=-1).
scaling: {‘spectrum’, ‘psd’}: Die Standardeinstellung 'spectrum' ermöglicht es, jede Frequenzlinie von Zxx als Magnitudenspektrum zu interpretieren. Die Option 'psd' skaliert jede Linie auf eine Leistungsdichtespektrum – sie ermöglicht die Berechnung der Energie des Signals durch numerische Integration von abs(Zxx)**2.

Hinzugefügt in Version 1.9.0.

Rückgabe:

fndarray: Array von Abtastfrequenzen.
tndarray: Array von Segmentzeiten.
Zxxndarray: STFT von x. Standardmäßig entspricht die letzte Achse von Zxx den Segmentzeiten.

Siehe auch

istft: Inverse Short Time Fourier Transform
ShortTimeFFT: Neuere STFT/ISTFT-Implementierung mit mehr Funktionen.
check_COLA: Prüft, ob die Constant OverLap Add (COLA) Bedingung erfüllt ist.
check_NOLA: Prüft, ob die Nicht-Null-Überlappungs-Additions- (NOLA) Bedingung erfüllt ist
welch: Leistungsdichteschätzung nach der Welch-Methode.
spectrogram: Spektrogramm nach der Welch-Methode.
csd: Kreuzspektraldichteschätzung nach der Welch-Methode.
lombscargle: Lomb-Scargle-Periodogramm für ungleichmäßig abgetastete Daten

Hinweise

Um eine STFT über die inverse STFT in istft invertieren zu können, muss die Signalwindowing die Bedingung "Nonzero OverLap Add" (NOLA) erfüllen und das Eingangssignal muss eine vollständige Windowing-Abdeckung aufweisen (d.h. (x.shape[axis] - nperseg) % (nperseg-noverlap) == 0). Das Argument padded kann verwendet werden, um dies zu erreichen.

Gegeben sei ein zeitorientiertes Signal \(x[n]\), ein Fenster \(w[n]\) und eine Schrittgröße \(H\) = nperseg - noverlap. Der Fensterrahmen zum Zeitpunktindex \(t\) ist gegeben durch

\[x_{t}[n]=x[n]w[n-tH]\]

Die Überlappungs-Additions- (OLA) Rekonstruktionsgleichung ist gegeben durch

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

Die NOLA-Bedingung stellt sicher, dass jeder Nennerterm in der OLA-Rekonstruktionsgleichung nicht null ist. Ob eine Wahl von window, nperseg und noverlap diese Bedingung erfüllt, kann mit check_NOLA getestet werden.

Hinzugefügt in Version 0.19.0.

Referenzen

[1]

Oppenheim, Alan V., Ronald W. Schafer, John R. Buck „Discrete-Time Signal Processing“, Prentice Hall, 1999.

[2]

Daniel W. Griffin, Jae S. Lim „Signal Estimation from Modified Short-Time Fourier Transform“, IEEE 1984, 10.1109/TASSP.1984.1164317

Beispiele

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

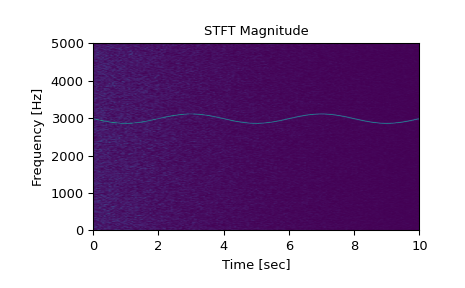
Generiert ein Testsignal, eine Sinuswelle mit 2 Veff, deren Frequenz langsam um 3 kHz moduliert wird, korrumpiert durch weißes Rauschen mit exponentiell abnehmender Amplitude, abgetastet mit 10 kHz.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.01 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> mod = 500*np.cos(2*np.pi*0.25*time)
>>> carrier = amp * np.sin(2*np.pi*3e3*time + mod)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> noise *= np.exp(-time/5)
>>> x = carrier + noise

Berechnet und plottet die Magnitude der STFT.

>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000)
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()

../../_images/scipy-signal-stft-1_00_00.png

Vergleicht die Energie des Signals x mit der Energie seiner STFT

>>> E_x = sum(x**2) / fs  # Energy of x
>>> # Calculate a two-sided STFT with PSD scaling:
>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000, return_onesided=False,
...                         scaling='psd')
>>> # Integrate numerically over abs(Zxx)**2:
>>> df, dt = f[1] - f[0], t[1] - t[0]
>>> E_Zxx = sum(np.sum(Zxx.real**2 + Zxx.imag**2, axis=0) * df) * dt
>>> # The energy is the same, but the numerical errors are quite large:
>>> np.isclose(E_x, E_Zxx, rtol=1e-2)
True