scipy.special.i0#

scipy.special.i0(x, out=None) = <ufunc 'i0'>#

Modifizierte Besselfunktion der Ordnung 0.

Definiert als,

\[I_0(x) = \sum_{k=0}^\infty \frac{(x^2/4)^k}{(k!)^2} = J_0(\imath x),\]

wobei \(J_0\) die Besselfunktion der ersten Art der Ordnung 0 ist.

Parameter:

xarray_like: Argument (float)
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

ISkalar oder ndarray: Wert der modifizierten Besselfunktion der Ordnung 0 bei x.

Siehe auch

iv: Modifizierte Besselfunktion beliebiger Ordnung
i0e: Exponentiell skalierte modifizierte Besselfunktion der Ordnung 0

Hinweise

Der Bereich wird in die zwei Intervalle [0, 8] und (8, unendlich) aufgeteilt. In jedem Intervall werden Tschebyscheff-Polynom-Entwicklungen verwendet.

Diese Funktion ist ein Wrapper für die Cephes [1] Routine i0.

i0 hat experimentelle Unterstützung für Backends, die dem Python Array API Standard entsprechen, zusätzlich zu NumPy. Bitte erwägen Sie, diese Funktionen zu testen, indem Sie die Umgebungsvariable SCIPY_ARRAY_API=1 setzen und CuPy-, PyTorch-, JAX- oder Dask-Arrays als Array-Argumente übergeben. Die folgenden Kombinationen aus Backend und Gerät (oder anderer Fähigkeit) werden unterstützt.

Bibliothek	CPU	GPU
NumPy	✅	n/a
CuPy	n/a	✅
PyTorch	✅	✅
JAX	✅	✅
Dask	✅	n/a

Siehe Unterstützung für den Array API Standard für weitere Informationen.

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Berechnen Sie die Funktion an einem Punkt

>>> from scipy.special import i0
>>> i0(1.)
1.2660658777520082

Berechnung an mehreren Punkten

>>> import numpy as np
>>> i0(np.array([-2., 0., 3.5]))
array([2.2795853 , 1.        , 7.37820343])

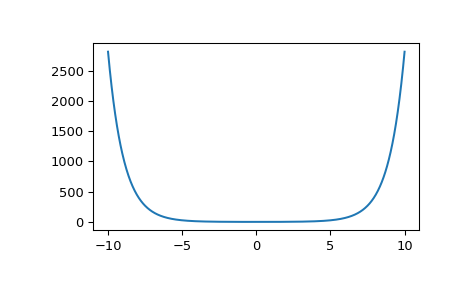
Plotten Sie die Funktion von -10 bis 10.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(-10., 10., 1000)
>>> y = i0(x)
>>> ax.plot(x, y)
>>> plt.show()