scipy.special.iv#

scipy.special.iv(v, z, out=None) = <ufunc 'iv'>#

Modifizierte Besselfunktion der ersten Art von reeller Ordnung.

Parameter:

varray_like: Ordnung. Wenn z vom reellen Typ und negativ ist, muss v ganzzahlig sein.
zarray_like von float oder complex: Argument.
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

skalar oder ndarray: Werte der modifizierten Besselfunktion.

Siehe auch

ive: Diese Funktion, bei der das führende exponentielle Verhalten gestrichen ist.
i0: Schnellere Version dieser Funktion für Ordnung 0.
i1: Schnellere Version dieser Funktion für Ordnung 1.

Hinweise

Für reelles z und \(v \in [-50, 50]\) wird die Auswertung mit Temmes Methode [1] durchgeführt. Für größere Ordnungen werden gleichmäßige asymptotische Entwicklungen angewendet.

Für komplexes z und positives v wird die AMOS [2] Routine zbesi aufgerufen. Sie verwendet eine Potenzreihe für kleines z, die asymptotische Entwicklung für große abs(z), den Miller-Algorithmus normalisiert durch die Wronski-Determinante und eine Neumann-Reihe für mittlere Magnituden sowie die gleichmäßigen asymptotischen Entwicklungen für \(I_v(z)\) und \(J_v(z)\) für große Ordnungen. Rückwärtsrezidiv wird verwendet, um Sequenzen zu erzeugen oder Ordnungen bei Bedarf zu reduzieren.

Die obigen Berechnungen erfolgen in der rechten Halbebene und werden nach der Formel in die linke Halbebene fortgesetzt,

\[I_v(z \exp(\pm\imath\pi)) = \exp(\pm\pi v) I_v(z)\]

(gültig, wenn der Realteil von z positiv ist). Für negatives v gilt die Formel

\[I_{-v}(z) = I_v(z) + \frac{2}{\pi} \sin(\pi v) K_v(z)\]

wobei \(K_v(z)\) die modifizierte Besselfunktion der zweiten Art ist, die mit der AMOS-Routine zbesk ausgewertet wird.

Referenzen

[1]

Temme, Journal of Computational Physics, Bd. 21, 343 (1976)

[2]

Donald E. Amos, „AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order“, http://netlib.org/amos/

Beispiele

Auswertung der Funktion der Ordnung 0 an einem Punkt.

>>> from scipy.special import iv
>>> iv(0, 1.)
1.2660658777520084

Auswertung der Funktion an einem Punkt für verschiedene Ordnungen.

>>> iv(0, 1.), iv(1, 1.), iv(1.5, 1.)
(1.2660658777520084, 0.565159103992485, 0.2935253263474798)

Die Auswertung für verschiedene Ordnungen kann in einem Aufruf erfolgen, indem eine Liste oder ein NumPy-Array als Argument für den Parameter v übergeben wird.

>>> iv([0, 1, 1.5], 1.)
array([1.26606588, 0.5651591 , 0.29352533])

Auswertung der Funktion an mehreren Punkten für Ordnung 0 durch Übergabe eines Arrays für z.

>>> import numpy as np
>>> points = np.array([-2., 0., 3.])
>>> iv(0, points)
array([2.2795853 , 1.        , 4.88079259])

Wenn z ein Array ist, muss der Ordnungs-Parameter v so broadcastfähig sein, dass die korrekte Form entsteht, wenn in einem Aufruf unterschiedliche Ordnungen berechnet werden sollen. Um die Ordnungen 0 und 1 für ein 1D-Array zu berechnen

>>> orders = np.array([[0], [1]])
>>> orders.shape
(2, 1)

>>> iv(orders, points)
array([[ 2.2795853 ,  1.        ,  4.88079259],
       [-1.59063685,  0.        ,  3.95337022]])

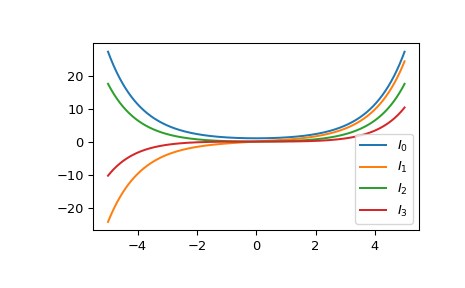
Plotten Sie die Funktionen der Ordnungen 0 bis 3 von -5 bis 5.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(-5., 5., 1000)
>>> for i in range(4):
...     ax.plot(x, iv(i, x), label=f'$I_{i!r}$')
>>> ax.legend()
>>> plt.show()