scipy.special.kve#
- scipy.special.kve(v, z, out=None) = <ufunc 'kve'>#
Exponentiell skalierte modifizierte Besselfunktion der zweiten Art.
Gibt die exponentiell skalierte, modifizierte Besselfunktion der zweiten Art (manchmal auch als dritte Art bezeichnet) für reelle Ordnung v bei komplexen z zurück.
kve(v, z) = kv(v, z) * exp(z)
- Parameter:
- varray_like of float
Ordnung von Besselfunktionen
- zarray_like of complex
Argument, an dem die Besselfunktionen ausgewertet werden sollen
- outndarray, optional
Optionales Ausgabe-Array für die Funktionsergebnisse
- Rückgabe:
- skalar oder ndarray
Die exponentiell skalierte modifizierte Besselfunktion der zweiten Art.
Siehe auch
Hinweise
Wrapper für die AMOS [1] Routine zbesk. Eine Diskussion des verwendeten Algorithmus finden Sie in [2] und den dort genannten Referenzen.
Referenzen
[1]Donald E. Amos, „AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order“, http://netlib.org/amos/
[2]Donald E. Amos, „Algorithm 644: A portable package for Bessel functions of a complex argument and nonnegative order“, ACM TOMS Vol. 12 Issue 3, Sept. 1986, S. 265
Beispiele
Im folgenden Beispiel gibt
kv0 zurück, währendkveimmer noch eine nützliche endliche Zahl zurückgibt.>>> import numpy as np >>> from scipy.special import kv, kve >>> import matplotlib.pyplot as plt >>> kv(3, 1000.), kve(3, 1000.) (0.0, 0.03980696128440973)
Wertet die Funktion an einem Punkt für verschiedene Ordnungen aus, indem eine Liste oder ein NumPy-Array als Argument für den Parameter v übergeben wird.
>>> kve([0, 1, 1.5], 1.) array([1.14446308, 1.63615349, 2.50662827])
Auswertung der Funktion an mehreren Punkten für Ordnung 0 durch Übergabe eines Arrays für z.
>>> points = np.array([1., 3., 10.]) >>> kve(0, points) array([1.14446308, 0.6977616 , 0.39163193])
Wertet die Funktion an mehreren Punkten für verschiedene Ordnungen aus, indem Arrays sowohl für v als auch für z übergeben werden. Beide Arrays müssen broadcastable auf die richtige Form sein. Um die Ordnungen 0, 1 und 2 für ein 1D-Array von Punkten zu berechnen.
>>> kve([[0], [1], [2]], points) array([[1.14446308, 0.6977616 , 0.39163193], [1.63615349, 0.80656348, 0.41076657], [4.41677005, 1.23547058, 0.47378525]])
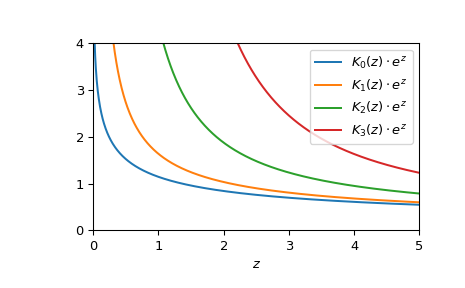
Plotten der Funktionen der Ordnungen 0 bis 3 von 0 bis 5.
>>> fig, ax = plt.subplots() >>> x = np.linspace(0., 5., 1000) >>> for i in range(4): ... ax.plot(x, kve(i, x), label=fr'$K_{i!r}(z)\cdot e^z$') >>> ax.legend() >>> ax.set_xlabel(r"$z$") >>> ax.set_ylim(0, 4) >>> ax.set_xlim(0, 5) >>> plt.show()