scipy.special.j1#
- scipy.special.j1(x, out=None) = <ufunc 'j1'>#
Bessel-Funktion der ersten Art der Ordnung 1.
- Parameter:
- xarray_like
Argument (float).
- outndarray, optional
Optionales Ausgabe-Array für die Funktionswerte
- Rückgabe:
- JSkalar oder ndarray
Wert der Bessel-Funktion der ersten Art der Ordnung 1 an der Stelle x.
Siehe auch
jvBesselfunktion erster Art
spherical_jnSphärische Bessel-Funktionen.
Hinweise
Der Definitionsbereich wird in die Intervalle [0, 8] und (8, unendlich) unterteilt. Im ersten Intervall wird eine Chebyshev-Entwicklung mit 24 Termen verwendet. Im zweiten Intervall wird die asymptotische trigonometrische Darstellung unter Verwendung zweier rationaler Funktionen vom Grad 5/5 eingesetzt.
Diese Funktion ist ein Wrapper für die Cephes-Routine [1]
j1. Sie sollte nicht mit den sphärischen Bessel-Funktionen (siehespherical_jn) verwechselt werden.Referenzen
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Beispiele
Berechnen Sie die Funktion an einem Punkt
>>> from scipy.special import j1 >>> j1(1.) 0.44005058574493355
Berechnung der Funktion an mehreren Punkten
>>> import numpy as np >>> j1(np.array([-2., 0., 4.])) array([-0.57672481, 0. , -0.06604333])
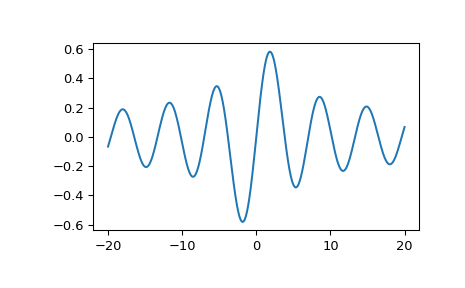
Zeichnen der Funktion von -20 bis 20.
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> x = np.linspace(-20., 20., 1000) >>> y = j1(x) >>> ax.plot(x, y) >>> plt.show()