scipy.special.kn#
- scipy.special.kn(n, x, out=None) = <ufunc 'kn'>#
Modifizierte Besselfunktion zweiter Art ganzzahliger Ordnung n
Gibt die modifizierte Besselfunktion zweiter Art für ganzzahlige Ordnung n für reelle z zurück.
Diese werden manchmal auch als Funktionen dritter Art, Basset-Funktionen oder Macdonald-Funktionen bezeichnet.
- Parameter:
- narray_like von int
Ordnung der Besselfunktionen (Gleitkommazahlen werden mit einer Warnung abgeschnitten)
- xarray_like von float
Argument, an dem die Besselfunktionen ausgewertet werden sollen
- outndarray, optional
Optionales Ausgabearray für die Funktionsergebnisse.
- Rückgabe:
- skalar oder ndarray
Wert der Modifizierten Besselfunktion zweiter Art, \(K_n(x)\).
Siehe auch
Hinweise
Wrapper für die AMOS [1] Routine zbesk. Eine Diskussion des verwendeten Algorithmus finden Sie unter [2] und die dortigen Referenzen.
Referenzen
[1]Donald E. Amos, „AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order“, http://netlib.org/amos/
[2]Donald E. Amos, „Algorithm 644: A portable package for Bessel functions of a complex argument and nonnegative order“, ACM TOMS Vol. 12 Issue 3, Sept. 1986, S. 265
Beispiele
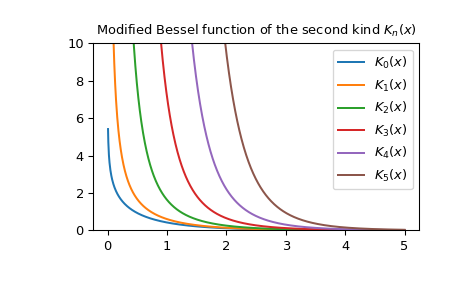
Zeichnen Sie die Funktion mehrerer Ordnungen für reelle Eingaben
>>> import numpy as np >>> from scipy.special import kn >>> import matplotlib.pyplot as plt >>> x = np.linspace(0, 5, 1000) >>> for N in range(6): ... plt.plot(x, kn(N, x), label='$K_{}(x)$'.format(N)) >>> plt.ylim(0, 10) >>> plt.legend() >>> plt.title(r'Modified Bessel function of the second kind $K_n(x)$') >>> plt.show()
Berechnung für einen einzelnen Wert bei mehreren Ordnungen
>>> kn([4, 5, 6], 1) array([ 44.23241585, 360.9605896 , 3653.83831186])