scipy.stats.

power

scipy.stats.power(test, rvs, n_observations, *, significance=0.01, vectorized=None, n_resamples=10000, batch=None, kwargs=None)

Simuliert die Power eines Hypothesentests unter einer alternativen Hypothese.

Parameter:

testcallable

Hypothesentest, dessen Power simuliert werden soll. test muss ein aufrufbares Objekt sein, das eine Stichprobe akzeptiert (z.B. test(sample)) oder len(rvs) separate Stichproben (z.B. test(samples1, sample2), wenn rvs zwei aufrufbare Objekte enthält und n_observations zwei Werte enthält) und den p-Wert des Tests zurückgibt. Wenn vectorized auf True gesetzt ist, muss test auch ein Schlüsselwortargument axis akzeptieren und vektorisiert sein, um den Test entlang der bereitgestellten axis der Stichproben durchzuführen. Jedes aufrufbare Objekt aus scipy.stats mit einem axis-Argument, das ein Objekt mit einem pvalue-Attribut zurückgibt, ist ebenfalls akzeptabel.

rvscallable or tuple of callables

Ein aufrufbares Objekt oder eine Sequenz von aufrufbaren Objekten, die Zufallsvariablen unter der alternativen Hypothese generieren. Jedes Element von rvs muss das Schlüsselwortargument size akzeptieren (z.B. rvs(size=(m, n))) und ein N-dimensionales Array dieser Form zurückgeben. Wenn rvs eine Sequenz ist, muss die Anzahl der aufrufbaren Objekte in rvs mit der Anzahl der Elemente von n_observations übereinstimmen, d.h. len(rvs) == len(n_observations). Wenn rvs ein einzelnes aufrufbares Objekt ist, wird n_observations als einzelnes Element behandelt.

n_observationstuple of ints or tuple of integer arrays

Wenn eine Sequenz von Integern, jede ist die Größe einer Stichprobe, die an test übergeben wird. Wenn eine Sequenz von Integer-Arrays, wird die Power für jeden Satz entsprechender Stichprobengrößen simuliert. Siehe Beispiele.

significancefloat or array_like of floats, default: 0.01

Die Schwelle für die Signifikanz; d.h. der p-Wert, unter dem die Ergebnisse des Hypothesentests als Beweis gegen die Nullhypothese betrachtet werden. Äquivalent dazu ist die akzeptable Rate von Typ-I-Fehlern unter der Nullhypothese. Wenn ein Array, wird die Power für jeden Signifikanzschwellenwert simuliert.

kwargsdict, optional

Schlüsselwortargumente, die an die aufrufbaren Objekte rvs und/oder test übergeben werden. Introspektion wird verwendet, um zu bestimmen, welche Schlüsselwortargumente an jedes aufrufbare Objekt übergeben werden können. Der Wert, der jedem Schlüsselwort zugeordnet ist, muss ein Array sein. Arrays müssen miteinander und mit jedem Array in n_observations broadcastfähig sein. Die Power wird für jeden Satz entsprechender Stichprobengrößen und Argumente simuliert. Siehe Beispiele.

vectorizedbool, optional

Wenn vectorized auf False gesetzt ist, wird test nicht das Schlüsselwortargument axis übergeben und es wird erwartet, dass der Test nur für 1D-Stichproben durchgeführt wird. Wenn True, wird test das Schlüsselwortargument axis übergeben und es wird erwartet, dass der Test entlang der axis durchgeführt wird, wenn N-dimensionale Stichproben-Arrays übergeben werden. Wenn None (Standard), wird vectorized auf True gesetzt, wenn axis ein Parameter von test ist. Die Verwendung eines vektorisierten Tests reduziert typischerweise die Rechenzeit.

n_resamplesint, default: 10000

Anzahl der aus jedem der aufrufbaren Objekte von rvs gezogenen Stichproben. Äquivalent dazu ist die Anzahl der unter der alternativen Hypothese durchgeführten Tests zur Annäherung der Power.

batchint, optional

Die Anzahl der Stichproben, die in jedem Aufruf von test verarbeitet werden sollen. Der Speicherverbrauch ist proportional zum Produkt von batch und der größten Stichprobengröße. Standard ist None, in welchem Fall batch gleich n_resamples ist.

Rückgabe:

resPowerResult

Ein Objekt mit den Attributen

powerfloat or ndarray

Die geschätzte Power gegenüber der Alternative.

pvaluesndarray

Die unter der alternativen Hypothese beobachteten p-Werte.

Hinweise

Die Power wird wie folgt simuliert:

• Zeichne viele Zufallsstichproben (oder Sätze von Stichproben), jede von der/den durch n_observations spezifizierten Größe(n), unter der durch rvs spezifizierten Alternative.

• Berechne für jede Stichprobe (oder jeden Satz von Stichproben) den p-Wert gemäß test. Diese p-Werte werden im Attribut pvalues des Ergebnisobjekts aufgezeichnet.

• Berechne den Anteil der p-Werte, die kleiner als das significance-Niveau sind. Dies ist die im Attribut power des Ergebnisobjekts aufgezeichnete Power.

Angenommen, significance ist ein Array der Form shape1, die Elemente von kwargs und n_observations sind gegenseitig auf die Form shape2 broadcastbar und test gibt ein Array von p-Werten der Form shape3 zurück. Dann wird das Attribut power des Ergebnisobjekts die Form shape1 + shape2 + shape3 haben, und das Attribut pvalues wird die Form shape2 + shape3 + (n_resamples,) haben.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Angenommen, wir möchten die Power des t-Tests für unabhängige Stichproben unter den folgenden Bedingungen simulieren:

• Die erste Stichprobe hat 10 Beobachtungen, die aus einer Normalverteilung mit Mittelwert 0 gezogen wurden.

• Die zweite Stichprobe hat 12 Beobachtungen, die aus einer Normalverteilung mit Mittelwert 1.0 gezogen wurden.

• Die Schwelle für p-Werte zur Signifikanz beträgt 0.05.

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>>
>>> test = stats.ttest_ind
>>> n_observations = (10, 12)
>>> rvs1 = rng.normal
>>> rvs2 = lambda size: rng.normal(loc=1, size=size)
>>> rvs = (rvs1, rvs2)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> res.power
0.6116

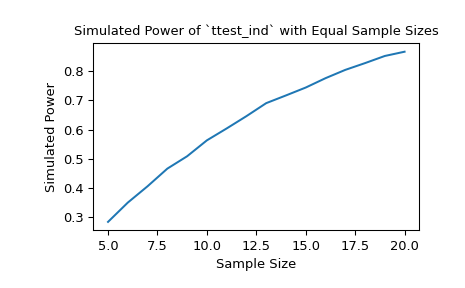
Mit Stichproben der Größen 10 bzw. 12 ist die Power des t-Tests bei einem Signifikanzschwellenwert von 0.05 unter der gewählten Alternative ungefähr 60%. Wir können die Auswirkung der Stichprobengröße auf die Power untersuchen, indem wir Stichprobengrößen-Arrays übergeben.

>>> import matplotlib.pyplot as plt
>>> nobs_x = np.arange(5, 21)
>>> nobs_y = nobs_x
>>> n_observations = (nobs_x, nobs_y)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> ax = plt.subplot()
>>> ax.plot(nobs_x, res.power)
>>> ax.set_xlabel('Sample Size')
>>> ax.set_ylabel('Simulated Power')
>>> ax.set_title('Simulated Power of `ttest_ind` with Equal Sample Sizes')
>>> plt.show()

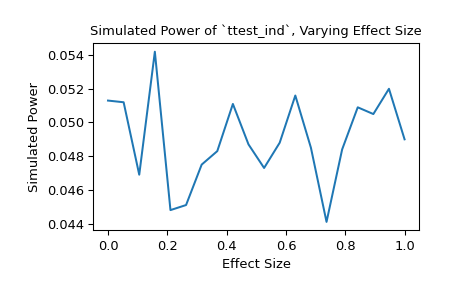
Alternativ können wir den Einfluss der Effektgröße auf die Power untersuchen. In diesem Fall ist die Effektgröße der Ort der Verteilung, die der zweiten Stichprobe zugrunde liegt.

>>> n_observations = (10, 12)
>>> loc = np.linspace(0, 1, 20)
>>> rvs2 = lambda size, loc: rng.normal(loc=loc, size=size)
>>> rvs = (rvs1, rvs2)
>>> res = stats.power(test, rvs, n_observations, significance=0.05,
...                   kwargs={'loc': loc})
>>> ax = plt.subplot()
>>> ax.plot(loc, res.power)
>>> ax.set_xlabel('Effect Size')
>>> ax.set_ylabel('Simulated Power')
>>> ax.set_title('Simulated Power of `ttest_ind`, Varying Effect Size')
>>> plt.show()

Wir können power auch verwenden, um die Typ-I-Fehlerrate (auch als „Größe“ bezeichnet) eines Tests zu schätzen und zu beurteilen, ob sie dem nominalen Niveau entspricht. Zum Beispiel ist die Nullhypothese von jarque_bera, dass die Stichprobe aus einer Verteilung mit derselben Schiefe und Kurtosis wie die Normalverteilung gezogen wurde. Um die Typ-I-Fehlerrate zu schätzen, können wir die Nullhypothese als wahre *alternative* Hypothese betrachten und die Power berechnen.

>>> test = stats.jarque_bera
>>> n_observations = 10
>>> rvs = rng.normal
>>> significance = np.linspace(0.0001, 0.1, 1000)
>>> res = stats.power(test, rvs, n_observations, significance=significance)
>>> size = res.power

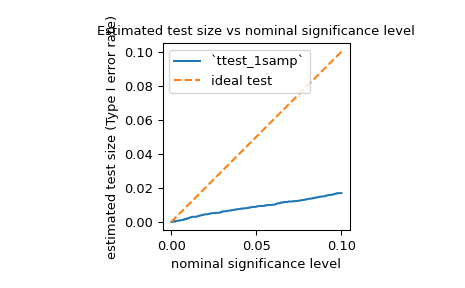
Wie unten gezeigt, liegt die Typ-I-Fehlerrate des Tests für eine so kleine Stichprobe weit unter dem nominalen Niveau, wie in der Dokumentation erwähnt.

>>> ax = plt.subplot()
>>> ax.plot(significance, size)
>>> ax.plot([0, 0.1], [0, 0.1], '--')
>>> ax.set_xlabel('nominal significance level')
>>> ax.set_ylabel('estimated test size (Type I error rate)')
>>> ax.set_title('Estimated test size vs nominal significance level')
>>> ax.set_aspect('equal', 'box')
>>> ax.legend(('`ttest_1samp`', 'ideal test'))
>>> plt.show()

Wie man bei einem so konservativen Test erwarten kann, ist die Power gegenüber einigen Alternativen recht gering. Zum Beispiel ist die Power des Tests unter der Alternative, dass die Stichprobe aus der Laplace-Verteilung gezogen wurde, möglicherweise nicht viel größer als die Typ-I-Fehlerrate.

>>> rvs = rng.laplace
>>> significance = np.linspace(0.0001, 0.1, 1000)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> print(res.power)
0.0587

Dies ist kein Fehler in SciPy's Implementierung; es liegt einfach daran, dass die Nullverteilung der Teststatistik unter der Annahme abgeleitet wird, dass die Stichprobengröße groß ist (d.h. gegen unendlich geht), und diese asymptotische Annäherung für kleine Stichproben nicht genau ist. In solchen Fällen können Resampling- und Monte-Carlo-Methoden (z.B. permutation_test, goodness_of_fit, monte_carlo_test) geeigneter sein.

ZurückIn Tab öffnen