scipy.stats.genhyperbolic

scipy.stats.genhyperbolic = <scipy.stats._continuous_distns.genhyperbolic_gen object>

Eine verallgemeinerte hyperbolische kontinuierliche Zufallsvariable.

Als Instanz der Klasse rv_continuous erbt genhyperbolic von ihr eine Sammlung allgemeiner Methoden (siehe unten für die vollständige Liste) und vervollständigt diese mit Details, die spezifisch für diese Verteilung sind.

Methoden

rvs(p, a, b, loc=0, scale=1, size=1, random_state=None)	Zufallsvariaten.
pdf(x, p, a, b, loc=0, scale=1)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, p, a, b, loc=0, scale=1)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
cdf(x, p, a, b, loc=0, scale=1)	Kumulative Verteilungsfunktion.
logcdf(x, p, a, b, loc=0, scale=1)	Logarithmus der kumulativen Verteilungsfunktion.
sf(x, p, a, b, loc=0, scale=1)	Überlebensfunktion (auch definiert als 1 - cdf, aber sf ist manchmal genauer).
logsf(x, p, a, b, loc=0, scale=1)	Logarithmus der Überlebensfunktion.
ppf(q, p, a, b, loc=0, scale=1)	Perzentilpunktfunktion (Umkehrung von cdf — Perzentile).
isf(q, p, a, b, loc=0, scale=1)	Umgekehrte Überlebensfunktion (Umkehrung von sf).
moment(order, p, a, b, loc=0, scale=1)	Nichtzentrales Moment der angegebenen Ordnung.
stats(p, a, b, loc=0, scale=1, moments=’mv’)	Mittelwert(‚m‘), Varianz(‚v‘), Schiefe(‚s‘) und/oder Kurtosis(‚k‘).
entropy(p, a, b, loc=0, scale=1)	(Differential-)Entropie der RV.
fit(data)	Parameterschätzungen für generische Daten. Siehe scipy.stats.rv_continuous.fit für eine detaillierte Dokumentation der Schlüsselwortargumente.
expect(func, args=(p, a, b), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	Erwartungswert einer Funktion (einer Variablen) bezüglich der Verteilung.
median(p, a, b, loc=0, scale=1)	Median der Verteilung.
mean(p, a, b, loc=0, scale=1)	Mittelwert der Verteilung.
var(p, a, b, loc=0, scale=1)	Varianz der Verteilung.
std(p, a, b, loc=0, scale=1)	Standardabweichung der Verteilung.
interval(confidence, p, a, b, loc=0, scale=1)	Konfidenzintervall mit gleichen Flächen um den Median.

Siehe auch

t, norminvgauss, geninvgauss, laplace, cauchy

Hinweise

Die Wahrscheinlichkeitsdichtefunktion für genhyperbolic ist

\[f(x, p, a, b) = \frac{(a^2 - b^2)^{p/2}} {\sqrt{2\pi}a^{p-1/2} K_p\Big(\sqrt{a^2 - b^2}\Big)} e^{bx} \times \frac{K_{p - 1/2} (a \sqrt{1 + x^2})} {(\sqrt{1 + x^2})^{1/2 - p}}\]

für \(x, p \in ( - \infty; \infty)\), \(|b| < a\), wenn \(p \ge 0\), \(|b| \le a\), wenn \(p < 0\). \(K_{p}(.)\) bezeichnet die modifizierte Bessel-Funktion der zweiten Art und Ordnung \(p\) (scipy.special.kv)

genhyperbolic verwendet p als Schwanzparameter, a als Formparameter und b als Schiefeparameter.

Die obige Wahrscheinlichkeitsdichte ist in „standardisierter“ Form definiert. Zum Verschieben und/oder Skalieren der Verteilung verwenden Sie die Parameter loc und scale. Insbesondere ist genhyperbolic.pdf(x, p, a, b, loc, scale) identisch gleich genhyperbolic.pdf(y, p, a, b) / scale mit y = (x - loc) / scale. Beachten Sie, dass das Verschieben des Ortes einer Verteilung diese nicht zu einer „nicht-zentralen“ Verteilung macht; nicht-zentrale Verallgemeinerungen einiger Verteilungen sind in separaten Klassen verfügbar.

Die ursprüngliche Parametrisierung der Verallgemeinerten Hyperbolischen Verteilung findet sich in [1] wie folgt:

\[f(x, \lambda, \alpha, \beta, \delta, \mu) = \frac{(\gamma/\delta)^\lambda}{\sqrt{2\pi}K_\lambda(\delta \gamma)} e^{\beta (x - \mu)} \times \frac{K_{\lambda - 1/2} (\alpha \sqrt{\delta^2 + (x - \mu)^2})} {(\sqrt{\delta^2 + (x - \mu)^2} / \alpha)^{1/2 - \lambda}}\]

für \(x \in ( - \infty; \infty)\), \(\gamma := \sqrt{\alpha^2 - \beta^2}\), \(\lambda, \mu \in ( - \infty; \infty)\), \(\delta \ge 0, |\beta| < \alpha\), wenn \(\lambda \ge 0\), \(\delta > 0, |\beta| \le \alpha\), wenn \(\lambda < 0\).

Die in SciPy implementierte lage-skalierungsbasierte Parametrisierung basiert auf [2], wobei \(a = \alpha\delta\), \(b = \beta\delta\), \(p = \lambda\), \(scale=\delta\) und \(loc=\mu\) gilt.

Momente werden basierend auf [3] und [4] implementiert.

Für Verteilungen, die ein Spezialfall sind, wie z. B. Student’s t, wird nicht empfohlen, sich auf die Implementierung von genhyperbolic zu verlassen. Um potenzielle numerische Probleme zu vermeiden und aus Leistungsgründen sollten die Methoden der spezifischen Verteilungen verwendet werden.

Referenzen

[1]

O. Barndorff-Nielsen, „Hyperbolic Distributions and Distributions on Hyperbolae“, Scandinavian Journal of Statistics, Bd. 5(3), S. 151-157, 1978. https://www.jstor.org/stable/4615705

[2]

Eberlein E., Prause K. (2002) The Generalized Hyperbolic Model: Financial Derivatives and Risk Measures. In: Geman H., Madan D., Pliska S.R., Vorst T. (Hrsg.) Mathematical Finance - Bachelier Congress 2000. Springer Finance. Springer, Berlin, Heidelberg. DOI:10.1007/978-3-662-12429-1_12

[3]

Scott, David J, Würtz, Diethelm, Dong, Christine und Tran, Thanh Tam, (2009), Moments of the generalized hyperbolic distribution, MPRA Paper, Universitätsbibliothek München, Deutschland, https://EconPapers.repec.org/RePEc:pra:mprapa:19081.

[4]

E. Eberlein und E. A. von Hammerstein. Generalized hyperbolic and inverse Gaussian distributions: Limiting cases and approximation of processes. FDM Preprint 80, April 2003. Universität Freiburg. https://freidok.uni-freiburg.de/fedora/objects/freidok:7974/datastreams/FILE1/content

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy.stats import genhyperbolic
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

Ermitteln Sie den Träger (Support)

>>> p, a, b = 0.5, 1.5, -0.5
>>> lb, ub = genhyperbolic.support(p, a, b)

Berechnen Sie die ersten vier Momente

>>> mean, var, skew, kurt = genhyperbolic.stats(p, a, b, moments='mvsk')

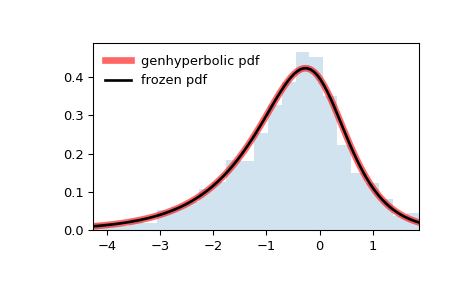
Zeigen Sie die Wahrscheinlichkeitsdichtefunktion (pdf) an

>>> x = np.linspace(genhyperbolic.ppf(0.01, p, a, b),
...                 genhyperbolic.ppf(0.99, p, a, b), 100)
>>> ax.plot(x, genhyperbolic.pdf(x, p, a, b),
...        'r-', lw=5, alpha=0.6, label='genhyperbolic pdf')

Alternativ kann das Verteilungsobjekt (als Funktion) aufgerufen werden, um die Form-, Orts- und Skalierungsparameter festzulegen. Dies gibt ein „eingefrorenes“ RV-Objekt zurück, das die angegebenen Parameter beibehält.

Frieren Sie die Verteilung ein und zeigen Sie die eingefrorene pdf an

>>> rv = genhyperbolic(p, a, b)
>>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')

Überprüfen Sie die Genauigkeit von cdf und ppf

>>> vals = genhyperbolic.ppf([0.001, 0.5, 0.999], p, a, b)
>>> np.allclose([0.001, 0.5, 0.999], genhyperbolic.cdf(vals, p, a, b))
True

Generieren Sie Zufallszahlen

>>> r = genhyperbolic.rvs(p, a, b, size=1000)

Und vergleichen Sie das Histogramm

>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2)
>>> ax.set_xlim([x[0], x[-1]])
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

ZurückIn Tab öffnen