Bartlett-Test auf gleiche Varianzen#
In [1] wurde der Einfluss von Vitamin C auf das Zahnwachstum von Meerschweinchen untersucht. In einer Kontrollstudie wurden 60 Probanden in Gruppen mit geringer, mittlerer und hoher Dosis eingeteilt, die täglich 0,5, 1,0 bzw. 2,0 mg Vitamin C erhielten. Nach 42 Tagen wurde das Zahnwachstum gemessen.
Die unten aufgeführten Arrays small_dose, medium_dose und large_dose erfassen die Zahnwachstumsmessungen der drei Gruppen in Mikrometern.
import numpy as np
small_dose = np.array([
4.2, 11.5, 7.3, 5.8, 6.4, 10, 11.2, 11.2, 5.2, 7,
15.2, 21.5, 17.6, 9.7, 14.5, 10, 8.2, 9.4, 16.5, 9.7
])
medium_dose = np.array([
16.5, 16.5, 15.2, 17.3, 22.5, 17.3, 13.6, 14.5, 18.8, 15.5,
19.7, 23.3, 23.6, 26.4, 20, 25.2, 25.8, 21.2, 14.5, 27.3
])
large_dose = np.array([
23.6, 18.5, 33.9, 25.5, 26.4, 32.5, 26.7, 21.5, 23.3, 29.5,
25.5, 26.4, 22.4, 24.5, 24.8, 30.9, 26.4, 27.3, 29.4, 23
])
Die Statistik scipy.stats.bartlett ist empfindlich für Unterschiede in den Varianzen zwischen den Stichproben.
from scipy import stats
res = stats.bartlett(small_dose, medium_dose, large_dose)
res.statistic
np.float64(0.6654670663030519)
Der Wert der Statistik tendiert dazu, hoch zu sein, wenn es einen großen Unterschied in den Varianzen gibt.
Wir können auf Ungleichheit der Varianzen unter den Gruppen testen, indem wir den beobachteten Wert der Statistik mit der Nullverteilung vergleichen: der Verteilung von Statistikwerten, die unter der Nullhypothese abgeleitet werden, dass die Populationsvarianzen der drei Gruppen gleich sind.
Für diesen Test folgt die Nullverteilung der Chi-Quadrat-Verteilung, wie unten gezeigt.
import matplotlib.pyplot as plt
k = 3 # number of samples
dist = dist = stats.chi2(df=k-1)
val = np.linspace(0, 5, 100)
pdf = dist.pdf(val)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(val, pdf, color='C0')
ax.set_title("Bartlett Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
ax.set_xlim(0, 5)
ax.set_ylim(0, 1)
plot(ax)
plt.show()
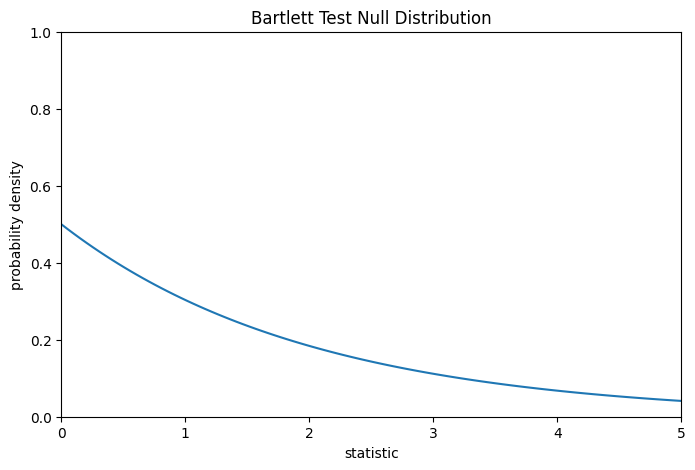
Der Vergleich wird durch den p-Wert quantifiziert: der Anteil der Werte in der Nullverteilung, die größer oder gleich dem beobachteten Wert der Statistik sind.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.3f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (1.5, 0.22), (2.25, 0.3), arrowprops=props)
i = val >= res.statistic
ax.fill_between(val[i], y1=0, y2=pdf[i], color='C0')
plt.show()
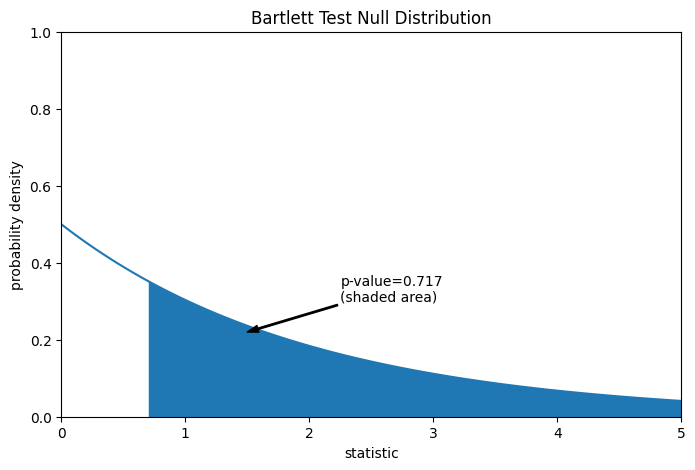
res.pvalue
np.float64(0.71696121509966)
Wenn der p-Wert „klein“ ist – das heißt, wenn die Wahrscheinlichkeit gering ist, Daten aus Verteilungen mit identischen Varianzen zu ziehen, die einen so extremen Wert der Statistik erzeugen – kann dies als Beweis gegen die Nullhypothese zugunsten der Alternative genommen werden: Die Varianzen der Gruppen sind nicht gleich. Beachten Sie, dass
Das Umgekehrte gilt nicht; d.h. der Test wird nicht verwendet, um Beweise für die Nullhypothese zu liefern.
Der Schwellenwert für Werte, die als „klein“ gelten, ist eine Wahl, die vor der Analyse der Daten getroffen werden sollte [2] und die Risiken von sowohl falsch positiven Ergebnissen (fälschliche Ablehnung der Nullhypothese) als auch falsch negativen Ergebnissen (Nichtablehnung einer falschen Nullhypothese) berücksichtigt.
Kleine p-Werte sind kein Beweis für einen *großen* Effekt; sie können nur einen Beweis für einen „signifikanten“ Effekt liefern, was bedeutet, dass sie unter der Nullhypothese unwahrscheinlich aufgetreten wären.
Beachten Sie, dass die Chi-Quadrat-Verteilung die Nullverteilung liefert, wenn die Beobachtungen normalverteilt sind. Für kleine Stichproben, die aus nicht-normalverteilten Populationen gezogen werden, kann es geeigneter sein, einen Permutationstest durchzuführen: Unter der Nullhypothese, dass alle drei Stichproben aus derselben Population stammen, ist jede der Messungen gleich wahrscheinlich in jeder der drei Stichproben beobachtet worden. Daher können wir eine randomisierte Nullverteilung bilden, indem wir die Statistik unter vielen zufällig generierten Partitionierungen der Beobachtungen in die drei Stichproben berechnen.
def statistic(*samples):
return stats.bartlett(*samples).statistic
ref = stats.permutation_test(
(small_dose, medium_dose, large_dose), statistic,
permutation_type='independent', alternative='greater'
)
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
bins = np.linspace(0, 5, 25)
ax.hist(
ref.null_distribution, bins=bins, density=True, facecolor="C1"
)
ax.legend(['asymptotic approximation\n(many observations)',
'randomized null distribution'])
plot(ax)
plt.show()
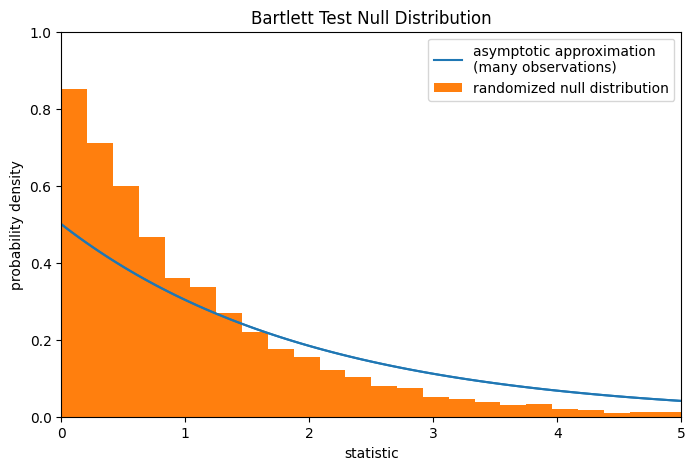
ref.pvalue # randomized test p-value
np.float64(0.5362)
Beachten Sie, dass es erhebliche Diskrepanzen zwischen dem hier berechneten p-Wert und der asymptotischen Näherung gibt, die von scipy.stats.bartlett oben zurückgegeben wird. Die statistischen Schlussfolgerungen, die rigoros aus einem Permutationstest gezogen werden können, sind begrenzt; nichtsdestotrotz können sie in vielen Fällen der bevorzugte Ansatz sein [3].