Jarque-Bera Güte der Anpassungstest#
Angenommen, wir möchten anhand von Messungen schließen, ob die Gewichte erwachsener männlicher Personen in einer medizinischen Studie nicht normalverteilt sind [1]. Die Gewichte (Pfund) sind im folgenden Array x aufgeführt.
import numpy as np
x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])
Der Jarque-Bera-Test scipy.stats.jarque_bera beginnt mit der Berechnung einer Statistik, die auf der Schiefe und Kurtosis der Stichprobe basiert.
from scipy import stats
res = stats.jarque_bera(x)
res.statistic
np.float64(6.982848237344646)
Da die Normalverteilung eine Schiefe von Null und eine Kurtosis von Null ("Exzess" oder "Fisher") hat, ist der Wert dieser Statistik für Stichproben, die aus einer Normalverteilung gezogen wurden, tendenziell niedrig.
Der Test wird durchgeführt, indem der beobachtete Wert der Statistik mit der Nullverteilung verglichen wird: der Verteilung von Statistikwerten, die unter der Nullhypothese abgeleitet wurden, dass die Gewichte aus einer Normalverteilung stammen.
Für den Jarque-Bera-Test ist die Nullverteilung für sehr große Stichproben die Chi-Quadrat-Verteilung mit zwei Freiheitsgraden.
import matplotlib.pyplot as plt
dist = stats.chi2(df=2)
jb_val = np.linspace(0, 11, 100)
pdf = dist.pdf(jb_val)
fig, ax = plt.subplots(figsize=(8, 5))
def jb_plot(ax): # we'll reuse this
ax.plot(jb_val, pdf)
ax.set_title("Jarque-Bera Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
jb_plot(ax)
plt.show();
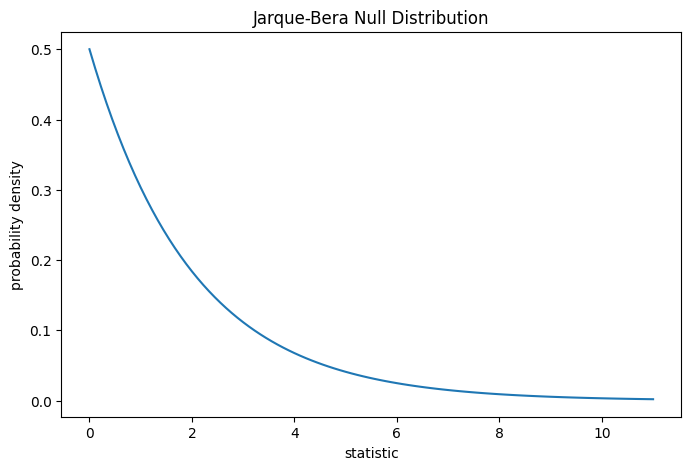
Der Vergleich wird durch den p-Wert quantifiziert: der Anteil der Werte in der Nullverteilung, die größer oder gleich dem beobachteten Wert der Statistik sind.
fig, ax = plt.subplots(figsize=(8, 5))
jb_plot(ax)
pvalue = dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.6f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (7.5, 0.01), (8, 0.05), arrowprops=props)
i = jb_val >= res.statistic # indices of more extreme statistic values
ax.fill_between(jb_val[i], y1=0, y2=pdf[i])
ax.set_xlim(0, 11)
ax.set_ylim(0, 0.3)
plt.show()
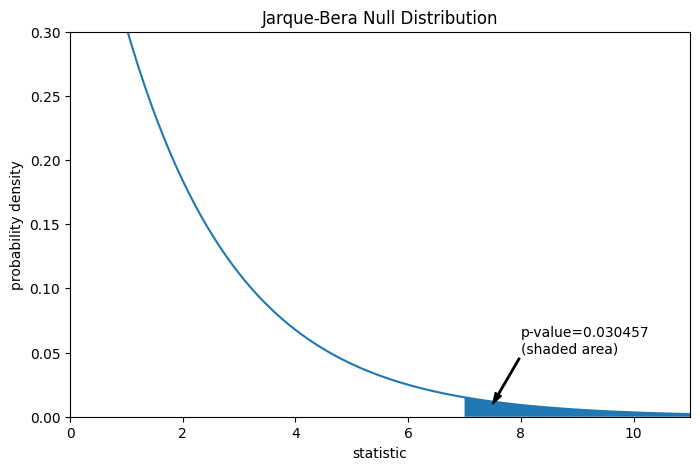
res.pvalue
np.float64(0.03045746622458189)
Wenn der p-Wert "klein" ist - d.h. wenn die Wahrscheinlichkeit gering ist, aus einer normalverteilten Population Daten zu ziehen, die einen derart extremen Wert der Statistik erzeugen -, kann dies als Hinweis gegen die Nullhypothese zugunsten der Alternativhypothese gewertet werden: die Gewichte wurden nicht aus einer Normalverteilung gezogen. Beachten Sie, dass
Das Umgekehrte gilt nicht; d.h. der Test wird nicht verwendet, um Beweise für die Nullhypothese zu liefern.
Der Schwellenwert für Werte, die als „klein“ gelten, ist eine Wahl, die vor der Analyse der Daten getroffen werden sollte [2] und die Risiken von sowohl falsch positiven Ergebnissen (fälschliche Ablehnung der Nullhypothese) als auch falsch negativen Ergebnissen (Nichtablehnung einer falschen Nullhypothese) berücksichtigt.
Beachten Sie, dass die Chi-Quadrat-Verteilung eine asymptotische Annäherung der Nullverteilung darstellt; sie ist nur für Stichproben mit vielen Beobachtungen genau. Für kleine Stichproben wie unsere kann scipy.stats.monte_carlo_test eine genauere, wenn auch stochastische, Annäherung des exakten p-Wertes liefern.
def statistic(x, axis):
# underlying calculation of the Jarque Bera statistic
s = stats.skew(x, axis=axis)
k = stats.kurtosis(x, axis=axis)
return x.shape[axis]/6 * (s**2 + k**2/4)
res = stats.monte_carlo_test(x, stats.norm.rvs, statistic,
alternative='greater')
fig, ax = plt.subplots(figsize=(8, 5))
jb_plot(ax)
ax.hist(res.null_distribution, np.linspace(0, 10, 50),
density=True)
ax.legend(['asymptotic approximation (many observations)',
'Monte Carlo approximation (11 observations)'])
plt.show()
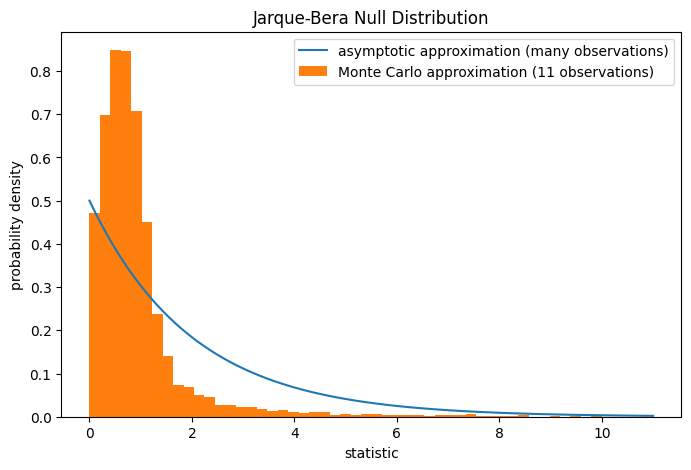
res.pvalue
np.float64(0.0095)
Darüber hinaus können, trotz ihrer stochastischen Natur, auf diese Weise berechnete p-Werte verwendet werden, um die Rate von falschen Ablehnungen der Nullhypothese exakt zu kontrollieren [3].