Kendalls tau-Test#
Kendalls tau ist ein Maß für die Übereinstimmung zwischen zwei Rangfolgen.
Betrachten Sie die folgenden Daten aus [1], die die Beziehung zwischen freiem Prolin (einer Aminosäure) und Gesamtcollagen (einem Protein, das häufig in Bindegewebe vorkommt) in ungesunden menschlichen Lebern untersuchten.
Die unten aufgeführten Arrays x und y erfassen Messungen der beiden Verbindungen. Die Beobachtungen sind gepaart: Jede Messung des freien Prolins wurde aus derselben Leber wie die Messung des Gesamt kollagens am selben Index entnommen.
import numpy as np
# total collagen (mg/g dry weight of liver)
x = np.array([7.1, 7.1, 7.2, 8.3, 9.4, 10.5, 11.4])
# free proline (μ mole/g dry weight of liver)
y = np.array([2.8, 2.9, 2.8, 2.6, 3.5, 4.6, 5.0])
Diese Daten wurden in [2] mithilfe des Spearman-Korrelationskoeffizienten analysiert, einer Statistik, die Kendalls tau ähnelt, da sie ebenfalls empfindlich auf ordinale Korrelationen zwischen den Stichproben reagiert. Führen wir eine analoge Studie mit Kendalls tau durch.
from scipy import stats
res = stats.kendalltau(x, y)
res.statistic
np.float64(0.5499999999999999)
Der Wert dieser Statistik ist tendenziell hoch (nahe 1) für Stichproben mit einer stark positiven ordinalen Korrelation, niedrig (nahe -1) für Stichproben mit einer stark negativen ordinalen Korrelation und gering in der Betragshöhe (nahe Null) für Stichproben mit schwacher ordinaler Korrelation.
Der Test wird durchgeführt, indem der beobachtete Wert der Statistik mit der Nullverteilung verglichen wird: der Verteilung von Statistikwerten, die unter der Nullhypothese abgeleitet werden, dass Gesamtcollagen und Messungen von freiem Prolin unabhängig sind.
Für diesen Test wird die Nullverteilung für große Stichproben ohne Bindungen als Normalverteilung mit der Varianz (2*(2*n + 5))/(9*n*(n - 1)) angenähert, wobei n = len(x).
import matplotlib.pyplot as plt
n = len(x) # len(x) == len(y)
var = (2*(2*n + 5))/(9*n*(n - 1))
dist = stats.norm(scale=np.sqrt(var))
z_vals = np.linspace(-1.25, 1.25, 100)
pdf = dist.pdf(z_vals)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(z_vals, pdf)
ax.set_title("Kendall Tau Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
Der Vergleich wird durch den p-Wert quantifiziert: dem Anteil der Werte in der Nullverteilung, die so extrem oder extremer sind als der beobachtete Wert der Statistik. Bei einem zweiseitigen Test, bei dem die Statistik positiv ist, werden sowohl die Elemente der Nullverteilung, die größer als die transformierte Statistik sind, als auch die Elemente der Nullverteilung, die kleiner als das Negative des beobachteten Statistikwerts sind, als "extremer" betrachtet.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.cdf(-res.statistic) + dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (0.65, 0.15), (0.8, 0.3), arrowprops=props)
i = z_vals >= res.statistic
ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
i = z_vals <= -res.statistic
ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(-1.25, 1.25)
ax.set_ylim(0, 0.5)
plt.show()
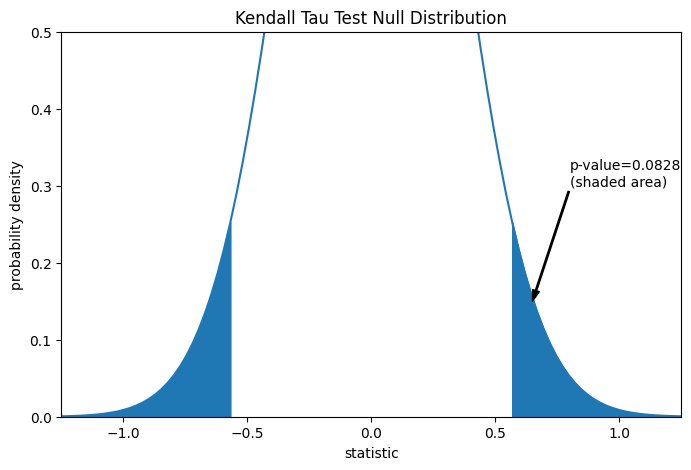
res.pvalue
np.float64(0.09108705741631495)
Beachten Sie, dass es geringfügige Abweichungen zwischen dem schattierten Bereich der Kurve und dem von scipy.stats.kendalltau zurückgegebenen p-Wert gibt. Dies liegt daran, dass unsere Daten Bindungen aufweisen und wir eine Bindungskorrektur der Varianz der Nullverteilung vernachlässigt haben, die scipy.stats.kendalltau durchführt. Für Stichproben ohne Bindungen würden die schattierten Bereiche unseres Diagramms und der von scipy.stats.kendalltau zurückgegebene p-Wert exakt übereinstimmen.
Wenn der p-Wert „klein“ ist – das heißt, wenn die Wahrscheinlichkeit, Daten aus unabhängigen Verteilungen zu ziehen, die einen so extremen Wert der Statistik ergeben, gering ist – kann dies als Beweis gegen die Nullhypothese zugunsten der Alternativhypothese gewertet werden: Die Verteilung von Gesamtcollagen und freiem Prolin sind *nicht* unabhängig. Beachten Sie, dass
Das Umgekehrte gilt nicht; d.h. der Test wird nicht verwendet, um Beweise für die Nullhypothese zu liefern.
Der Schwellenwert für Werte, die als "klein" gelten, ist eine Wahl, die getroffen werden sollte, bevor die Daten analysiert werden [3], wobei die Risiken von sowohl falsch positiven Ergebnissen (fälschliches Ablehnen der Nullhypothese) als auch falsch negativen Ergebnissen (Nichtablehnen einer falschen Nullhypothese) berücksichtigt werden.
Kleine p-Werte sind kein Beweis für einen *großen* Effekt; sie können nur einen Beweis für einen „signifikanten“ Effekt liefern, was bedeutet, dass sie unter der Nullhypothese unwahrscheinlich aufgetreten wären.
Für Stichproben ohne Bindungen von moderater Größe kann scipy.stats.kendalltau den p-Wert exakt berechnen. In Anwesenheit von Bindungen greift scipy.stats.kendalltau jedoch auf eine asymptotische Approximation zurück. Dennoch können wir einen Permutationstest verwenden, um die Nullverteilung exakt zu berechnen: Unter der Nullhypothese, dass Gesamtcollagen und freies Prolin unabhängig sind, war jede der Messungen von freiem Prolin gleich wahrscheinlich mit jeder der Messungen von Gesamtcollagen beobachtet worden. Daher können wir eine *exakte* Nullverteilung bilden, indem wir die Statistik unter jeder möglichen Paarung von Elementen zwischen x und y berechnen.
def statistic(x): # explore all possible pairings by permuting `x`
return stats.kendalltau(x, y).statistic # ignore pvalue
ref = stats.permutation_test((x,), statistic,
permutation_type='pairings')
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
bins = np.linspace(-1.25, 1.25, 25)
ax.hist(ref.null_distribution, bins=bins, density=True)
ax.legend(['asymptotic approximation\n(many observations)',
'exact null distribution'])
plot(ax)
plt.show()
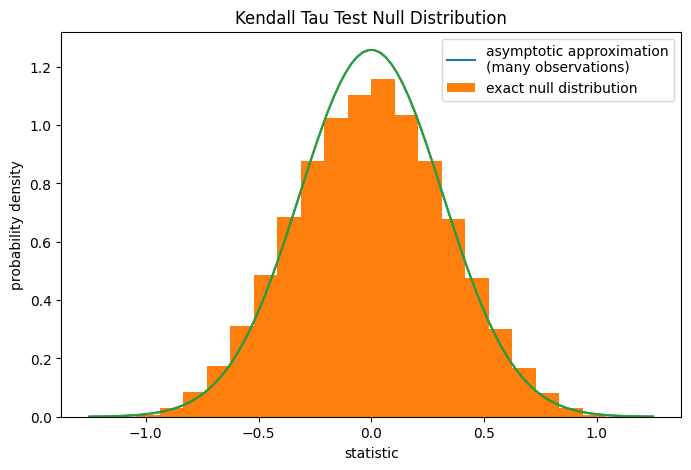
ref.pvalue
np.float64(0.12222222222222222)
Beachten Sie, dass es erhebliche Abweichungen zwischen dem hier berechneten exakten p-Wert und der oben von scipy.stats.kendalltau zurückgegebenen Approximation gibt. Bei kleinen Stichproben mit Bindungen sollten für genauere Ergebnisse ein Permutationstest durchgeführt werden.